非饱和土大气张力通用公式与地基渗流固结沉降

蒙理明

（海口市建设工程质量安全监督站，海口 570206）

非饱和土大气张力通用公式与地基渗流固结沉降

蒙理明

（海口市建设工程质量安全监督站，海口 570206）

提出了“地基渗流固结理论应该用超自由水压力的等效压缩系数来描述，地基沉降应该用总附加应力及总应力压缩模量来计算，都不需要有效应力”；用超自由水压力的等效压缩系数修正了太沙基一维固结微分方程；初步探讨了非饱和土的等效压缩系数和等效压缩模量。

等效压缩系数； 等效压缩模量； 地基渗流固结

用非饱和土大气张力通用公式的观点探讨地基渗流固结沉降，其依据有：

见文献［1］的108至111页，太沙基一维渗流固结理论需作如下假设：土是均质的，完全饱和的；土粒和水是不可压缩的；土层的压缩和土中水的渗流只沿竖向发生，是一维的；土中水的渗流服从达西定律，且渗透系数k保持不变；孔隙比的变化与有效应力的变化成正比，即－e／dσ＇＝α，且压缩系数ɑ保持不变；外荷载是一次瞬时施加的。

先推出

等等，然后得：

太沙基一维固结微分方程

其中，e为孔隙比；t为时间；u为自由水压力；α为土的压缩系数

土的竖向固结系数

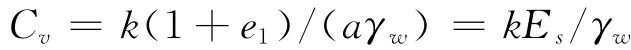
其中，k为渗透系数；e1为初始孔隙比；γw为水的重度；Es为土的压缩模量。

然后，求出土层单面排水和双面排水的解u（z，t），其中，时间因数H为孔隙水的最大渗径，在单面排水下为土层厚度。

见文献［2］，提出了：土的压缩变形的变化只取决于有效应力的变化的观点是不成立的。自由水和孔隙气同样具有抗压能力，地基压缩变形应该用总应力计算。有效应力的实质是自由水和孔隙气没有抗剪能力。还提出了：自由水和孔隙气渗流时同样具有抗压能力，具有“等效压缩模量”，与总应力压缩模量曲线相似，主导了地基土的压缩变形。

1 饱和土渗流固结实际的三个压缩系数

见图1，是常规的压缩系数，见文献［1］86页，室内侧限压缩试验，常规压缩试验的加荷等级P为：50 kPa、100kPa、200kPa、300kPa、400kPa，每一级荷载要求恒压24h或当在1h内的压缩量不超过0.005 mm时，认为变形已经稳定，并测定稳定时的总压缩量ΔH，并根据ΔH求出相应的孔隙比。对于饱和土渗流固结，取P1与P2靠近一次瞬时施加的外荷载的范围，规定土的总应力压缩系数α＝tgα＝（e1－e2）／（P2－P1）。

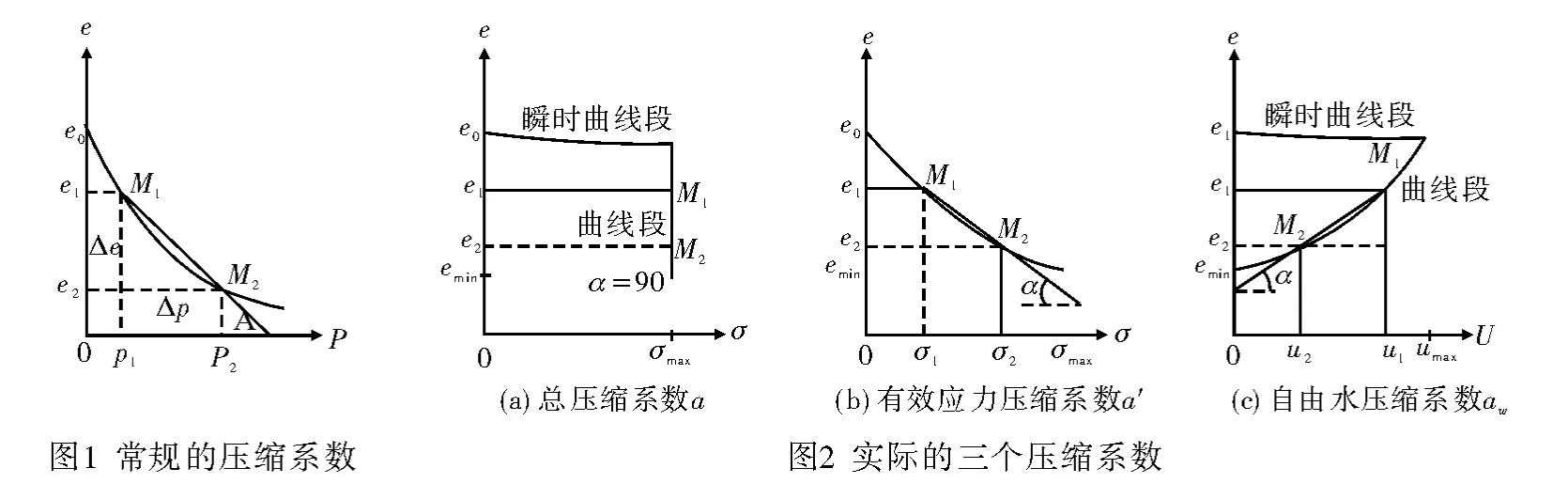
见图2，是实际的三个压缩系数，包括总应力、有效应力、自由水的压缩系数。σ、σ＇、u是一次加载产生的附加应力和超自由水压力，不包括初始应力和初始自由水压力。应该注意的是，孔隙比、总应力、自由水压力（通常说的孔隙水压力）是可以在试验中测得的。而有效应力通过总应力和自由水压力计算得到。

首先是总应力压缩系数，见图2（a），初始孔隙比为e0，瞬时加荷，总附加应力由零迅速增加到σmax，但土体压密很少，孔隙比很少变化，形成瞬时曲线段，α≈0°；接着σmax保持不变，土体不断压密，孔隙比变小到emin稳定，形成直线段，α≈90°。压缩系数为：瞬时曲线段的ɑ＝0和直线段ɑ＝∞。

其次是超自由水压力的等效压缩系数ɑw，见图2（c），初始孔隙比为e0，瞬时加荷，超自由水压力由零迅速增加到umax，但土体压密很少，孔隙比很少变化，形成瞬时曲线段，α≈0°；接着umax逐渐消散为零，土体不断压密，孔隙比变小到emin稳定，形成曲线段，0°＜ɑ＜90°，为一变量。压缩系数为：瞬时曲线段的ɑw＝0和曲线段ɑw＝tgα。

最后是有效应力压缩系数ɑ＇，见图2（b），要先由总附加应力和超自由水压力计算，先得到附加的有效应力，才能绘制。随着孔隙比不断变小，或者说超自由水压力的不断消散，附加有效应力由零增加到σ＇max，0°＜ɑs＜90°，为一变量。压缩系数为：ɑ＇＝tgα。

三个压缩系数可以独立存在，相同之处为，都对应土的孔隙比e，不同之处为，分别对应总附加应力、附加有效应力、超自由水压力。很显然，真实反映并能够直接应用于一维渗流固结理论的是，超自由水压力的等效压缩系数ɑw。

2 用超自由水压力的等效压缩系数修正太沙基一维固结微分方程

2.1 用超自由水压力的等效压缩系数修正太沙基一维固结微分方程

见图2（c），很显然，de／du＝ɑw设ɑw为常数（如取其平均值）

其中，土的竖向固结系数Cv＝k（1＋e1）／（ɑwγw）

然后，求出土层单面排水和双面排水的解u（z，t），其中，时间因数H为孔隙水的最大渗径，在单面排水下为土层厚度。

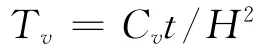
式（2.1）为用超自由水压力的等效压缩系数修正的太沙基一维固结微分方程，不同之处为，用超自由水压力的等效压缩系数ɑw代替了规定的总应力压缩系数α。

2.2 太沙基一维渗流固结理论的不妥之处

造成不妥的原因是，太沙基一维固结理论，一开始就设定了－de／dσ＇＝ɑ，即有效应力原理，而又用了与有效应力不对应的常规的总应力压缩系数ɑ。归根结底在于，“土的压缩变形的变化只取决于有效应力的变化”的观点是不成立的。

3 饱和土渗流固结的三个独立的压缩模量及应用

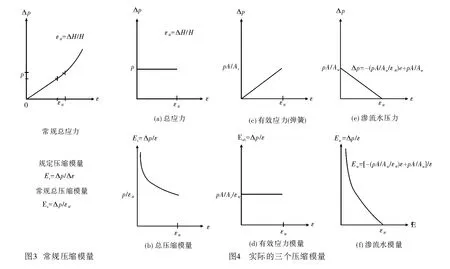
见图3，是常规的压缩模量。见文献［1］86页，常规压缩试验的加荷等级P为：50kPa、100kPa、200kPa、300kPa、400kPa，每一级荷载要求恒压24h或当在1h内的压缩量不超过0.005mm时，认为变形已经稳定，并测定稳定时的总压缩量ΔH，Δε＝ΔHi／H。对于饱和土渗流固结，取Δp＝p等于一次瞬时施加的外荷载，其对应的Δε＝εH＝ΔH／H，规定土的总应力压缩模量Es＝p／εH。

见图4，来自文献［2］，是弹簧活塞模型中，实际的三个压缩模量，包括总应力、有效应力、渗流（自由）水的压缩模量。假设Δp为直线变化。Δp是一次加载产生的附加应力或超自由水压力，不包括初始应力和初始自由水压力。

下标s0、w分别代表弹簧和水。水的初始高度为H，弹簧的截面积为As，水的截面积为Aw，总面积为A。见图4（a），活塞瞬时加压总应力增量p时，见图4（e），超自由水压应力为pw＝pA／Aw；总应力增量p保持不变，活塞下降高度ΔH后稳定，即压缩应变为εH＝ΔH／H时，超静自由水压力消散为零，见图4（c），弹簧受到的压应力由零增加为ps0＝pA／As。

实际的三个压缩模量见图4（b）～图4（f）。首先图4（b），总应力压缩模量Es，图中是一条双曲线函数Es＝p／ε，活塞瞬时加压总应力增量p时，Es为∞，总应力增量p保持不变，到应变稳定为εH＝ΔH／H时，Es＝p／εH，即总应力压缩模量的下界，等于图3的常规总应力压缩模量。其次是图4（d），有效应力的压缩模量，是一常量Es0＝pA／As／εH，实际土颗粒结构在压缩过程中，不断压密或错位压密，Es0是不断变大的，不是常量。但不论如何，弹簧的压缩模量曲线与总应力压缩模量曲线在整个压缩过程中基本没有什么相似之处。最后是f，自由水的“等效压缩模量”，也是一条双曲线Ew＝－pA／Aw／εH＋pA／Aw／ε，与总应力压缩模量曲线相似：活塞瞬时加压总应力增量p时，Ew为∞，并逐渐衰减；但到应变稳定为εH＝ΔH／H时，超自由水压力消散为零，即渗流水已经不分担总应力增量，Ew＝0。

渗流水既然有刚度（等效压缩模量）就必然参与抵抗压缩变形。但总应力压缩模量曲线与渗流水的“等效压缩模量”曲线相似，却也不完全等同，说明总应力的刚度由自由水和土颗粒进行变形协同工作形成，所以用有效应力来对应总应力压缩模量进行地基沉降计算是错误的。这样，文献［1］的99页的例题5－1，用分层总和法求基础中点的沉降量，自重应力在地下水位以下取有效重度进行计算是错误的，应该用总天然重度。

三个压缩模量可以独立存在，相同之处，都对应土的压缩应变ε，不同之处为，分别对应总附加应力、附加有效应力、超自由水压力。由于总附加应力p在试验中是根据实际工况直接设定的，与其对应的总应力压缩模量Es在试验中直接得到，所以，能真实反映实际工况并能够直接用于地基沉降计算。见文献［3］的5.3.5条，我国规范就是用的总附加应力p对应总应力压缩模量Es计算地基沉降。只不过，取压缩模量Esi时，土的自重应力不应按有效自重应力计算。所以，地基沉降计算也不需要有效应力。

4 再论“土的压缩变形的变化只取决于有效应力的变化的观点是不成立的”

上述地基渗流固结理论的描述和地基沉降的计算都不需要有效应力，证明了经典有效应力原理关于“土的压缩变形的变化只取决于有效应力的变化”的观点是不成立的。

经典有效应力原理关于地基压缩变形的部分在应用中常遇到困难。见文献［4］的120页，“需要说明的是，孔隙水应力等于孔隙静水应力与超静水应力之和。孔隙静水应力是由孔隙水的自重产生的，在地下水位不变的条件下，孔隙静水应力不随时间变化，对土骨架的应力和变形不产生影响。孔隙超静水应力是指由外荷载和其他因素产生的超出静水水位的那部分应力，随着土中渗流的产生，超静水应力随时间而变化，并对土骨架的应力和变形产生影响。”

但是这段话并不能让经典有效应力原理摆脱困难，反而是承认“孔隙水压力的变化对土骨架的应力和变形产生影响，土的压缩变形的变化只取决于有效应力的变化的观点是不成立的”。同样可以说：“在地基渗流固结问题上，有效应力由初始有效应力（有效自重应力）和附加有效应力组成。初始有效应力是常量，对土骨架的应力和变形不产生影响，附加有效应力随时间而变化，并对土骨架的应力和变形产生影响。”在这里，自由水压力和有效应力是同等地位的。所以，更准确的结论是“超自由水压力和附加有效应力都会对土骨架的应力和变形产生影响，土的压缩变形的变化只取决于有效应力的变化的观点是不成立的。”

举个通俗的例子：在装有较多水的玻璃瓶里浮着一个木块，用指头外下压它，它会下沉，这是有效应力发生了变化，但并非施加有效应力木块才会往下沉。在玻璃瓶底钻个小孔，木块会随着水的渗流下沉，这提示饱和土中错位后浮于水中的颗粒会随着自由水的渗流而下沉。另外，玻璃瓶里如果是砂粒，不用钻孔就会下沉，下沉过程中，作用于砂粒的有效应力，即重力减去浮力（所排开的同体积水的重量）始终没有变，这提示饱和土中错位后较重的颗粒会自动下沉。下沉的漂浮颗粒或砂粒，主要受到水压力的作用，这些断断续续的过程对时间的积分就是地基的一部分沉降，而这些过程主要取决于自由水压力，而不是有效应力。

5 非饱和土渗流固结的压缩模量和压缩系数初探

见文献［5］摘要：拟将非饱和土受压后的固结过程简单地分为压密和固结两个阶段。在压密过程中，与饱和土固结不同的是，由于非饱和土的孔隙水、气来不及排出，与骨架共同承担荷载，产生了超孔隙气压和超孔隙水压，这个阶段主要是压缩孔隙气产生的压缩变形；固结阶段，土体在恒定荷载作用下，超孔隙气压和超孔隙水压逐渐消散而固结。

非饱和土渗流固结不能统一为一个模式。天然土层中的支持毛细水带、悬挂毛细水带、角部毛细水带以及人工压实的填土有区别。支持毛细水带、悬挂毛细水带在渗流固结中，除了孔隙气可以排出外，毛细水及颗粒错位后被破坏的部分结合水转化为自由水可以由毛细管排出。而角部毛细水带一般只有孔隙气排出。人工压实的填土，见文献［6］的32页，“试验统计证明：最优含水量Wop与土的塑限Wp有关，大致为Wop＝Wp＋2%。土中粘土矿物含量愈大，则最优含水量愈大。”由于塑限Wp是结合水的界限，所以人工压实的填土基本没有什么自由水，可以参考角部毛细水的渗流固结。但下雨、下雪又无防水措施的情况除外。

下面，以角部毛细水的土层为对象，初步探讨非饱和土渗流固结的压缩模量和压缩系数。由于土的渗流固结理论的描述和地基沉降的计算都不需要有效应力，所以下面不绘制关于有效应力的图示。

5.1 非饱和土渗流固结的压缩模量（角部毛细水）

见图5，是常规的压缩模量，与图3饱和土的常规压缩模量相同。

见图6，是非饱和土渗流固结（角部毛细水）的实际的三个压缩模量。假设Δp为直线变化。Δp是一次加载产生的附加应力、超自由水压力和超孔隙气压力。应该注意的是，应变、总应力、孔隙气压力都可以在试验中测得，而自由水压力不易测得。

见图6（a），一次瞬时加压总应力增量p时，与饱和土不同的是，虽然非饱和土的孔隙水、气来不及排出，但由于孔隙气可压缩，见图6（e）、图6（c），超孔隙气压力逐渐由零增加到最大值ua，超自由水压力也逐渐由零增加到最大值uw，此阶段为压密阶段，压密阶段有一部分压缩变形；然后，总应力增量p保持不变，土体下降到高度ΔH后稳定，即压缩应变增加为εH＝ΔH／H时，超孔隙气压力和超自由水压力消散为零，此阶段为固结阶段。

实际的三个压缩模量见图6（b）～图6（f）。首先是图6（b），总应力压缩模量Es，与图4饱和土的相似，不同之处在于瞬时加载时，由于孔隙气可以压缩，所以土体产生变形的时间早，也较大，所以总应力压缩模量双曲线开始∞部分相对平缓。其次是图6（f），超孔隙气等效压缩模量Ea，由于孔隙气可压缩，所以压密阶段类似弹性体，压缩模量近似为常量。然后，固结阶段为双曲线，体现超孔隙气压力逐渐消散为零的压缩模量特性。最后是图6（d），超自由水压力等效压缩模量Ew，由于角部毛细水是由收缩膜与孔隙气共处的，毛细水可以随孔隙气的压缩及消散变形，所以其压缩模量与超孔隙气的相似。注意的是，自由水不可压缩，所以相对于孔隙气等效刚度较大（见图6（d）、图6（f）），单位自由水比单位孔隙气分配的总应力也较大（见图6（c）、图6（e））。

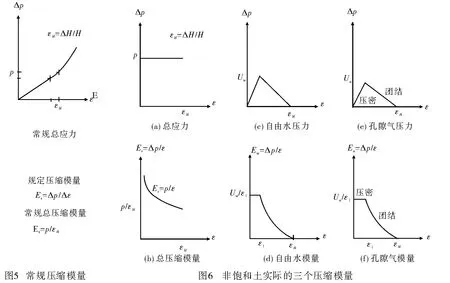
总应力压缩模量曲线与其他两个压缩模量曲线不完全等同，说明总应力的刚度是土颗粒（可包括结合水膜）、自由水、孔隙气还有收缩膜的刚度（或等效刚度）综合构成的。同饱和土一样，真实反映实际工况并能够直接用于地基沉降计算的是，总应力压缩模量Es及与其对应的总应力增量p。

5.2 非饱和土渗流固结的压缩系数（角部毛细水）

见图7，是常规的压缩系数，与图1饱和土的常规压缩系数相同。

见图8，是非饱和土实际的三个压缩系数。σ、u是一次加载产生的附加应力、超自由水压力和超孔隙气压力。孔隙比、总应力、孔隙气压力可以在试验中测得。

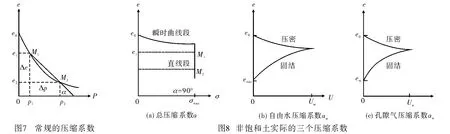
首先是总应力压缩系数ɑ，见图8（a），与图2饱和土的相似，不同之处在于瞬时加载时，由于孔隙气可以压缩，所以孔隙比变小的时间早，也较大，所以总应力压缩系数初始曲线部分不像饱和土那么平缓。其次是超孔隙气的等效压缩系数ɑa，见图8（c），由于孔隙气可压缩，超孔隙气压力逐渐由零增加到最大值ua，且孔隙比也像弹性体那样由初始e0逐渐变小，为压密阶段，然后随着超孔隙气压力的消散，孔隙比再逐渐变为最小值emin并稳定。等效压缩系数ɑa＝tgα，0°＜ɑ＜90°。最后是超自由水压力的等效压缩系数ɑw，见图8（b），由于角部毛细水可以随孔隙气的压缩及消散而变形，且等效刚度较大，所以其压缩系数与超孔隙气的相似，并且uw＞ua。很显然，真实反映并能够直接应用于渗流固结理论的是，超孔隙气压力和超自由水压力的等效压缩系数。

6 结 论

a.用超自由水压力的等效压缩系数修正了太沙基一维固结微分方程，不需要有效应力。

b.真实反映实际工况并能够直接用于地基沉降计算的是，总应力压缩模量及与其对应的总附加应力，也不需要有效应力。

c.土颗粒先柔后刚，自由水先刚后柔，对立统一构成饱和土总刚度，渗流固结完成实现土体更密实的飞跃。孔隙气、自由水既然有刚度（等效压缩模量及等效压缩系数）就必然参与抵抗压缩变形。“土的压缩变形的变化只取决于有效应力的变化”的观点是不成立的。

d.以角部毛细水为例，初步探讨了非饱和土渗流固结的等效压缩模量和等效压缩系数。

［1］高大钊，袁聚云，谢永利.土质学与土力学［M］，第3版.北京：人民交通出版社，2001.

［2］蒙理明.非饱和土大气张力通用公式与地基压缩变形初探［J］.建材世界，2014，35（1）：83－88.

［3］GB 50007—2011.建筑地基基础设计规范［S］.

［4］李艳春，张建新，刘熙媛，等.土质学与土力学［M］.第1版.北京：中国建材工业出版社，2005.

［5］曹雪山，殷宗泽，凌 华.非饱和土受压变形的简化计算研究［J］.岩土工程学报，2008（1）：61－65.

［6］姚仰平，汪仁和，徐新生.土力学［M］.北京：高等教育出版社，2004.

Tension Atmosphere General Formula of Unsaturated Soil and the Foundation Seepage Consolidation Settlement

MENG Li－ming
（Haikou City Construction Engineering Quality Safety Supervise Station，Haikou 570206，China）

This paper put forward“foundation seepage consolidation theory should be described in the equivalent compression coefficient of super free water pressure，foundation settlement should use the total additional stress and total stress compression modulus to calculate，don＇t need effective stress”.The one dimension consolidation differential equation of Terzaghi is corrected with super free water pressure equivalent compression coefficient.And the equivalent compression coefficient and equivalent compression modulus of unsaturated soil are discussed.

the equivalent coefficient of compression； the equivalent modulus of compression； the foundation seepage consolidation

10.3963／j.issn.1674－6066.2014.02.035

2014－02－28.

蒙理明（1955－），教授级高工.E－mail：66229258mlm＠163.com