丝网印刷及表面科学问题探讨

文 孙加振 魏先福 黄蓓青

丝网印刷技术作为四大印刷方式之一，以其可控的油墨墨层实现图像原稿再现，墨层厚度范围可从1μm到300μm，且承印尺寸范围可在几微米到几平方米之间，承印物范围广泛，甚至承印材料呈液体或悬浮于液体中。以往大量的研究都很好地讲述了平版印刷、凹版印刷、凸版印刷的表面科学问题，但很少有关于丝网印刷的表面科学问题分析。行业内普遍认为根据丝网印刷工艺的特征对表面科学问题进行分析很大程度上已经是一件可有可无的事情，但是，随着印刷技术发展以及与科学研究结合的需要，在丝网印刷工艺过程中探究相关的表面科学问题也就逐渐显现出了其关键性。本文将根据丝网印刷工艺自身的特点，从表面科学问题的角度展开对丝网印刷工艺的一个初步讨论，从而方便行业内相关人员更好的了解和使用丝网印刷并认识表面科学问题在丝网印刷应用中的关键作用，为丝网印刷的绿色化、功能化道路提供有意义的参考资料。

丝网印刷发展

丝网印刷最早起源于中国，距现在已有2000多年的历史了。早在我国秦汉时期就出现了夹颉印花方法，长沙马王堆出土的画卷，就是西汉时期的网印品，东汉时期的夹颉腊染产品开始流行。国外许多研究网印的学者不得不承认，丝网印刷是中国的一项发明。可惜的是，长期的中国封建社会桎梏了生产力，限制了丝网印刷技术的发展，特别是在以利用感光胶制网版为标志的现代丝网印刷中，中国落后了。在欧洲，到了18世纪左右，模版——漏空版已大量地用于墙壁纸的生产。1905年英国的萨姆埃鲁·希文研究出了使用丝绸网的印刷方法，并取得了专利。这种方法，传到美国后，一个叫琼·布鲁斯瓦斯的人对此又作了改进，研究出了用一张丝网进行多色印刷的方法，用于印制招牌。此后，网印技术便获得了飞速发展，在商业印刷中也被大量使用。近代以来，网版印用领域也不断扩大，在纺织、陶瓷、容器、标牌、广告及厚膜超集成线路和薄膜超导材料等的印刷方面都有应用。

丝网印刷原理

丝网印刷是将丝织物、合成纤维或金属丝网绷在木质或金属网框上，采用手工描绘雕刻或利用感光材料通过光化学的方法制成丝网印版。丝网印版的图像部分网孔能够透过油墨，在印刷过程中，通过刮板的挤压作用，油墨漏印至承印物上形成图文部分；印版上其余部分的网孔在制版过程中被堵死，不能透过油墨，在承印物上形成空白部分，完成油墨的转移。

图1 丝网印刷原理图

丝网印刷印版

了解了网版印刷的基本原理，就不难明白网印的制版原理。简单来说就是在丝网上形成能透过油墨的图文部分和不能够透过油墨的空白部分，印刷时，油墨在刮板的作用下，漏印至承印物上形成墨迹。

普遍使用的是感光制版法，首先是在绷好的丝网上涂布感光胶，形成感光版膜，然后利用感光材料的光硬化性，将阳图底版密合在版膜上晒版，经紫外线曝光、显影、冲洗得到丝网印版。由于印版上的图文部分不受光照射，感光胶膜可溶于水，冲洗后印版上只有丝网，形成通透的部分，印刷时能透过油墨，在承印物上形成墨迹，得到图文。印版上受光的部分感光胶硬化，不能溶于水，形成固化版膜，将网孔封住，印刷时油墨不能透过，就形成了空白部分。

图3 丝网印刷印版

丝网印刷油墨

丝网印刷要注意控制油墨流动性，流动性大印迹容易扩大；流动性小，印迹易结网（网点交织的结点），出现结墨现象（亦称网纹），一般以30mm～50mm为宜。流动性即流平性，是油墨在外力作用下向四周展开的程度，与油墨的塑性和触变性都有关系，塑性和触变性大，流动性就小；反之流动性则大。触变性是油墨溶胶和凝胶的互换现象，油墨静止一定时间后变稠，粘度变大，搅动后变稀，粘度又变小，有利于保证其保真性。可塑性是指油墨受外力作用发生变形后，仍保持其变形前的性质。油墨的可塑性有利于提高印刷精度。另外，粘度直接影响着油墨转移性和印品质量，水性油墨粘度过低会造成色浅、网点扩大、传墨不均匀等弊病；粘度过高，油墨转移性能较差，易出现脏版、糊版等现象。在印刷过程中对油墨粘度的控制是非常重要的，实际制备中油墨流变性与连接料、颜料用量、分散状态及印刷温湿度等有关。

表面科学问题

在丝网印刷中，不难看出包括油墨铺展到印版、油墨通过印版网孔、油墨转印到承印物上。实际上，任何一个固体表面都不可能是绝对光滑、均匀的，实际的表面都是有一定的粗糙度，因此必须考虑粗糙度对表面浸润性的影响。目前，最普遍应用于解释液滴表观接触角与固体表面粗糙度之间联系的是Wenzel和Cassie方程。下面从这个方面展开液体与固体之间的关系，从而可以对丝网印刷中油墨与印版之间的表面科学关系中的科学问题进行探讨。

Wenzel方程：早在1936年Wenzel就认识到了粗糙度对固体表面浸润性的影响，他认为在Wenzel浸润状态时，液体和粗糙固体表面接触的部分是完全浸润的。考虑到粗糙度对表面浸润性的影响，他将Young's方程修改为：

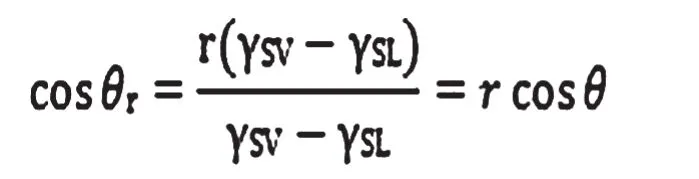
式中 r 定义为粗糙度，是指实际的固/液界面接触面积与表观固/液界面接触面积之比(r≥1)，θr是粗糙表面的接触角。

Wenzel方程表明，粗糙表面的存在使得实际上固/液的接触面要大于表观几何上观察到的面积，于是在几何上增强了疏水性 (或亲水性)。即：(a)θ<90°时，θr随着表面粗糙度的增加而减小，表面变得更亲水；(b)θ>90°时，θr随着表面粗糙度的增加而变大，表面变得更疏水。

应该指出的是，Wenzel方程只适用于热力学稳定平衡状态，但由于表面不均匀，液体在表面上展开时需要克服一系列由于起伏不平而造成的势垒。当液滴振动能小于这种势垒时，液滴不能达到Wenzel方程所要求的热力学平衡状态而可能处于某种亚稳平衡状态。

Cassie-Baxter方程：Wenzel方程揭示了均相粗糙表面的表观接触角与本征接触角之间的关系。当固体表面由不同种类的化学物质组成时，则不适用于此方程。Cassie和Baxter进一步拓展了Wenzel的上述处理，提出可以将粗糙不均匀的固体表面设想为一个复合表面，即他们认为液滴在粗糙表面上的接触是一种复合接触。当固体表面的粗糙不均匀性表现为宏观起伏到一定程度时，空气就容易被水截留在固体表面的凹谷部位。在这种情况下，复合表面的表观面积的成分也可用它们各占单位表观面积的分数f1和f2(f1+f2=1)来表示，它们相应的本征接触角用θ1和θ2来表示。一般地，描述复合表面的公式为：

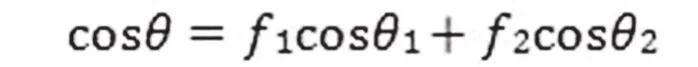
此即 Cassie-Baxter方程。该方程也适用于具有多孔的物质或粗糙至能截留空气的表面。此时f2为多孔的分数或截留空气部分的表观面积分数，由于空气对水的接触角θ2=180°。因此，上式可以变为：

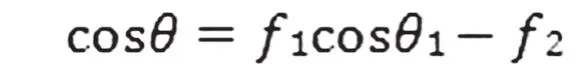
上式中f1和f2分别表示固/水界面和水/气界面所占的分数(f1+f2=1)。但是，在上面方程中，对任意粗糙的表面来说，要准确确定f1和f2的值是很困难的。实际上，常见的f1部分所表示的界面并非光滑平坦的表面，所以还需在上述的公式中引入粗糙度系数r来修正，则：

对于不同粗糙结构的表面，粗糙系数r将取不同的数值。同时，从上述方程还可以看出，当本征角大于90°时，表面粗糙度的增大将增大表观接触角的大小。这一点与Wenzel方程不同，因为即使是本征接触角小于90°的平滑表面，也可以由于超疏水性的存在使得接触角增加。

固体表面Wenzel和Cassie浸润状态之间的关系与转变：

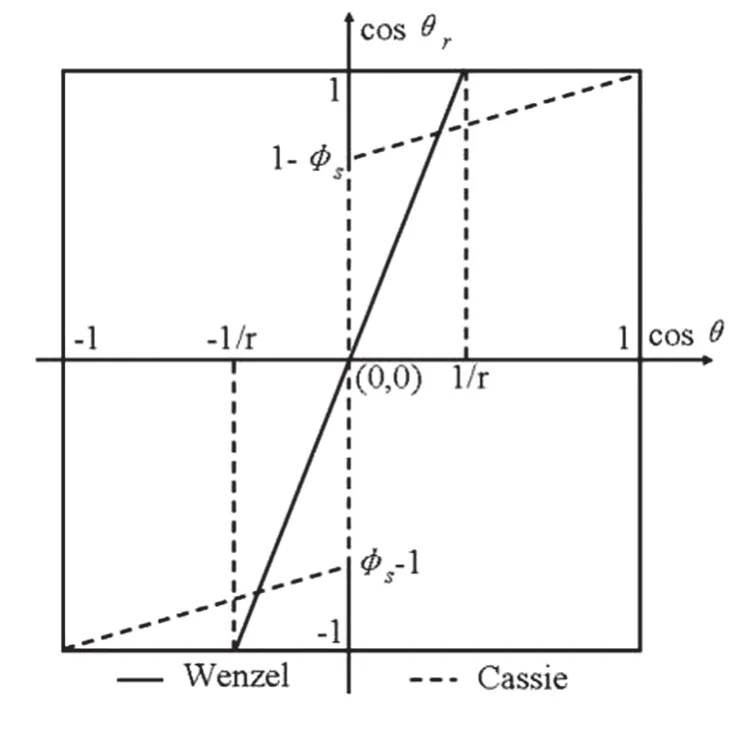
图4 粗糙表面本征接触角θ与表观接触角θr之间的余弦关系

对于不同粗糙度的表面，其本征接触角θ与表观接触角θr之间的关系可以用上图来表示，图中同时给出了适用于Wenzel状态与Cassie状态的θ与θr之间的线性关系，这一关系与Shibuichi得出的实验结果与上图所示相一致。Dettre和Johnson在总结Wenzel及Cassie方程的基础上，通过模拟粗糙表面发现，表面的粗糙度因子存在一个临界值，超出这一临界值，固体的表面浸润性会从适用于Wenzel方程变化到适用于Cassie方程。表面粗糙度越大，Cassie状态和Wenzel状态之间的能垒越高，Cassie状态越稳定。

图5 粗糙表面本征接触角θ与表观接触角θr之间关系的实验结果

然而，对于具有同一粗糙度的表面，也可能有两种浸润状态，即有Wenzel和Cassie两个状态的表观接触角，这样就涉及到两种浸润状态之间的转变问题。

当一个液滴在固体表面处于Cassie状态，其接触角符合Cassie方程时，在外界刺激如应力、光、电、热、磁等的作用下，其形貌将发生变化，液体将填满粗糙固体表面的沟槽，同时导致固体表面失去疏水性，进而其表观接触角也将由符合Cassie方程转变成符合Wenzel方程。

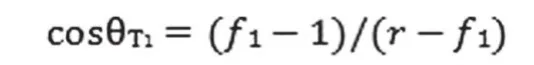
当浸润性从Wenzel态向Cassie态转变时，其接触角是增加的，并且其接触角符合上文方程。通过联合以上两个方程可以得到临界转变角度θT1。

如果Young's接触角θ<θT1，那么液体和固体接触部分所包含的空气是不稳定的，浸润性很容易从Cassie态转变成Wenzel态。为了得到比较稳定的束缚空气层，固体表面必须足够的疏水，临界转变角度必须足够小，因为Cassie浸润状态只有在θ>θT1或cosθ<-1/r时是稳定的。但是上述公式还只是经验性和模型化的结果，因为固体表面不一定符合公式所描述的情况，它与表面的形貌有关。

因此，本文通过对丝网印刷的介绍及现在广泛使用表面科学探讨方法，将丝网印刷与表面科学进行了联系。后可以对丝网印刷中的表面科学问题进行分析，结合表面科学问题的探讨，联系丝网印刷中的表面性能要求，建立油墨、印版、外力之间的关系。从而，得出丝网印刷中油墨、印版在表面科学方面的关系式，了解、指导、完善丝网印刷。