人工判读误差对人动作技术量化分析影响的实例研究

王晓刚，张 颖

(中北大学体育学院，山西 太原 030051)

在利用影像测量手段对动作技术进行分析时，对关节点坐标的获取常常需要人工操作来实现。因而，测量数据的可靠性以及人工判读过程中所产生的误差，将会对最后的研究结果产生直接的影响。有研究表明，当测试者间差异大于运动本身差异时，测试得到的数据可靠性会大大降低［1］。另外一些研究则针对运动分析系统的有效性和可靠性进行了验证［2－3］，但这些研究主要针对的是自动反光捕捉系统的测试，而在一些室外测试过程中，自动捕捉系统会受到光线等因素的影响而失效。因此，本研究的目的是通过对室外拍摄获取的动作图像进行人工解析，并对此过程中由人工解析产生的误差对解析结果的影响进行研究。

1 研究对象与方法

对4名跨栏运动员分别进行的8次试跑动作进行拍摄，每次试跑过程跨越4个栏架。利用两台常速摄像机对第3个栏架的跨越动作进行拍摄，拍摄频率为50Hz，快门速度为1/1000s。两台摄像机距离栏架25m，主光轴对准栏架中心。其中一台位于栏架正前方，另一台位于栏架正侧方，两台主光轴夹角为90°。栏间距分别为8.2m(女子)和8.8m(男子)，栏高均为标准高度。

两台摄像机的拍摄范围分别为6.7m(女子)和7.3m(男子)。在测试前，将爱捷三维标定框架(25个控制点)放置于距离栏架前0.5m处，并进行拍摄。

在32次试跑中随机选取了两次(一名女子和一名男子)进行解析，解析工作由同一名解析员重复进行8次，解析使用APAS运动图像解析软件。解析动作过程从支撑腿着地瞬间开始到攻栏腿着地瞬间结束，女运动员为35幅图像，男运动员为33幅。在解析时，使用丹普斯特人体惯性参数模型，解析点数量为19个，计算机屏幕分辨率为640×480。

两台摄像机(1T文件和2T文件)所解析得到的二维原始坐标参数(u，v)以及经直接线性变化得到的3D坐标(3D文件)参数均导入Excel软件中，并分别计算出每幅图像中8次解析得到的19个人体标志点的标准差值(SD)。将每一个方向上，各标志点的最小标准差值(SDmin)作为基本单位，其他时刻的SD均以此基本单位做标准化处理。另外，3D方向坐标值通过矢量合成的方法计算得到。

2 结果与分析

2.1 重复解析最小标准差值情况分析

在本研究中，由于无法得到人体标志点坐标真值，因此，无法对两台摄像机单独获得的坐标值与三维重构后的坐标值直接进行比较。在这里，选择SDmin(单幅画面中所有标志点重复解析的最小标准差值)作为基本单位，是因为其代表了解析员对此标志点的最佳判读精度。

研究的结果表明(表1)，各身体标志点的SD值都在某幅画面(某个方向)中作为所有标志点坐标值的SDmin值出现过。其中，出现SDmin次数最多的为肩线中点(20次)，最少的为右髋(3次)。即便是通常被认为精度较差的髋关节点，虽然SDmin出现的次数为左髋4次和右髋3次，但说明这些标志点只要同时被两台摄像机清楚的捕捉到，同样可以获得精度较高的解析值。而起跨腿膝关节以及同侧手臂的某些关节点的SD值在整个攻栏过程中都大于其他标志点。这些点由于躯干以及身体其他部位的遮挡，增大了解析结果的不可靠性。

表1 身体各标志点坐标值的SDmin出现频次统计情况

表2是对各身体标志点进行重复解析后的SD值统计情况，反映了在不同方向解析精度的变化范围。其中，最大SDmin值表明各身体标志点在x、y、z方向上的最佳解析精度都可以达到0.01m以下。因此，当身体标志点清晰可见时，解析结果的可靠性还是很高的。从标准差均值范围可见，大部分身体标志点的解析精度是可靠的。另外，从表2和表3的数据结果我们还可以看出，垂直方向的解析精度略高于其它方向。

表2 女子身体标志点重复解析精度情况统计

表3 男子身体标志点重复解析精度情况统计

2.2 对两摄像机平面解析精度的分析

在对所有标志点坐标进行标准化处理后发现，两台摄像机(1T和2T)解析得到的标准差值变化范围较大，男女运动员的 SD/SDmin值分别为1－30和1－22.5。虽然较大的SD/SDmin值出现的次数较少，且都不是出现在关键时相，例如过栏等画幅中，但是这必须引起我们足够的重视。如果在某些关键时相中，SD/SDmin值过大，就有可能对动作技术分析的结果产生影响。

在对男运动员的研究中，由于在过栏过程中，位于栏架正侧面摄像机拍摄的画面中，起跨腿和同侧的手臂被躯干所遮挡，因此在解析时增加了判读的难度。从解析结果来看，虽然没有对运动员身体重心最高点的坐标值产生太大的影响(SD=0.01m)，但对“重心距栏架中心距离”这一参数影响较大(SD=0.11m)。女运动员由于起跨腿轨迹较低，遮挡情况不明显，因此对上述参数的影响不大(SD=0.00m和0.01m)。

从整体来看，绝大多数画幅中的身体标志点的SD/SDmin值都小于4，这说明由同一解析员解析得到的数据可靠性较高。在对两台摄像机进行平面解析的结果中(1T和2T文件)，所有解析得到的身体标志点的u、v方向坐标的平均SD值与SDmin的比值在2.6－7.1(男运动员)和2.3－8.7(女运动员)之间。在对坐标值进行重构后，女运动员单个身体标志点在x、y、z方向以及合方向上的最大 SD值分别为0.017m、0.009m、0.016m和 0.025m;男运动员为 0.017m、0.012m、0.018m 和0.027m。

2.3 平面解析精度对三维重构精度的影响

我国学者杨年峰［4］等人研究了各坐标误差对三维重构坐标的影响，结果表明三维重构的各分坐标对象坐标误差具有不同的敏感度。图1－图3是对女运动员右肘关节点坐标值的解析情况，包括每台摄像机的二维坐标以及三维重构后的误差情况，在一定程度上反映了三维影像解析过程中平面解析误差对三维重构精度的影响。从图中可以看出，在过栏过程中，侧面摄像机位置(1T)由于肘关节被躯干所遮挡，因此，在重复解析时得到的右肘关节点坐标值表现出很大的不稳定性。在所解析的35幅画面中，u、v以及合方向上SD/SDmin＜4的画幅数分别为15幅、13幅和18幅。而另一台摄像机(2T)由于整个拍摄过程中，运动员右肘关节点始终没有被遮挡，因此三个方向上SD/SDmin＜4的画幅数分别为27幅、26幅和28幅。

图1 1T文件解析后的u、v坐标精度曲线图

图2 2T文件解析后的u、v坐标精度曲线图

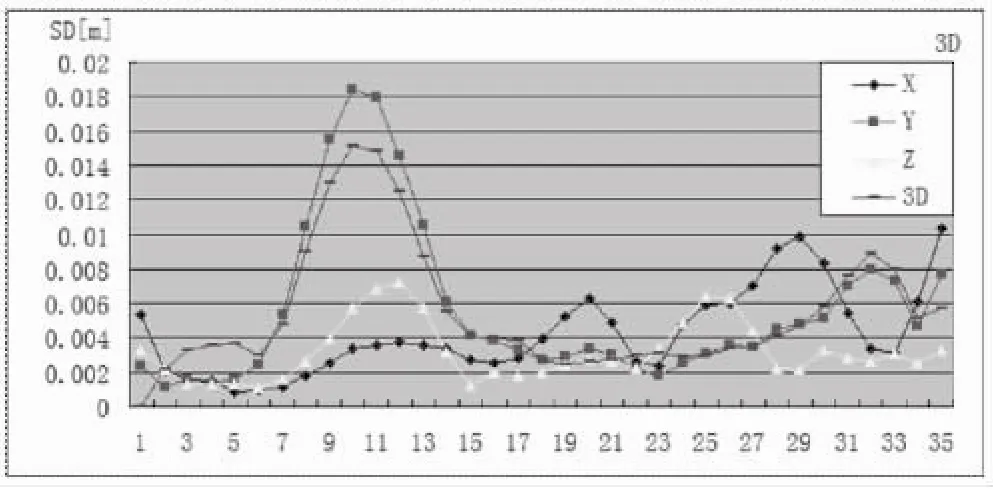
图3 三维重构后得到的各方向上坐标精度曲线图

在本研究中，进行三维重构后，所有画幅中三维坐标各方向(x、y、z以及合方向)的SD值变化范围为在0.0022m(y轴)至0.047m(合方向)之间。在解析得到的所有画幅中，三维重构后，男运动员单个身体标志点最大SD值为0.085m(起跨腿膝关节点)，女运动员为0.056m(右手点)。从图1－图3我们可以看出，任何一个画面中解析精度的改变对三维重构后的精度都会产生较大的影响。

2.4 速度及角速度参数解析精度的分析

我们对跨栏项目动作技术分析中常用的28个参数指标进行了分类，分为9个位移参数，5个线速度参数，8个角位移量，3个角速度参数和3个其它变量。在位移参数中，除男运动员“重心最高点距栏架中心距离”这一参数的 SD值大于0.01m(SD=0.11m)之外，其余都小于或等于0.01m。角位移参数中，SD值在0°－2°之间(除男子起跨腿膝关节角度 SD=3°)。速度参数的SD值在0.1－0.2m/s之间。角速度参数SD的最大值，男运动员为140°/s(平均值为1046°/s)，女运动员为 113°/s(平均值为 777°/s)，这样的解析精度决定了角速度参数只能用来对某些动作进行定性分析，而不能进行量化研究。

2.5 数据平滑对研究结果的影响

数据平滑技术是消除随机误差对研究结果造成影响的主要方法。在本研究中，采用的平滑方法为数字滤波法，截断频率为8Hz。通过平滑前后对比后发现，虽然对大部分位移量参数的影响并不大，但对某些关键参数的影响也是不容忽视的。例如，在对“重心最高点距栏架中心距离”的对比研究时，由于女运动员身体重心轨迹比较平稳，因此平滑前后参数变化不是十分明显，分别为 0.36 ±0.01m 和 0.25 ±0.07m。但对于男运动员来说，这一参数在平滑前后的变化就较为明显，分别为 －0.12 ±0.11m 和 －0.01 ±0.01m。

3 结论

(1)利用重复解析的方法证明，在研究跨栏运动时，大部分运动学参数的解析精度能够满足研究的要求。

(2)在利用影像测量方法对动作技术进行比较分析时，对个别运动学参数的使用，例如“重心最高点距栏架中心距离”等要慎重。

(3)在进行三维重构时，任何一个平面的解析精度都会对三维重构的精度带来影响。即使是解析难度较大的身体标志点，只要在两台摄像机中都能够清晰成像，同样可以获得较高的解析精度。

［1］Roger Bartlett_，Melanie Bussey，Nick Flyger.Movement variability cannot be determined reliably from no－marker conditions［J］.Journal of Biomechanics，2006(39):3076 －3079.

［2］Paul Glazier，Movement Variability in the Golf Swing:Theoretical，Methodological，and Practical Issues［J］.Research Quarterly for Exercise and Sport，2011(82):157 －161.

［3］Yeadon，M.R.＆ Challis，J.H..The future of perlormancerelated sports biomechanics research.［J］.Journal of Sports Sciences，1994(12):3 －32.

［4］杨年峰，等.DLT算法中象平面误差对三维重构的影响［J］.中国生物医学工程学报，2000(19):121－130.