随机需求航线网络效应下机队鲁棒优化方法

汪 瑜，朱金福，葛 伟

(1.中国民航飞行学院航空运输管理学院，四川 广汉 618307;2.南京航空航天大学民航学院，江苏 南京 210016)

明确航空公司拟运营区域未来一段时期内机队的规模与结构，是确保航空运输企业在需求旺季时实现运营利润最大化的前提，也是航空公司在需求淡季时降低运营过剩运力的保证.鲁棒的机队构成可以提高民航企业优化稀缺资源配置的能力，因此，合理有效的机队鲁棒优化方法关系到民航运输企业的运营成本和风险可控性，是获取最大收益的关键性战略决策.

文献［1］在分析机队规划基本方程的基础上，给出了宏观规划的经验分析方法.文献［2］在航空公司未来拟运营网络环境的层面上建立了机队宏观规划的数学模型.文献［3-7］从航班/航线机型分配的角度构建了微观机队规划数学模型，并探讨了机队的鲁棒性规划方法.文献［8］利用数学模型分析了机队构成与航线特征的关系，指出了航空管制因素对航空公司机队构成的影响.文献［9］利用成本分析法分析了欧盟碳排放规则对于机队构成的影响.文献［10-11］在考虑了需求限制、机场交通流限制等因素的基础上，构建了微观机队规划数学模型.

通过上述分析可以发现，基于航线网络层面的宏观机队规划法［1］虽然简单易操作，但却很难反映出旅客需求溢出对于拟运营机队构成的影响，也无法准确反映机型航线的适应性问题.而从航线/航班层面的微观机队规划法［3］又很难准确反映出未来机队拟运营环境的特点，例如旅客需求的不确定性、生产运营组织模式特征等.加之国内各大航空公司生产运营模式向枢纽轮辐式航线网络结构的转型，大量的中转衔接旅客在增加航段旅客流量的同时，又使得流经航段的旅客组合更为复杂，这些现象导致传统微观机队规划法已经无法准确评估航段旅客组合［12-13］对于机队构成的影响.因此，从旅客组合优化角度研究机队的鲁棒优化方法，对于航空公司准确把握未来拟运营环境中所需机队的规模与结构有重大的现实意义.

本文首先通过比较全连通航线网络与枢纽轮辐式航线网络两种不同航班运营组织模式对于机队构成的影响，指出在具有旅客中转衔接的航班组织模式(例如枢纽轮辐式航线网络运营模式)下旅客需求溢出的网络效应问题，同时又进一步说明从航线网络环境运力优化配置角度构建机队规划方法的必要性;其次，以机队规划成本最小化为目标函数，综合考虑未来拟运营区域内航班频次限制、旅客需求限制、飞行时间限制等资源约束，构建航空公司机队的鲁棒优化模型;然后，通过构造旅客需求的离散情景集，利用情景汇聚(scenario aggregation)算法求解机队规划问题;最后，通过算例验证了机队规划方法的有效性.

1 问题提出

从微观层面构建机队规划方法必须准确模拟企业在未来一段时期内的运营环境，然而在枢纽航线网络运营模式下，某一航段旅客的溢出很有可能会造成整个航线网络环境内旅客流量的下降，进而导致传统基于航段的微观机队规划法无法准确评估旅客溢出成本对于机队规划结果的影响.图1(圈内字母表示机场，线上数字表示座级)给出了全连通航线网络结构与枢纽轮辐式航线网络结构下，不同航班运营模式对机队构成的影响.全连通航线网络是指任意两个城市之间都有直达航班的航线网络;枢纽轮辐式航线网络是指航线的安排以某个城市为枢纽，其它城市之间没有直达航线，而是都与枢纽相连，通过枢纽进行中转衔接［14］.

假设在充分考虑航班机型运营成本的前提下，图1(a)的全连通航线网络结构中可以采用110座级的飞机运输8次，而在图1(b)的枢纽轮辐式航线网络结构中，H点成为枢纽且为其它节点旅客需进行转运，此时需要采用260座级的飞机运输4次，但同时会导致10位旅客需求溢出，若溢出的是中转衔接旅客，就会造成其它衔接航段上旅客同时溢出的现象(即航线网络效应)，因此，在机队规划时准确反映该效应是提高机队规划准确性的关键.

与全连通航线网络结构不同的是，由于枢纽航线网络结构采用航班中转衔接模式运输旅客，这使得流经任一航段的旅客会产生叠加现象.叠加现象可以保证航空公司采用更大座级飞机执飞而形成一定的网络经济性，因此，准确反映航线网络构型对于需求的影响同样也是保证机队规划结果准确性的关键.

图1 不同航线网络运营模式对机队构成的影响Fig.1 Impact of different route network operation modes on fleet composition

2 模型建立

考虑旅客需求溢出的网络效应，机队规划过程必须考虑旅客的组合优化问题.航段上旅客需求的叠加现象，又使得机队规划过程必须考虑航线网络运力的优化分配问题.鉴于此，本文在充分考虑旅客组合优化问题的基础上，利用需求运力优化配置技术构建航空公司的机队规划数学模型.

2.1 符号说明

基于航线网络效应下的运力优化配置的机队规划模型决策变量与参数说明如下:

zk为决策变量，表示在机队规划期内所需机型k(k∈K)飞机的架数，单位:架;

xik为决策变量，表示机型k飞机执飞航段i(i∈I)的频次，单位:次;

ypr为决策变量，表示同一市场上行程路线p(p∈P)溢出至行程路线r(r∈P)上的旅客数，单位:人次;

ak为在机队规划期内机型k(k∈K)飞机的平均单位采购成本，单位:万元;

bpr为行程路线p(p∈P)上的旅客溢出至行程路线r(r∈P)上的再捕获率;

δpi为 0-1 变量，

cik为机型k飞机执飞航段i发生的变动成本，单位:万元/次;

fp为行程路线p上旅客的平均票价，单位:万元;

Fi为航段i上航班的最大飞行次数，单位:次;

Ccapik为机型k飞机执飞航段i的实际可用座位数，单位:个;lik为机型k飞机执飞航段i的期望客座率;dp为行程路线p上的旅客数，为需求随机变量，单位:人次;

tik为机型k飞机执飞航段i的轮挡飞行时间，单位:h;

mk为机型k飞机的日期望利用率，单位:h.

2.2 数学模型

航空运输市场的季节性特征使得旅客需求具有不确定性，该现象使得传统确定性机队规划法所得出的机队构成无法很好地适应市场需求的波动.例如，在需求旺季时，会由于公司运力不足而导致收益的大量流失;而在需求淡季时，又往往会由于运力过剩而导致不必要的成本支出.因此，本文将旅客行程路线上的旅客需求视为随机变量，并构建机队的鲁棒优化模型.判断机队构成优劣需要一个统一的评估指标，本文构建的机队规划成本包括:

(1)机队采购成本;

(2)机型航段运行变动成本;

(3)旅客需求溢出成本.

构建的机队鲁棒优化模型可以描述为

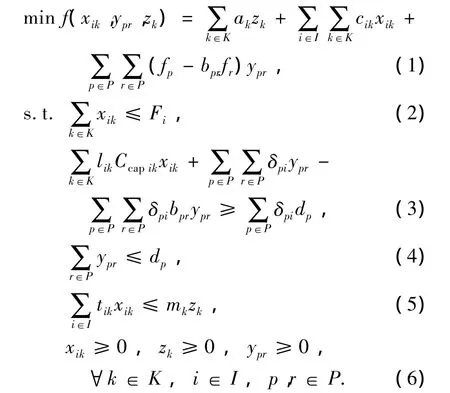
式(1)表示机队规划成本最小化目标函数;式(2)表示任一航段i上执飞的航班频次不能超过其所允许的最大航班数量;式(3)和(4)是旅客组合优化模型约束，式(3)表示任一航段i上承载的旅客人数不小于实际经过该航段的旅客人数，式(4)表示任一旅客行程路线p上的溢出人数不能超过该行程路线的需求量;式(5)表示第k种机型机队的实际轮挡飞行小时数不超过机队所能提供的最大轮挡飞行小时数;式(6)为决策变量的类型与取值范围.

需要说明的是，在行程路线p与r相同时，旅客溢出的再捕获率是相同的，即 bpp=1，此时，式(1)中第3项的系数(fp－bppfp)为0.

由于式(1)以机队规划成本最小化为目标函数，因此，决策变量ypp反映了实际承载行程路线p上的旅客数量.另外，针对旅客实际溢出问题，本文设计了虚拟旅客行程路线，用yp表示从行程路线p溢出后转至虚拟旅客行程路线的旅客数.

3 算法设计

旅客需求的不确定性使得鲁棒优化模型中旅客需求的转移和再捕获过程变得复杂化，因此，本文采用情景汇聚算法［7，15-17］进行求解.情景汇聚算法的基本思想可以描述为:首先，假设旅客需求服从正态分布，按照等间距划分需求累积概率值的原则，将每个行程路线上的旅客需求概率分布范围进行划分并产生需求情景(scenario)集S;然后，构造机队规划目标函数的增广拉格朗日函数，且对第s(s∈S)种情景求解其增广拉格朗日函数值，并将机队构成决策变量值进行汇聚;最后得出期望机队规划成本最小的鲁棒机队构成.算法步骤如下:

(1)产生需求情景集.根据行程路线p上的旅客需求分布函数，按照等间距划分需求累积概率值的原则，利用式(7)进行等分并产生个需求，对这些需求进行随机排列后形成行程路线层面上的需求情景集

式中:N为行程路线数目.

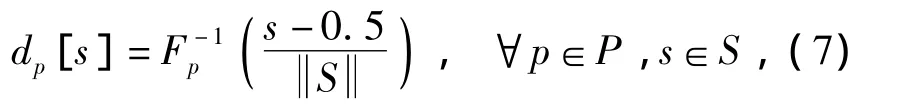
式中:F为需求累积分布函数.

(2)构造增广拉格朗日函数.设¯zk表示待求解鲁棒机队构成决策变量，为了保证机队构成在任意情景下的一致性，在机队规划模型(式(1)～(6))的基础上，还必须满足约束条件式(8).因此，构造第s种情景下的增广拉格朗日函数如式(9)所示.

式中:f(xik(s)，ypr(s)，zk(s))为情景s下机队规划成本的目标函数;

wk为拉格朗日乘子.

(3)计算需求再捕获率.利用工业指标量化市场份额指数(quantitative share index)［12］，计算情景s下旅客从行程路线p转移至r(r∈P)的需求再捕获率，如式(10)所示.

式中:qr(s)为情景s下行程路线r对旅客的吸引力.

(5)迭代求解情景汇聚模型.对于每一情景，求解以式(9)为目标函数、式(1)～(6)和(8)为约束条件的数学规划模型.判断规划结果是否满足式(11)的终止条件，若是则停止，并按式(12)计算随机情景下期望的机队规划成本G，并将其作为情景汇聚算法求解的目标函数值;否则，按式(13)和(14)分别更新拉格朗日乘子w(t)k和变量 ¯z(t)k的值，重复步骤(5)，直至满足式(11)为止.

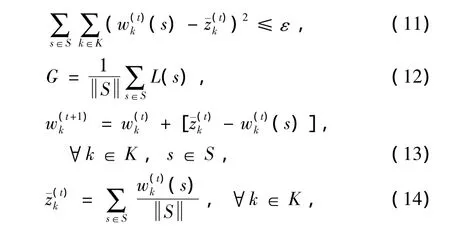
式中:ε为预先设定的一个充分小的非负实数.

考虑到旅客需求为符合正态分布的连续型随机变量，因此，在求解步骤(5)中的数学规划模型时，可以将变量ypr松弛为非负实数.

4 算例

为了说明本文设计方法的有效性，采集图2所示航线网络结构运营模式的某航空公司运营数据(见表1和表2)，利用ILOG/CPLEX软件对6种候选机型、12个航段、57条旅客行程路线进行分析.根据算法的收敛性以及决策变量的类型，本文给定情景汇聚算法的收敛条件为ε=10－6.

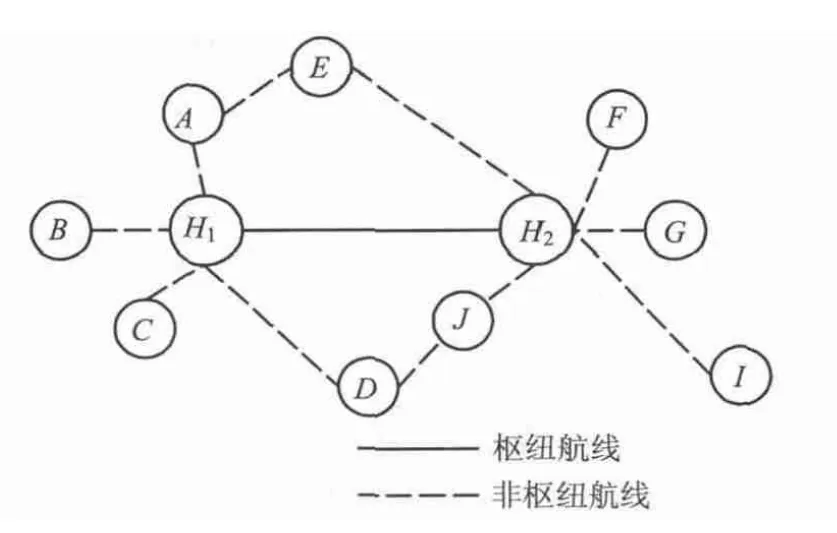
图2 非严格枢纽轮辐式航线网络结构运营模式Fig.2 Operation mode of nonstrict hub-and-spoke airline network structure

表1 航线网络环境下机型运营信息Tab.1 Operation information of fleet types under airline network environment

表2 航线网络环境下航段运营数据Tab.2 Leg-based operation data under airline network environment

图2中所有轮辐机场的旅客只能通过枢纽机场H1和H2进行中转，且轮辐机场之间没有旅客中转衔接功能.

从表3可见，与不考虑旅客网络效应问题的基于航段的机队规划方法(传统机队规划模型)相比较，本文所设计的机队规划模型的机队构成为:机型2/1架，机型 3/76架;机型 4/1架，机型 6/12架.机队规划成本相应减少了167.07万元，而溢出人数、溢出率(指溢出人数与旅客需求总数的比值)以及溢出成本(指溢出人数与平均票价的乘积)却分别增加了 1606.66人次、8.27% 和222.46 万元.

另外，两种方法所得出的飞机数目相差7架，这意味着传统机队规划法中旅客溢出成本的减少是以增加飞机运行频次(飞机数)为代价的，而飞机数的增加意味着更多采购成本的支出，因此，合理的旅客需求溢出对于航空公司机队规划决策在一定程度上是有利的.该现象也充分说明了枢纽航线网络运作模式下本文所设计机队规划方法的优势.

为了说明情景汇聚算法的有效性，将本文设计算法求解得出的期望解与确定解的随机期望值进行比较.通过表4可以发现，在情景数目为20、40和60个时，随机规划期望解的各项指标(机队构成、机队规划成本、旅客溢出数、旅客溢出率和旅客溢出成本)的偏差保持了一定的稳定性，这说明情景数目的取值对于情景汇聚算法求解结果稳定性的影响较小.另外，对比随机规划的期望解与确定解的随机期望值，可以发现在情景数目为20、40和60个时，利用情景汇聚算法所得出的机队规划成本分别减少了19.88、21.02 与 17.55 万元，这表明了在需求不确定性前提下，本文所设计算法的有效性.3种情景下的旅客溢出数、溢出率以及溢出成本的变化也充分说明了机队在需求不确定性前提下，虽然提供更多运力会引起额外的固定成本支出，但可以有效的避免旅客溢出所带来的成本损失，而当这种旅客溢出损失大于机队固定成本增加时，那么就应该选择更多运力的机队决策方案.

综上所述，本文在考虑需求不确定性前提下所设计的算法能够有效地降低机队规划成本，因此，所得出的机队构成能够更好的适应市场需求的波动，具有更好的鲁棒特点.

需要说明的是，随机规划模型的期望解是指相应决策变量与目标函数的解，以及在此基础上所形成的相关指标的解;确定解的随机期望值是指以旅客需求均值为基础求解得出的机队规划的确定解，并以此为基础进一步求解得出的各种情景下最小机队规划成本的相关解的期望值.

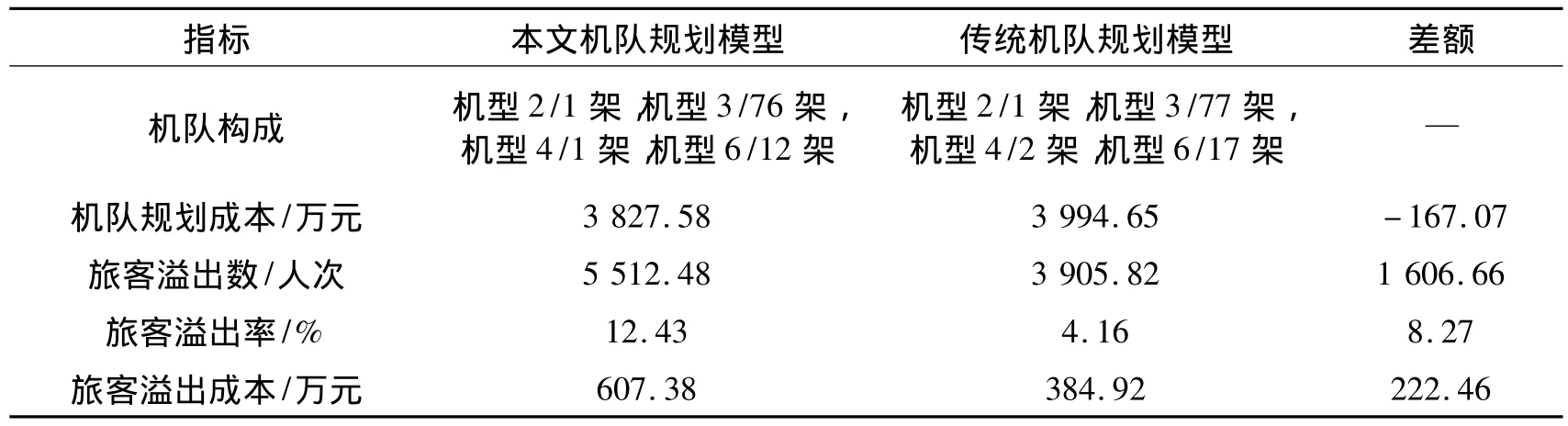
表3 与传统机队规划模型计算结果的相关指标比较Tab.3 Comparison to the results from traditional fleet planning model on related indices

表4 随机规划的期望解与确定解的随机期望值的比较Tab.4 Comparison between the expected solution to stochastic planning and the deterministic solution to stochastic expectation

5 结束语

本文利用需求运力优化配置技术，结合各航段机型最大飞行频次限制、最大旅客需求限制以及机队最大飞行时间限制等因素，将旅客组合优化方法应用到机队规划问题之中，在考虑旅客溢出再捕获情况的基础上，构建了基于航线网络效应下运力优化配置的机队鲁棒优化模型，并在旅客需求不确定性的基础上，利用情景汇聚算法求解机队的鲁棒性优化数学模型.案例分析表明，基于航线网络效应的机队规划方法能够有效降低机队规划成本;利用情景汇聚算法求解得出的机队随机规划期望成本值比确定解下的机队规划成本最小期望值更低.因此，本文设计的机队规划方法所得出的机队构成能够更好的适应市场需求的波动，且是有效可行的.考虑航空公司备份运力以及因维修计划所需周转运力的需要，公司实际运营所需的飞机数应多于本文计算结果.

［1］彭语冰，张永莉，张晓全.机队规划模型的建立及其应用［J］.系统工程:理论与实践，2001，21(6):100-103.PENG Yubing，ZHANG Yongli，ZHANG Xiaoquan.Fleetplanning modeling and its applications［J］.Systems Engineering:Theoryand Practice， 2001，21(6):100-103.

［2］朱金福.航空运输规划［M］.西安:西北工业大学出版社，2008:238-240.

［3］汪瑜，孙宏.基于航班机型分配技术的机队规划启发式算法［J］.系统工程:理论与实践，2011，31(2):371-378.WANG Yu，SUN Hong.Heurist algorithm of fleet planning based on airline fleet assignment［J］.Systems Engineering:Theory and Practice，2011，31(2):371-378.

［4］汪瑜，孙宏.航空公司机队的鲁棒性规划启发式算法［J］.系统工程:理论与实践，2013，33(4):963-970.WANG Yu， SUN Hong. Heuristic algorithm to incorporating robustness into airline fleet planning［J］.Systems Engineering:Theory and Practice， 2013，33(4):963-970.

［5］孙宏，张培文，汪瑜.基于航线网络运力优化分配的机队规划方法［J］.西南交通大学学报，2010，45(1):111-115.SUNHong， ZHANG Peiwen， WANG Yu. Fleet planning approach based on route fleet assignment optimizing［J］. Journal of Southwest Jiaotong University，2010，45(1):111-115.

［6］段晓江，冯允成.启发式民用飞机机队规划［J］.北京航空航天大学学报，1996，22(4):504-508.DUAN Xiaojiang，FENG Yuncheng.Efficient heuristic algorithm to airline fleet planning［J］. Beijing University of Aeronautics and Astronautics， 1996，22(4):504-508.

［7］LISTES O，DEKKER R.A scenario aggregation-based approach for determining a robust airline fleet composition for dynamic capacity allocation［J］.Transportation Science，2005，39(3):367-382.

［8］BROWN J H. Airline fleet composition and deregulation［J］. Review of Industrial Organization，1992，8(4):435-449.

［9］TSAI W H，LEE K C，LIU J Y，et al.A mixed activity-based costing decision model for green airline fleet planning under the constraints of the European Union Emissions Trading Scheme［J］.Energy，2012，39(1):218-226.

［10］ZHURBENKO N G，PINAEY E G，SHOR N Z，et al.Choice of fleet composition and allocation of aircraft to civilairline routes［J］. Cybernetics and Systems Analysis，1976，12(4):636-640.

［11］都业富.机队规划的优化［J］.系统工程:理论与实践，1997，23(7):136-138.DU Yefu.Optimization of fleet planning［J］.Systems Engineering:Theory and Practice，1997，23(7):136-138.

［12］BARNHART C，KNIKER T S，MANOJ L.Itinerary-based airline fleet assignment［J］. Transportation Science，2002，36(2):199-217.

［13］JACOBS TL， SMITH BC， JOHNSON EL.Incorporating network flow effects into the airline fleet assignment process［J］.Transportation Science，2008，42(4):514-529.

［14］柏明国，朱金福.全连通航线网络和枢纽航线网络的比较研究［J］.系统工程:理论与实践，2006，26(9):113-117.BAI Mingguo，ZHU Jinfu.Comparative study on fully-connected and hub-and-spoke airline networks［J］.Systems Engineering:Theory and Practice，2006，26(9):113-117.

［15］ROCKAFELLAR R T，WETS R J B.Scenarios and policy aggregation in optimization under uncertainty［J］. Mathematics Operation Research，1991，16(1):119-147.

［16］CAROE C C，SCHULTZ R.Dual decomposition in stochastic integer programming［J］. Operation Research Letters，1999，24(2):37-45.

［17］WATSON J P，WOODRUFF D L.Progressive hedging innovations for a class of stochastic mixed-integer resource allocation problems［J］. Computer Management Science，2011，8:355-370.