城市路网模块结构探测及Hub路段诊断算法

胡郁葱，陈海伟

(华南理工大学土木与交通学院，广东 广州 510640)

近年来，复杂交通网络的研究引起了众多学者的广泛关注.一些实证研究表明，城市路网和其他网络一样，具有复杂网络的结构和功能特性，可以用复杂网络的思想对城市路网进行研究［1-4］.

模块结构是复杂网络的一个重要属性，主要表现在每个模块结构内的连接非常紧密，而模块结构之间的连接却相对比较松散.图1中网络包含3个模块结构，分别对应于虚线圆圈包围的部分.每个模块结构内部的节点联系非常紧密，而不同模块结构的节点之间联系就稀疏得多.

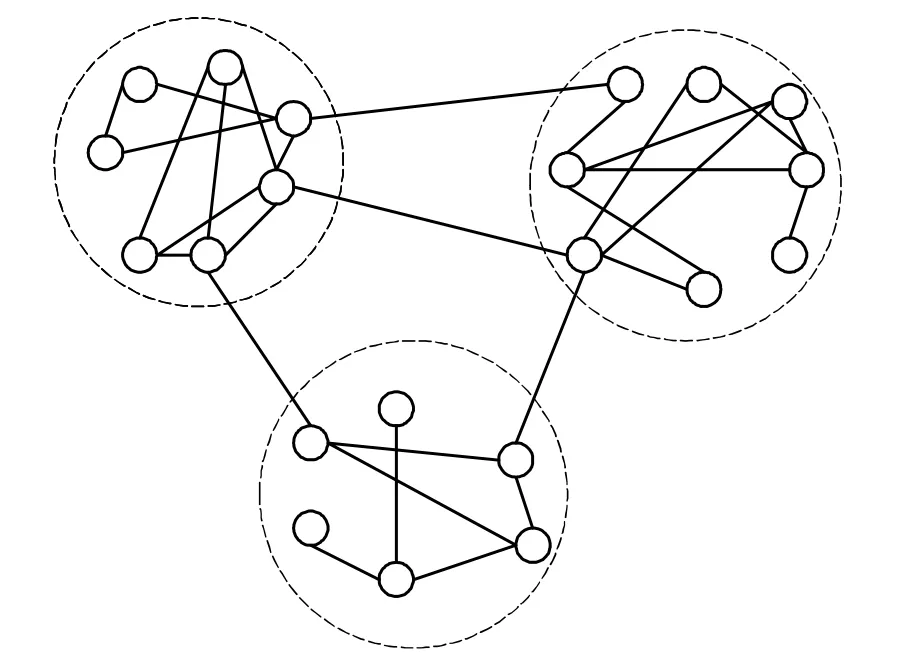
图1 小型模块结构网络示意图Fig.1 Schematic of a small network with modular structures

许多研究揭示了交通网络具有模块结构特性.文献［1］研究了世界航空网络中的模块结构;文献［5］基于艾哈迈达巴德等6个城市的交通网络拓扑结构，从统计学角度揭示了网络中的模块结构特性;文献［6］详细论证了中国铁路网络的加权特性以及网络中的模块结构.但是，这些研究成果只涉及交通网络模块结构的论证和描述，并未提出具体的城市路网模块结构划分和评价方法，难以体现出模块结构划分在交通规划与设计上的应用价值.

当前，复杂网络模块结构划分算法主要包括图形分割算法和分级聚类算法［7］.根据从网络中添加或删除边，分级聚类算法可分为凝聚算法和分裂算法.分裂算法以 GN(Girvan-Newman)算法［8］为代表，其准确性高，时间复杂度低，适合于中小型复杂网络.在GN算法中，为解决模块结构划分何时终止的问题，引进了一个衡量网络划分质量的标准——模块度.为了使GN算法能应用于大规模复杂网络，在GN算法的基础上进行了多种改进［9-13］，但只是改进了算法实现规则，并未对模块度函数进行更深入的研究.目前尚未见到城市路网模块度的相关研究.

以上算法和模块度研究的对象都是无权无向的抽象复杂网络，研究方向主要侧重于网络拓扑结构方面，尚未考虑实际交通网络的特性，例如，流量和流向分布、用户对路径的选择等.因此，这些算法和模块度函数不能直接应用于城市路网.

Hub路段是指那些一旦失效就会导致其他路段相继失效，进而产生连锁反应，最终导致整个路网瘫痪的关键路段，这种由Hub路段失效引起的路网瘫痪现象称为路网的级联失效.如何识别路网中的Hub路段并进行应急处理，已成为级联失效研究中的关键问题.为评价路段的重要性，文献［14］提出了一种基于路段选择概率的路段重要性评价方法;文献［15］指出应从路段失效的后果来评价路段重要性.以上方法对确定路段重要性都具有重要的理论和实际意义，但这些方法只考虑了路段失效后对流量分布造成的影响，并没有详细考虑路网的拓扑结构特性所起的作用.

本文基于GN算法思想，结合城市交通网络的特点，考虑路段权重和阻抗、交通流向和出行者的出行选择行为等特征，提出一种适用于城市路网模块结构划分及Hub路段诊断的算法——GN-T算法.该算法通过逐条移除介值最大的路段实现模块结构的划分，从而诊断出路网中的Hub路段，其中，各路段的介值在每次移除后需要重新计算.同时，为确定路网模块结构的最佳数量，提出了一个改进的模块度函数，并以武昌城市路网为例对算法的有效性进行验证.结果表明GN-T算法能较准确地探测出路网中的模块结构并诊断出Hub路段.

1 GN-T算法

1.1 变量符号和术语定义

考虑有向城市路网G(N，A)，其中:N表示交叉口集合，A表示路段集合，且路段p∈A.O和D分别表示起点和终点集合，起点r∈O，终点s∈D.GN-T算法的主要变量符号和术语定义如下:

(1)Bp为路段介数，即路网中所有OD对之间的最短路径通过路段p的次数.

(2)wp为路段权重系数，表示不同等级和方向的路段p在路网中的相对作用大小.

(3)cp为路段介值，表示路段p的介数与路段权重系数的乘积.

(4)wij为模块结构i与j之间所有路段权重系数的平均值.

(5)wii为模块结构i内所有路段权重系数的平均值.

(6)移除路段为算法每次迭代结果中介值最大的路段，也是路网中最有可能发生堵塞的路段.

(7)移除路段的顺序是算法在每次迭代过程中介值最大的路段依次被移除的顺序，移除路段的顺序越靠前表明该路段在路网中越容易堵塞.

1.2 算法原理

城市路网由不同的模块结构组成，连接各模块结构的路段称为连接路段.

由于不同模块结构的节点之间的最短路必经过连接路段，因此，连接路段将比模块结构内的路段具有更大的介值，介值越大，表明各OD对之间的最短路径通过该路段次数越多，通过该路段的交通量就可能越大，饱和度也越高，该路段也就更容易发生交通堵塞，在路网中的重要程度也越大.通过逐步移除这些介值最大的路段，可以将路网分割成不同的子网，即模块结构，而这些移除的路段很可能就是路网中的Hub路段.在城市路网中，快速路和主干路用于连接不同的区域，其路段交通量较大、饱和度较高、交通堵塞频繁发生，极有可能成为路网中的Hub路段.

1.3 算法流程

基于GN-T算法，采用C++编写了算法程序，并用JAVA语言编制了应用软件.

算法基本流程的步骤如下:

(1)程序初始化，读取节点坐标文件，得出城市路网的拓扑结构图;

(2)读取阻抗矩阵T，其中tp表示路段p上的阻抗，路阻函数采用BPR函数;

(3)读取路段权重系数矩阵W，其中wp表示路段p的权重系数;

(4)利用广度优先搜索算法求得任意OD对之间的最短路径，获得每个 OD对的最短路矩阵S;

(5)根据路段介数的定义，利用已经获得的最短路径矩阵S求出各路段p的介数Bp;

(6)计算各路段介值cp，移除路网中介值最大的路段;

(7)计算城市路网模块度函数，求得此时路网的模块度Q;

(8)获得模块结构数目N后，转步骤(2)，读取路网中更新的阻抗矩阵T和路段权重系数矩阵W;

(9)若路网中还有路段未被移除，转步骤(2);否则，转步骤(10);

(10)根据模块度Q，获得模块度与模块个数的关系变化图以及城市路网分块图，算法结束.

1.4 算法关键点

由于算法的实现较为复杂，下面对算法中的几个关键点进行详细说明:

(1)路段介数的计算通过广度优先搜索算法实现.假设在每个时间点，所有OD对之间有1个单位的流量产生，且交通分配服从用户均衡原则.根据所有OD对间的最短路计算路段介数和介值，将介值最大的路段从路网中移除，从而得到少了一条路段的新路网.在新路网中，OD需求不变，交通需求重新分配，路段介数和介值也重新计算，新一轮计算结果中介值最大的路段也被删去，如此类推，直到各个交叉口相互分离为止.

(2)路段介数可以理解为路段流量，而权重系数反映的是该路段在路网中所起作用的大小.本文把快速路单向3车道的通行能力归一化为1，作为标准权重系数，把主干路单向的通行能力、次干路单向的通行能力、支路单向的通行能力与快速路单向3车道的通行能力的比值作为各自的权重系数.

(3)路段介值定义为路段介数和权重系数的乘积，不仅体现了流量的作用，还考虑了路网拓扑结构的影响.例如，在城市路网中，某轮搜索得出介数最大的路段为一条单向2车道的快速路路段，其介数为 2400，权重系数为0.67，通行能力为3600 pcu;介数第2的路段为一条单向3车道的主干路路段，其介数为2100，权重系数为0.83，通行能力为3000 pcu.如果以介数直接作为路段重要程度的评判标准，就应把快速路删去，但此时快速路的饱和度为0.67，主干路的饱和度为0.70，主干路堵塞程度更严重，则应删去主干路.如果考虑路网拓扑结构，即加入路段的权重系数，以介值作为路段重要程度的标准，则快速路的介值为1608，主干路的介值为1743，显然主干路比快速路重要，应删去主干路，这与前面由路段饱和度得出的结论是一致的.因此，介值从流量和路网拓扑结构两方面反映出路段的重要程度，更符合实际情况.

2 改进的模块度函数

为了获得最优的城市路网模块结构数量，本文结合城市路网自身的特点，加入路段权重系数矩阵，对模块度函数进行了改进，以对城市路网模块结构划分的优劣进行评判.

假设城市路网划分为k个模块结构，定义两个k×k维的对称矩阵:

式中:eij为网络中连接两个不同模块结构i和j中节点的路段数占所有路段数的比例;

其中:n为连接模块结构i和j之间的路段编号;

q为连接模块结构i与j之间的路段总数(包括原始路网中的所有路段，不考虑是否被移除，即模块度是根据完整的原始路网来计算的).

定义每行(列)中各元素与对应路段平均权重系数的乘积之和为

式中:

Ai为连接模块结构i中节点与模块结构j中节点的路段数占所有路段数的比例.

定义模块度为

式(5)表示网络中连接两个同类型节点的路段(模块结构内部路段)的比例与同样模块结构下任意连接这两个节点的路段的期望值之间的差值.如果模块结构内部路段数的比例不大于任意连接时的期望值，则Q=0.Q的上限为1，Q越大，说明城市路网的模块结构越显著.文献［8］的研究表明，Q最大时所对应的模块结构数就是网络中最优的模块结构数.在实际网络中，Q值通常位于0.3 ～0.7 之间.

3 实例分析

本文选取武汉市武昌区交通网络进行实证研究.把信号交叉口抽象为节点，交叉口之间的路段抽象为边，用AutoCAD2007绘制出2011年武昌主城区内部交通网络系统图.该路网由快速路、主干路、次干路和支路构成，如图2所示.其中，路网节点总数为238个，边总数为984条.

调查得到了武昌区路网中不同等级道路的车道数、设计车速及单车道实际通行能力数据，见表1.

根据表1数据，把某单向3车道快速路的通行能力进行标准化处理，作为快速路路段的权重系数;其他道路路段通行能力与该快速路通行能力的比值作为路段权重系数，计算结果见表2.

在软件中导入节点坐标文件、时间矩阵文件和路段权重系数矩阵文件，程序运行结果如图3、图4和表3所示.

武昌城市路网模块结构划分的结果如图4所示.图4中红色线段表示的的路段就是路网中被移除的路段，通过移除这些路段就可以划分出路网的模块结构.对应的用AutoCAD2007绘制的模块结构划分效果图如图5所示.

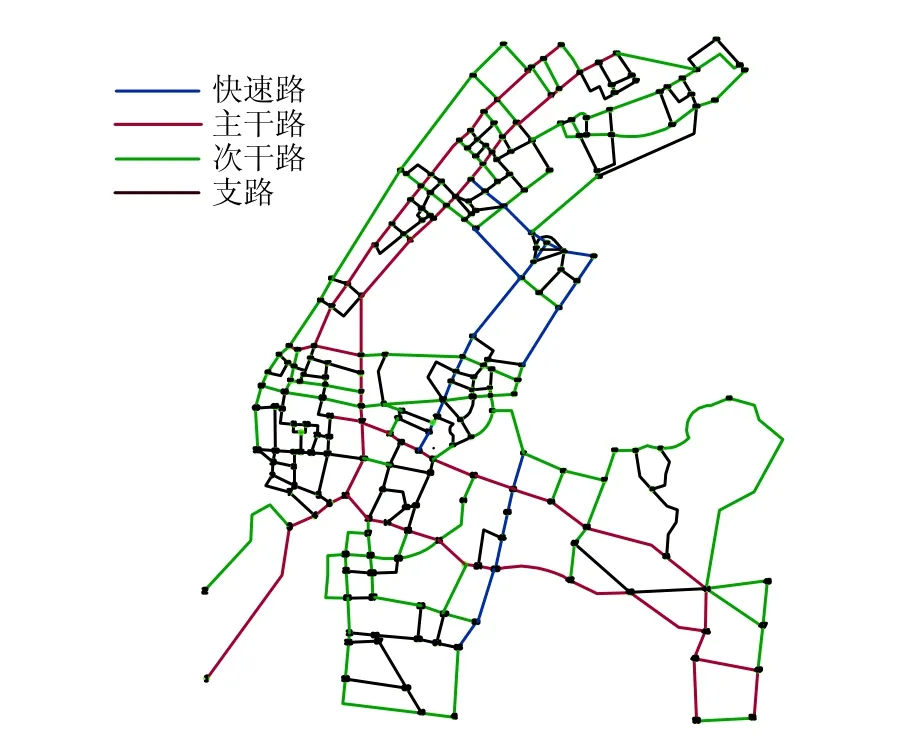
图2 2011年武昌主城内部交通网络图Fig.2 Map of Wuchang urban traffic network in 2011

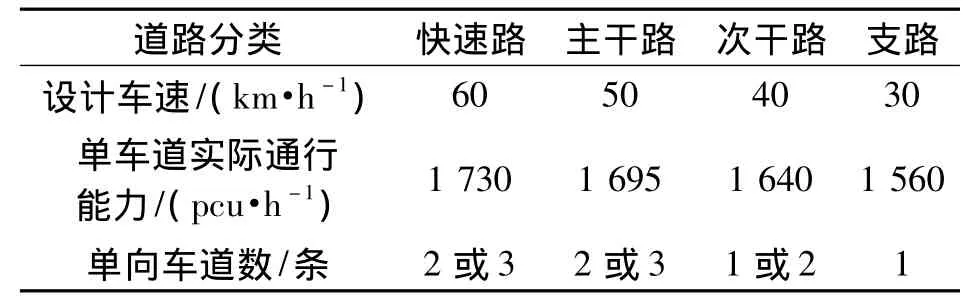
表1 武昌各等级道路属性Tab.1 Properties of roads of different grades in Wuchang urban traffic network

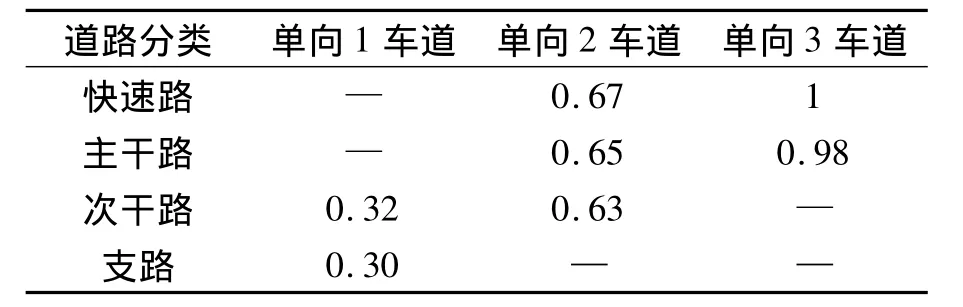
表2 武昌各等级道路路段权重系数Tab.2 Weight coefficients of roads of different grades in Wuchang urban traffic network

图3 模块度-模块结构数曲线Fig.3 Modularity vs.number of modular structures

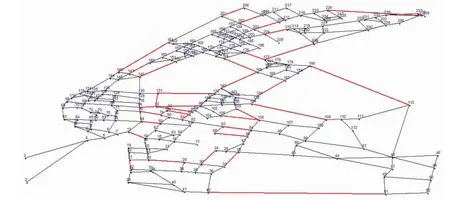
图4 结果图及移除路段Fig.4 The resultant map and removed links

表3 路网中移除的路段(Hub路段)及顺序Tab.3 The removed links(hub links)and their removal order

根据GN-T算法原理，移除的路段很可能就是武昌城市路网中的Hub路段，在程序运行过程中移除的路段和顺序见表3.根据调查所得资料显示，表3中带有#的路段均为武昌城市路网中的快速路和主干路，是武昌城市路网中的关键路段.目前这些路段经常处于堵塞状态，特别是在出行高峰期间，这些路段均出现不同程度的堵塞，而且与其连接的路段也由于受到波及而进入堵塞状态.

在最严重的情况下，武昌路网中接近四分之一的交叉口处于短时瘫痪状态.而没有标记的路段均为主干路或次干路，路段饱和度均为0.8左右，在高峰期间也会陷入短时堵塞状态.究其原因是目前这些路段交通流过大，非机动车及行人交通在交叉口和路段中违法穿插，加之地铁或道路施工使得某些路段封闭了近一半的车道、信号交叉口控制不协调等原因进一步降低了路段和交叉口的通行能力，导致交通供需不平衡，从而引起车辆排队堵塞.

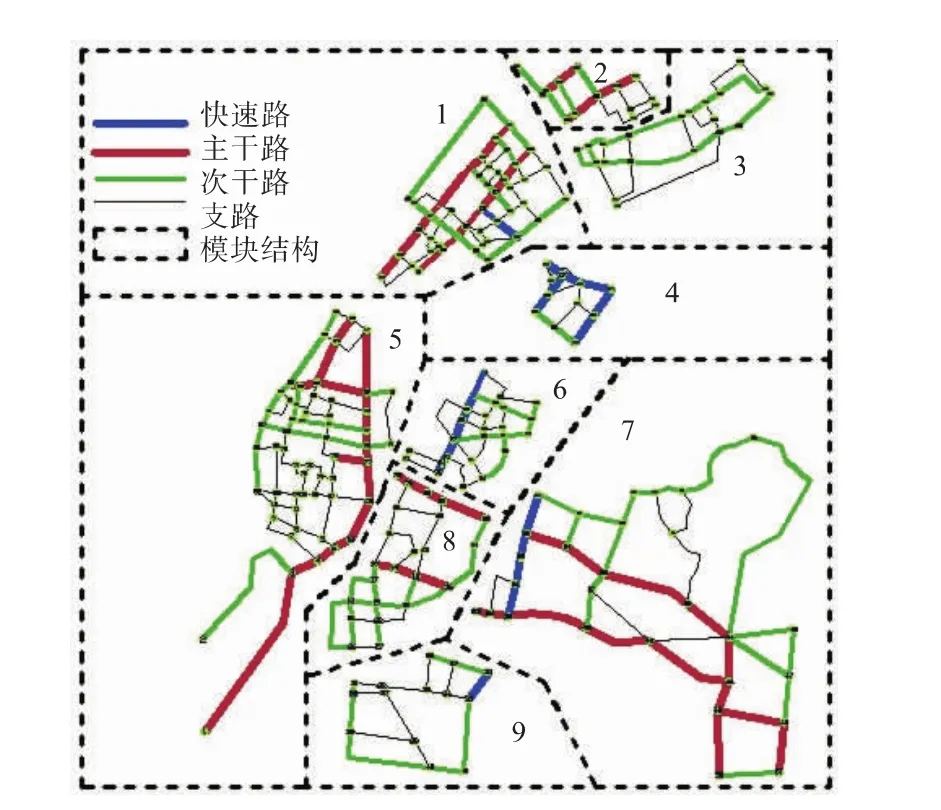
图5 9个模块结构Fig.5 Nine modular structures

从上述分析可以看出，GN-T算法所得的结果与实际情况基本相符，该算法能够较准确地诊断出武昌城市路网中的Hub路段，说明该算法在实际应用中是有效的.

4 结束语

本文基于复杂网络模块结构理论，结合城市路网的特点和运行特性，提出了划分城市路网模块结构的GN-T算法，并应用于武昌城市路网模块结构探测及Hub路段诊断中.程序运行所得结果表明，武昌城市路网表现出较明显的模块结构特性，该算法诊断出的武昌城市路网中的Hub路段与实际情况相符，验证了GN-T算法适用于划分该路网的模块结构.

揭示复杂网络中的模块结构已成为理解网络功能的有力工具.在对城市路网模块结构进行了有效划分并诊断出Hub路段后，应对路网拓扑结构与网络功能之间的关系作进一步探究，以更好地掌握城市交通运行机理，揭示城市路网级联失效过程的机理，并做出相应的应急处理方案，这将是未来的研究方向.

［1］GUIMERA R，MOSSA S，TURTSCHI A，et al.The world-wide air transportation network:anomalous centrality， community structure， and cities'global roles［C］∥ Proceedings of the National Academy of Sciences USA.Washington D.C.:［s.n.］，2005:7794-7799.

［2］卢守峰，杨兆升，刘喜敏.基于复杂性理论的城市交通系统研究［J］.吉林大学学报:工学版，2006，36(3):153-156.LU Shoufeng，YANG Zhaosheng，LIU Ximin.Research on urban traffic system based on complexity theory［J］.Journal of Jilin University:Engineering and Technology Edition，2006，36(3):153-156.

［3］SEN P，DASGUPTA S，CHATTERJEE A，et al.Small world properties of the Indian railway network［J］.Physical Review E，2003，67:036106.

［4］SIENKIEWICZ J，HOLYST J A.Statistical analysis of 22 public transport networks in Poland［J］.Physical Review E，2005，72:046127.

［5］PORTA S，CRUCITTI P，LATORA V.The network analysis of urban streets:a dualapproach［J］.Environment and Planning B:Planning and Design，2006，33(5):705-725.

［6］LI X G，GAO Z Y，LI K P，et al.The relationship between microscopic dynamics in traffic flow and complexity in network［J］.Physical Review E，2007，76:016110.

［7］汪小帆，陈关荣，李翔.复杂网络理论及其应用［M］.北京:清华大学出版社，2006:156-162.

［8］NEWMAN M E J，GIRVAN M.Finding and evaluating community structure in networks［J］.Physical Review E，2004，69:026113.

［9］RADICCHI F，CASTELLANO C，CECCONI F，et al.Defining and identifying communities in networks［J］.Proc.Natl.Acad.Sci.，2004，101:2658-2663.

［10］CLAUSET A，NEWMAN M E J，MOORE C.Finding community structure networks［J］.Physical Review E，2004，70:066111.

［11］CAPOCCI A，SERVEDIO V D P，CALDARELLI G，et al.Detecting communities in large networks［J］.Computer Science，2004，3243:181-187.

［12］FORTUNATE S，LATORA V，MARICHIORI M.A method to find community structures based on information centrality［J］.Physical Review E，2004，70:056104.

［13］DUCH J， ARENASA. Community detection in complex networks using extreme optimization［J］.Physical Review E，2005:72:027104.

［14］TAYLOR M A P，D'ESTE G M.Critical infrastructure and transport network vulnerability:developing a method for diagnosis and assessment［C］∥Proceedings of the Second International Symposium on Transportation Network Reliability (INSTR).Christchurch:［s.n.］，2004:96-102.

［15］JENELIUS E，PERERSEN T， MATTSSON L G.Importance and exposure in road network vulnerability analysis［J］.Transportation Research Part A，2006，40:537-560.