涡轮转子榫结构单侧偏差对应力影响的分析

王 沛，杜 强，冯笑男，黄恩亮，尹 娟，朱俊强

(1.中国科学院工程热物理研究所，北京 100190;2.中国科学院大学，北京 100190)

为了能有效减少叶片向盘体的传热、降低整体叶片盘的加工难度并提高零件的可维修性，同时考虑到发动机对叶片/盘不同的材料性能要求，榫接结构在先进航空发动机的压气机、涡轮部件中得到了广泛应用。然而，实际工作状态下，涡轮部件普遍在高温、高压、高转速的恶劣环境下运行，工作条件复杂，这将导致榫接结构位置处存在较严重的应力集中现象，内部应力状态也非常复杂，成为涡轮故障多发环节之一。据统计，涡轮故障中高达20%的故障是由于榫头、榫槽结构失效而造成的［1］。因此榫齿结构作为叶片重要考核部位，成为国内外学者广泛研究的对象［2］，榫接结构优化设计、强度寿命校核等方面的研究工作正在深入展开［3-10］。

而在实际加工制造过程中，受加工工艺、加工设备(拉刀、加工工装)及其准备状态的影响，榫头、榫槽的齿型与设计状态往往存在一定的偏差，这将导致榫接结构处的接触情况发生改变，进而造成榫接结构应力分布发生变化。因此对实际加工造成的齿型几何偏差(非设计状态)开展细致的强度分析，便逐渐引起了研究人员的关注。这对榫连接齿型公差设计具有重要意义［11］，作为航空发动机涡轮转子榫齿裂纹产生原因之一，也是故障分析的重点关注方向［12］。

同时也发现，相关研究普遍基于中心对称榫齿模型开展。而实际情况下，受加工精度影响，对称度难以保证。单侧榫连接接触面偏差对接触面、喉部应力分布的影响目前研究的较少。本文即以某高压涡轮盘(图1)为原型，建立单侧齿接触面存在偏差的榫接结构模型，进行有限元计算与分析。

图1 某高压涡轮盘

1 研究模型

研究对象为某高压涡轮两齿榫接结构。该高压涡轮叶片数为41。图2为该涡轮盘-叶片1/41循环对称三维实体模型。

图2 某涡轮盘-叶片1/41几何模型

两齿榫接结构二维截面几何模型见图3，相关参数见表1。

图3 两齿榫接结构几何模型

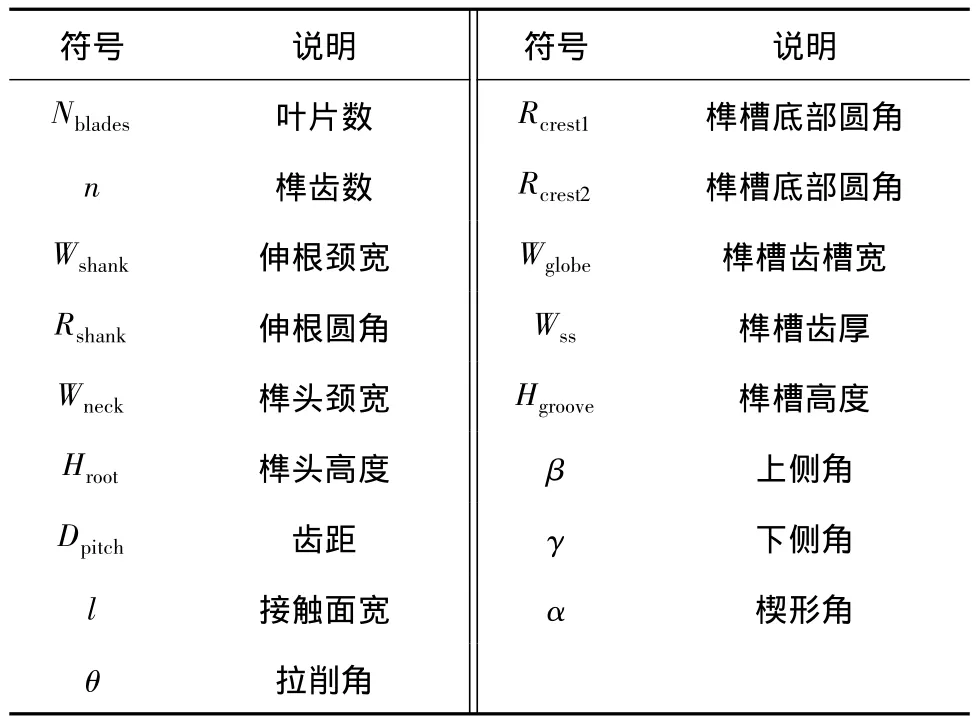
表1 推接结构的特征参数

为便于描述，榫接结构4个接触面按图4进行编号。本文以接触面2存在加工偏差为例，相比设计状态，榫头工作面不变，榫槽工作面向上偏移，偏移距离为 h。对 h=0(设计状态)、h=0.01 mm、h=0.02 mm、h=0.03 mm 等状态进行建模，考察单侧接触存在偏差对榫接结构工作应力的影响。

图4 榫接单侧齿偏差几何模型

2 数值求解方法

榫连接结构需求解接触问题，属于不定边界问题，且随着压力变化，接触面积及压力分布具有非线性，同时接触面间存在摩擦作用，因此接触问题具有表面非线性。由于表面非线性和边界不定性，求解接触问题复杂度较高，一般来说，需进行反复迭代求解［13］。

对存在接触的两个物体，根据虚功方程有:

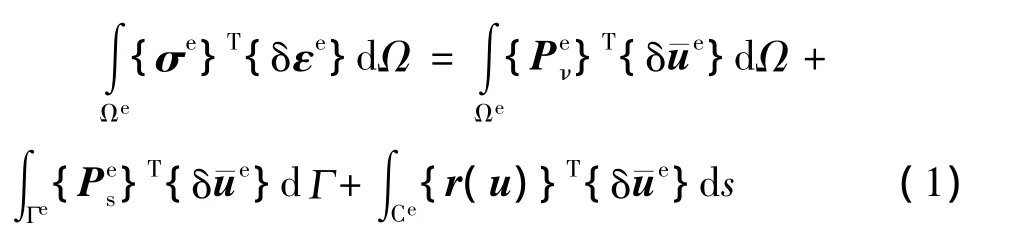
其接触约束算法采用罚函数法，即r(u)={P，τy，τz}，其中 P 为法向接触压力

接触设置采用法向硬接触、切向有限滑移方法。

榫头材料为K465，榫槽材料为GH500。相关材料属性见表2、表3。

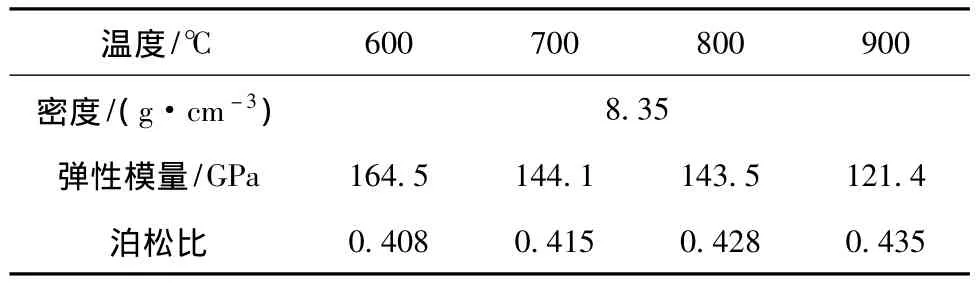
表2 K465材料属性

表3 GH500 材料属性［14］

为更准确获取榫连接结构应力分布，计算模型选用1/41周期的二维轴对称有限元模型。涡轮转子转速为38 600 r/min。叶片及盘心对榫连接结构的影响通过边界条件给出。在高转速下，叶片所受离心力通过伸根作用于榫头，此处等效为分布力σneck。为准确模拟盘心对榫连接的影响，特对涡轮盘-叶片1/41几何模型进行三维有限元计算，求得图5所示内缘处平均位移Ur，并作为位移约束施加于二维计算模型内缘处。模型按照带厚度平面应力分析方法求解，轴向长度为榫头厚度。相关计算边界条件设置如图5。另根据发动机空气系统结果及涡轮部件温度分布估算公式设置二维计算模型的温度场。按空气系统结果，高压涡轮盘盘心温度450℃，盘缘600℃，轮盘温度沿半径方向服从4次方分布规律(见公式(2))。叶片按气动计算结果，表面最高温度900℃，约在80%叶高处。模型温度设置如图6。

式中:R—涡轮盘上某点处半径;R0—涡轮盘心半径;Rk—涡轮盘缘半径;T—涡轮盘上某点处温度;T0—涡轮盘心温度;Tk—涡轮盘缘温度。

数值模拟软件选用 ANSYS。模型网格选取PLANE82类型，接触面为面-面接触，接触对网格类型为TARGEl69和CONTAl72。

图5 有限元计算边界条件设置

图6 模型温度设置

计算结果处理时，为了对应力水平进行直观评估，对榫接结构工作应力进行无量纲化处理(见公式(3))。

式中:［σ］—相对应力;σ—榫连接模型实际应力;σneck—参考应力为工作状态下，叶片截面A(见图5)以上部分产生的离心力。

3 网格收敛性考察

网格密度对有限元计算结果存在显著影响，为避免因网格导致的计算误差，建立了不同密度的有限元网格来考察接触应力的计算结果。以接触面四边形网格单元边长与接触区边缘圆角半径的比值Le/Rshank作为度量网格密度的参数。如图7所示，选取接触面上三个点A、B、C处的Von Mesis应力进行对比，考察不同密度的有限元网格［15］。

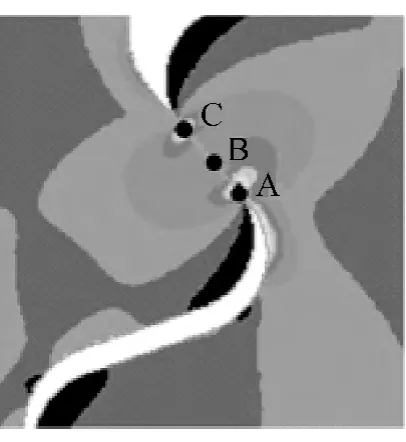
图7 接触面典型位置点选取示意图

表4给出了不同网格密度下A、B、C 3点的等效应力。随着网格密度增大，接触面边缘的应力值计算结果相应增大，且逐渐逼近。对比3点Von Mises应力发现，网格3与网格2的计算结果差距不超过3.6%，因此本文采用网格3作为有限元分析模型。

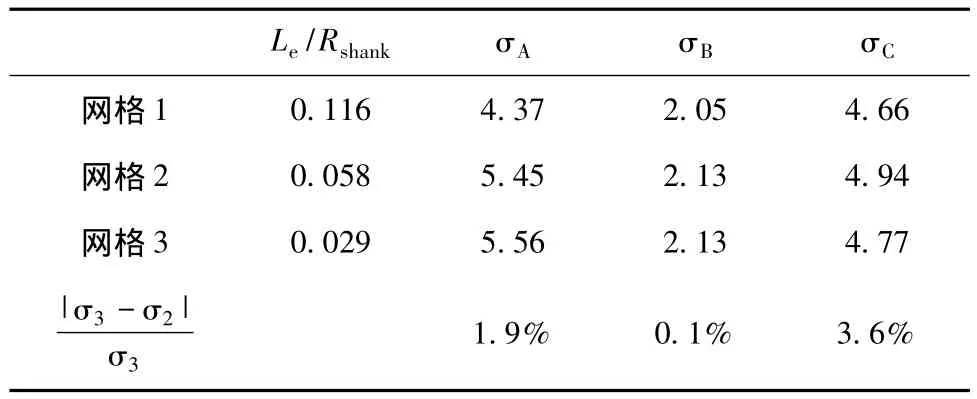
表4 不同网格密度模型应力计算结果

4 单侧接触面偏移对应力的影响

通过对比接触面2不同偏移值模型的计算结果，分析偏移值h与接触面处应力之间的关系。

图8(a)为设计状态下榫头榫槽应力分布。计算结果显示，应力分布几何对称。从应力值来看，最大应力点位于上侧榫齿接触面，相对应力为5.85。图8(b)、(c)、(d)分别为接触面 2偏移值 h为0.01 mm、0.02 mm、0.03 mm 时的应力分布。由图中来看，应力分布的对称性被打破，接触面2应力因加工偏差而减小，相应接触面4应力增大。由图8(b)，当单侧榫槽加工偏差0.01 mm时，应力最大点位于接触面4，相对应力为5.56，相比设计状态最大应力减小了5.0%。由图8(c)、(d)，当偏差h增大时，应力最大值也随之增大，相比设计状态最大应力，h=0.02 mm和h=0.03 mm的最大应力值分别增大16.4%和37.4%，应力集中更为严重。这将加剧发生涡轮盘榫齿故障中的裂纹、掉块和压剥落现象的概率。

h=0.01 mm时，最大应力与设计状态相当。随着接触面偏差增大，最大应力随之增大。

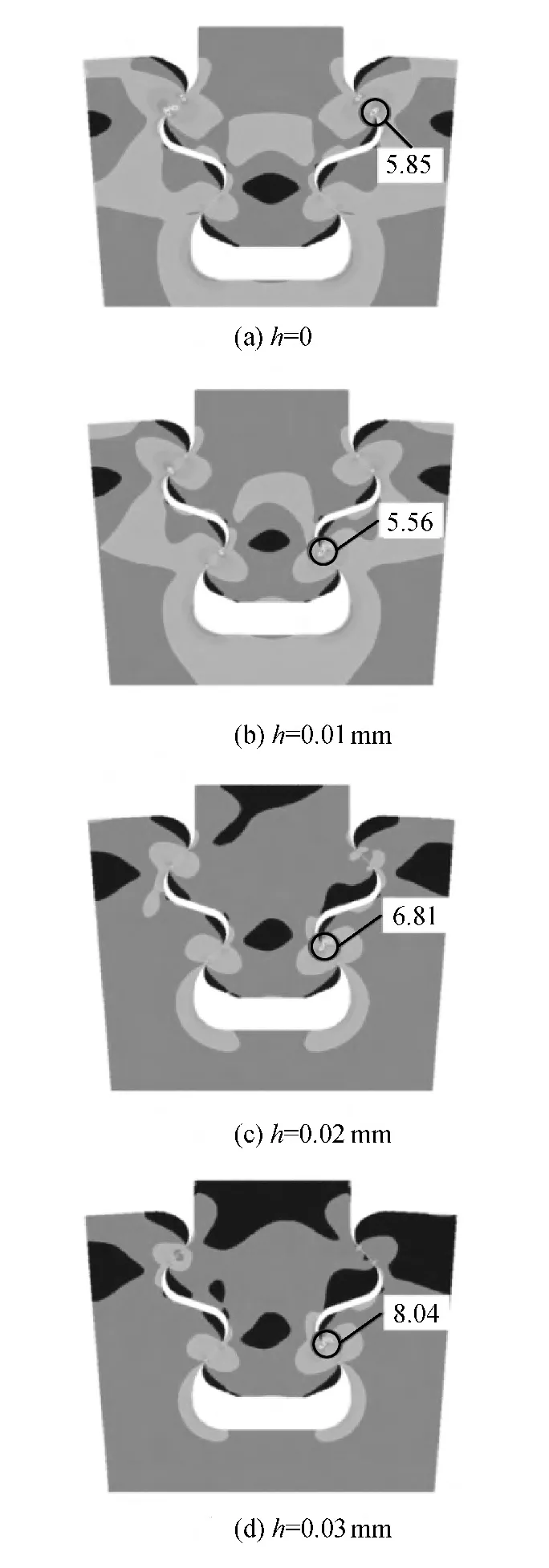
图8 不同间隙模型应力分布

图9～图12给出了不同h值下榫头接触面的Von Mises应力分布曲线。通过计算求得不同h值下榫头接触面平均相对应力，见表5。设计状态下，上侧榫齿接触面应力较下侧接触面应力大，这说明在工作状态下，上侧榫齿起到了主要的承载作用。当h=0.01 mm时，榫接结构工作应力对称分布被打破，接触面2应力小于接触面1，接触面4应力较接触面3大。比较图9～图12，随着h值增大，上侧接触面应力逐渐减小，下侧接触面应力逐渐增大，从应力变化幅值来看，接触面2应力显著减小，位于同侧的接触面4应力显著增大。

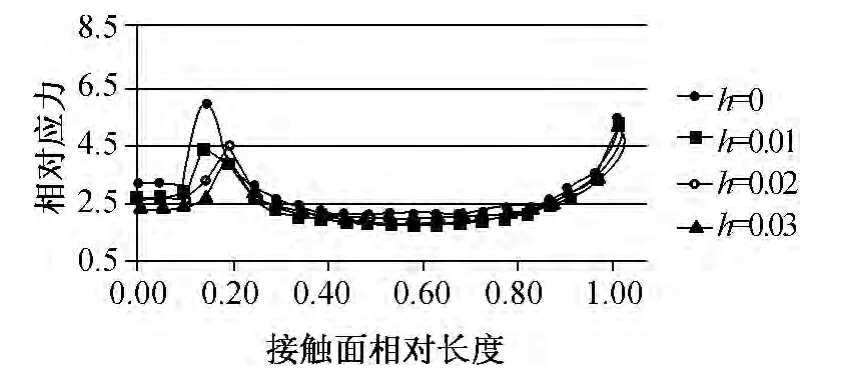
图9 接触面1相对应力分布

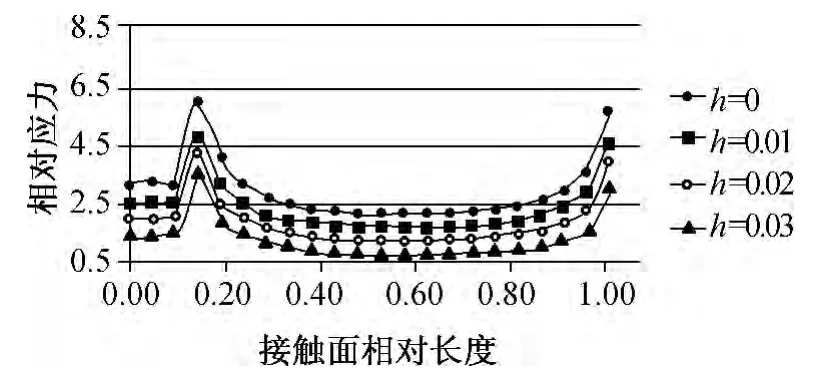
图10 接触面2相对应力分布

图11 接触面3相对应力分布

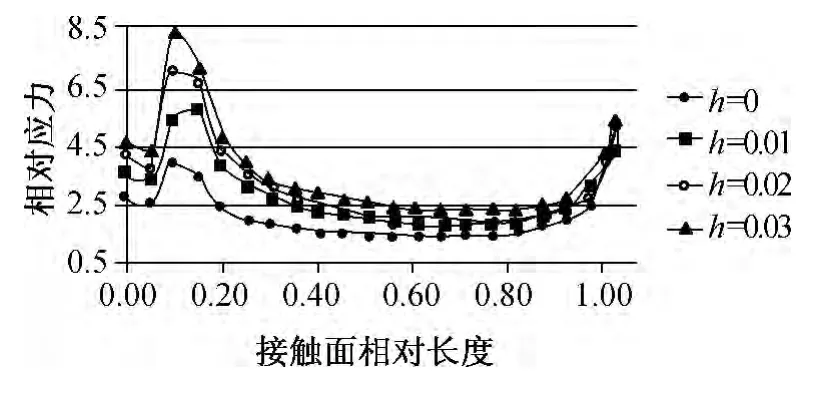
图12 接触面4相对应力分布

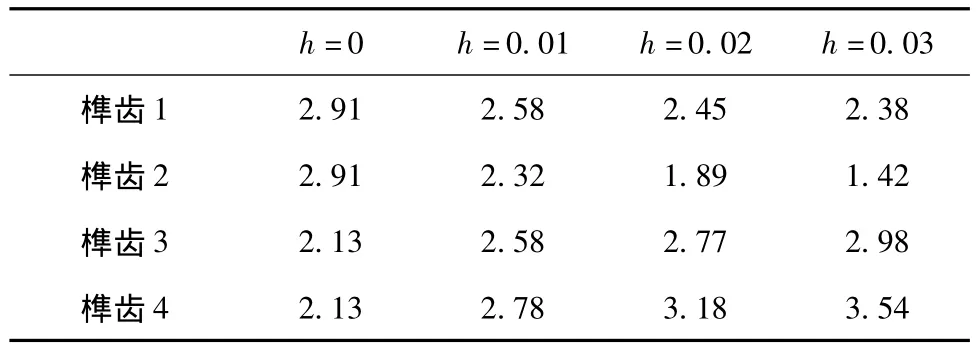
表5 不同h值下榫头接触面平均相对应力比较

5 榫头喉部径向应力比较

榫头喉部是榫接结构危险截面，其宽度较小，径向拉伸应力大，且存在应力集中现象，易导致榫连接疲劳失效。因4个接触面应力分布发生变化，喉部应力也会受到影响。图13给出了榫头喉部位置的相对径向应力分布。表6给出了不同h值下榫头喉部应力集中系数。由图可知，设计状态下，相对径向应力对称分布，在两侧边缘处出现应力集中现象，应力集中系数为3.41。当榫齿接触面单侧发生偏移时，喉部应力不再对称分布，远离接触面2一侧喉部应力变化不显著，而同侧的喉部应力随h值加大而增大。当 h=0.03 mm时，应力集中系数增大15.84%。相比设计状态，榫齿接触面单侧偏移导致榫头喉部承载水平加大，应力集中加剧。

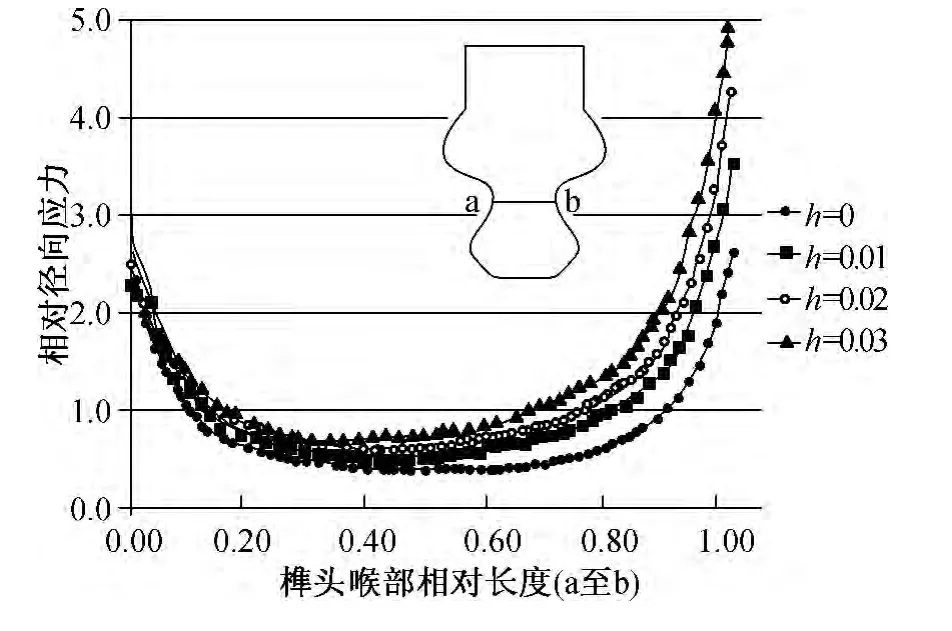
图13 榫头喉部相对径向应力曲线

表6 不同h值下榫头喉部应力集中系数比较

6 结论

本文以设计转速下某两齿榫接结构的应力水平评估为研究内容，着重对设计状态和单侧接触面存在偏差的状态(由加工误差造成)进行了二维有限元计算与对比，分析了接触面偏差值对各榫齿接触面处等效应力及喉部径向应力的影响，通过研究得出以下结论:

(1)榫连接单侧接触面发生较小的齿形偏差即会引起承载力不均，存在偏差的接触面应力减小，而同侧异齿处接触面应力增大，上侧榫接触面不再起主要承载作用。

(2)从接触面应力峰值来看，当榫齿接触面超差0.01 mm时，应力水平与设计状态相当，可认为是加工超差的允许值。而当超过0.01 mm后应力峰值明显升高，实际使用时容易出现微动疲劳。

(3)单侧榫接触齿型偏差导致喉部径向应力变化。在齿型偏差的同侧喉部应力集中情况更为严重，应力集中系数较设计状态最大增大了15.84%，而异侧应力变化并不显著。

［1］《航空发动机设计手册》总编委会.航空发动机设计手册:第10册［M］.北京:航空工业出版社.2001.

［2］孙瑞杰，闫晓军，聂景旭.定向凝固涡轮叶片高温低周疲劳的破坏特点［J］.航空学报，2011，32(2):337-343.

［3］孙瑞杰，闫晓军，聂景旭.基于复合疲劳试验的涡轮叶片振动应力反推法［J］.航空动力学报，2012，27(2):289-294.

［4］Oakley S Y，Nowell D.Prediction of the combined high-and-lowcycle fatigue performance of gas turbine blades after foreign object damage［J］.Int.J.Fatigue，2007，29(1):69-80.

［5］申秀丽，齐晓东，王荣桥，等.航空发动机涡轮榫接结构齿形基本参数研究［J］.航空动力学报，2011，26(4):735-744.

［6］Meguid S A，Kanth P S，Czekanski A.Finite element analysis of fir-tree region in turbine discs［J］.Finite Element Analysis and Design，2000，35(4):305-317.

［7］Song W，Keane A，Rees J，et al.Turbine blade fir-tree root design optimisation using intelligent CAD and finite element analysis［J］.Computer and Structures，2002，80(24):1853-1867.

［8］赵海.涡轮榫头/榫槽结构设计方法研究［D］.南京:南京航空航天大学，2005.

［9］温卫东，高德平.榫头/榫槽接触问题边界元分析［J］.航空动力学报，1992，7(2):117-120，192.

［10］魏大盛，王延荣.榫连结构接触面几何构形对接触区应力分布的影响［J］.航空动力学报，2010，25(2):407-411.

［11］马安新，王三民，吕文林，等.几何尺寸误差对盘片接触系统强度影响研究［J］.航空动力学报，2001，20(3):369-370.

［12］郑旭东，蔚夺魁，王兆丰，等.某型航空发动机涡轮叶片和轮盘榫齿裂纹故障力学分析［J］.航空发动机，2005，31(3):35-38.

［13］K.L.Johnson.接触力学［M］.北京:高等教育出版社.1992.

［14］《中国航空材料手册》编辑委员会.中国航空材料手册［M］.北京:中国标准出版社.2002.

［15］YANG Xiaojie，DU Qiang，ZHU Junqiang.Fir-tree tenon/mortise structure design under real aero-engine turbine environment based on UG and ANSYS［R］.ACGT2012-8131，2012.