航空发动机热端部件二次流动和传热耦合方法研究
2014-07-14郭晓杰竺晓程杜朝辉
郭晓杰,顾 伟,竺晓程,杜朝辉
(1.上海交通大学工程热物理研究所,上海 200240;2.中航商用航空发动机有限责任公司,上海 200241)
航空燃气涡轮发动机空气系统是由发动机零部件上的一系列管路、孔、篦齿、缝等流阻元件组成流路网络系统,也称为二次流,其主要功能是从压气机等位置抽取一定量的气体,用于热端部件冷却、轴承腔封严、轴向力平衡、防冰等。空气系统计算的方法是,根据建立的流路网络系统,设计合适尺寸的元件,实现空气系统的功能。热端部件传热分析的目的是获得零部件的温度场,为强度计算提供输入。传热分析的关键是根据零部件所处的气流流动环境,计算传热边界条件。
零部件所处的气流环境包括燃气和二次流,空气系统计算为零部件热分析提供关键的二次流动传热边界。同时,零部件的温度场反过来又影响到空气系统沿程气流的温升、压力及流量分布。因此,二次流计算和部件热分析在物理机理上是耦合的。但目前在工程上,空气系统计算和热端部件的热分析,两者是解耦分析的,手工进行迭代计算。这样的方法效率低下,精度也不高,特别是对于空气系统沿程温升的计算,在空气系统设计中一直是个难题,目前普遍的方法是根据经验人工给出数值,最终导致空气系统和温度场计算结果有所偏差。因此,迫切需要将空气系统计算和零部件热分析进行耦合,提升计算效率和精度。在国内外研究中,郭文[1]、陶智[2]等采用流-热耦合方法对空气系统进行计算分析;Muller[3]对空气系统和部件进行耦合方法研究,获得与实验结果更加吻合的耦合计算结果。
流-热耦合计算方法主要分为两种:一种是强耦合计算,该类耦合计算流体域和固体域采用同一求解器,通过计算包含所需物理量的单元矩阵进行耦合分析,一次求解就能得出耦合场的分析结果[4-5];而另一种则是弱耦合计算,该类耦合计算分别对流体与固体域采用单独的求解器,通过将前一个分析的结果作为载荷施加到下一个分析中的方式进行耦合,需要反复迭代得到分析结果[6-7]。
本文中,空气系统采用稳态流路网络计算方法,热端部件热分析则采用有限元计算方法,将空气系统计算和温度场分析通过弱耦合的流-热耦合方法结合起来,获得更为准确的空气系统和温度场计算结果,对工程应用具有非常重要的意义。
1 空气系统计算与部件热分析的耦合方法
1.1 空气系统计算[8]
空气系统的计算采用流路网络法,将二次空气流路简化为由流体单元和节点组成的网络,采用流量平衡残差进行腔室压力校正,能量平衡进行腔室温度计算。
图1中,表示了彼此联系的4 个腔室 i、j、k、l所组成的局部空气网络,腔i与3个分支相联系,mij、mik、mil分别为3个分支的流量。
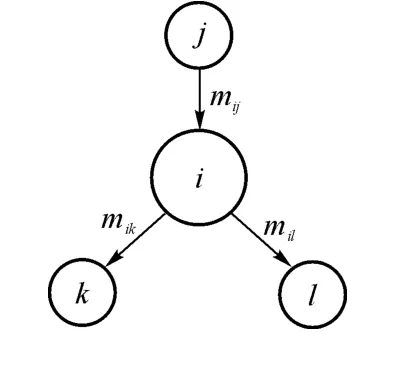
图1 网络模型
腔室压力的修正是基于质量守恒定律,对于N个腔室和M个分支,每个腔室都可以写出压力校正方程:

根据求得的压力校正量ΔPi,即可得到新的腔室压力:

腔室温度的计算是基于能量平衡的原理,对于每个腔室的冷却空气混合温度有:

工程上,若不进行二次流动与传热的耦合分析,单独对空气系统进行计算时,冷却空气的温升则是根据经验取某一数值,并未进行精确的计算。
1.2 热端部件热分析
流-热耦合计算时,热端部件的热分析采用有限元方法进行,其基本原理是将热分析对象离散成有限个单元,通过单元上的节点相互联结成一个组合体,同时将连续分布的温度也离散为有限个温度值,根据能量守恒原理,对一定边界和初始条件下的单元节点的热平衡方程进行求解,得到各个节点的温度值,进而求解出其他相关参数。
本文中,热端部件的热分析采用大型通用有限元分析软件ANSYS进行。通过ANSYS的二次开发功能-APDL,实现热端部件热分析的自动进行。
1.3 流-热耦合方法
空气系统和热端部件之间的对流换热,是部件表面与其冷却空气之间存在温差引起的热量交换。对每一个腔室,由牛顿冷却方程,则有:

式中:h为冷气与壁面的换热系数,A为冷气与壁面的换热面积,Tw为固体壁面平均温度,Tc为冷气的平均温度。
冷却空气的平均温度取其进出口处温度的算术平均值,则:

若壁面与冷却空气的换热量被冷气全部吸收,则腔内冷却空气温度的变化为:

将由公式(6)~公式(8)所得到的冷气温升,结合公式(1)~公式(5),即可得到经过对流换热后,腔室中冷气的温度。
空气系统和热端部件的流-热耦合计算流程如图2所示,具体过程为:
(1)给定进出口边界,设定腔室压力和腔室温度初值,进行空气系统计算(此时没有考虑部件对冷却空气的传热)。
(2)将计算所得的流体参数(压力P、温度Tc、流量m)传递给传热边界计算程序,计算部件热分析边界条件,并将计算所得边界条件(换热系数h及流体温度Tc)传递给热端部件。
(3)用从(2)获得的换热边界对所建立的热分析文件进行修改,调用ANSYS程序进行部件温度场计算,获得热分析结果,输出流体与热端部件换热壁面的温度值Tw。
(4)根据从(3)所得壁温Tw,通过冷气温升计算程序,计算出冷却空气的温升ΔT,并传递给空气系统计算程序。
(5)空气系统再次计算,返回(2)不断循环迭代,直到满足某一计算精度为止。
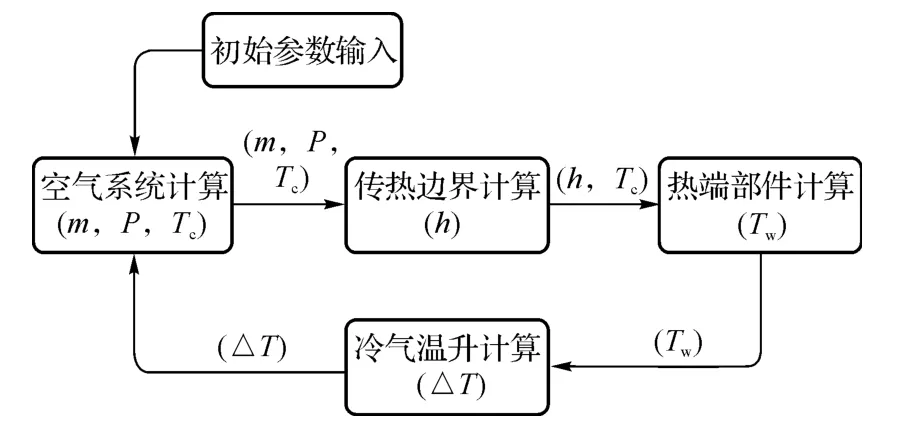
图2 耦合迭代计算流程示意图
1.4 耦合计算的实现
空气系统和热端部件流-热耦合计算过程的实现是基于VB开发语言及ANSYS的APDL二次开发。
结合ANSYS的APDL二次开发,建立高温部件的二维稳态热分析的命令流文件,以方便在耦合迭代过程中的程序调用。基于VB,进行传热边界计算模块和冷气温升计算模块开发,其中传热边界计算中的换热系数来自实验及经验关系式。
在已有的空气系统计算程序基础上,利用VB实现空气系统计算程序和热端部件热分析软件以及相关模块的调用,并实现整个迭代过程中的相关数据的传递,完成空气系统和热端部件的流-热耦合迭代计算。
2 算例分析
2.1 计算模型
某型发动机高压涡轮机匣二维结构模型如图3所示,涡轮机匣的下表面为主燃气通道,从燃烧室喷出的高温燃气,使得机匣一直在较高的热负荷下工作。因此从发动机其他位置引入二次流对机匣进行冷却,保证其能可靠地工作。图3高压涡轮机匣结构中所示线路,为冷却空气的两条流动路线。空气系统流路中有2个冷气进口和7个冷气出口,冷气流经机匣各个腔室,对高温零部件进行冷却。第一条冷却流路,从燃烧室外环引入冷却空气,经进口1进入机匣腔内。其中分支B对高压涡轮一级导叶缘板进行冷却,经出口1流出;分支D对高压涡轮一级动叶外环进行冷却,经出口3进入主燃气通道。第二条冷却流路,从压气机七级引气,经进口2进入机匣腔内。其中,分支H对高压涡轮二级导叶缘板进行冷却,经出口5流出;分支J对高压涡轮二级动叶外环进行冷却,经出口7进入主燃气通道。
在耦合计算分析时,空气系统采用流路网络法进行计算。图4为高压涡轮机匣的冷却空气流路网络图,进出口和分支编号与图3中所标示的流路编号相对应。
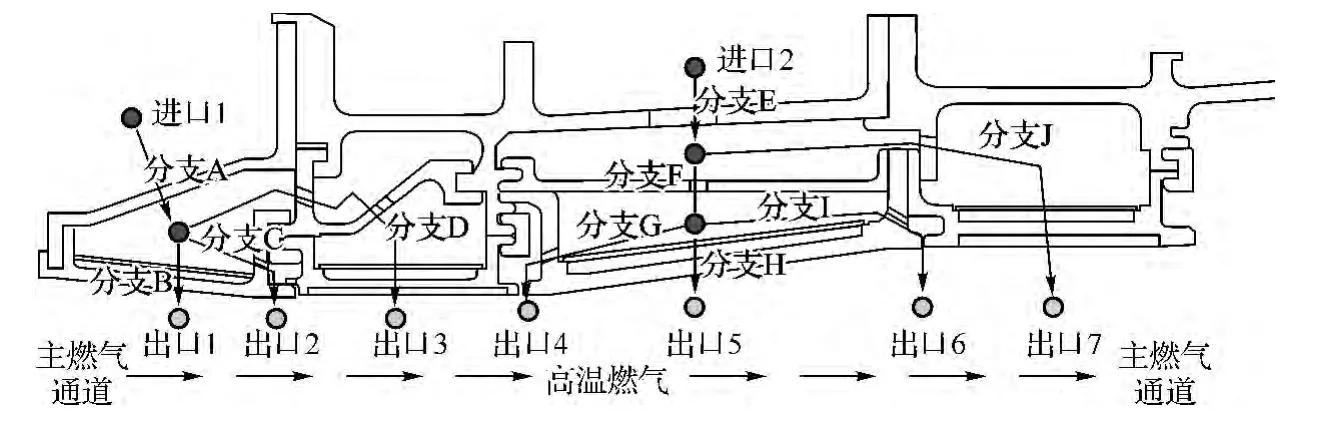
图3 机匣物理模型及冷却流路
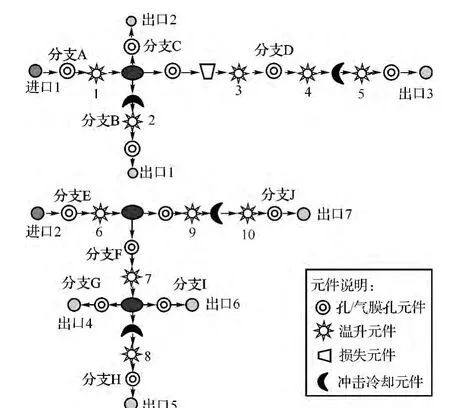
图4 空气系统网络图
高压涡轮机匣热分析则采用二维轴对称有限元方法进行计算。机匣计算模型进行了适当的结构简化,选择 PLANE55(Thermal Solid,Quad 4node 55)二维轴对称的单元类型进行稳态热分析,采用四边形网格作为网格单元形状,采用自由网格划分作为网格划分的类型,共有约1.1万个网格单元,如图5所示。
2.2 边界设置
空气系统的边界条件需要给定冷气流路的进出口压力和温度。表1和表2为参考某发动机压气机和主燃气通道参数所假定的空气系统进出口边界条件。
文中所涉及到的流量、压力、温度参数均采用无量纲量,其中无量纲流量:

式中:m为当地流量,W25为高压压气机进口流量。

图5 高压涡轮机匣计算模型
无量纲压力:

式中:P为出口静压,Pt为高压压气机出口总压。
无量纲温度:

式中:T*为出口总温,T*t为高压压气机出口总温。

表1 进口边界条件

表2 出口边界条件
高压涡轮机匣的换热边界计算均采用相应的经验公式进行。机匣的热分析的边界加载位置如图6所示,其中机匣下表面流经高温燃气,1~4位置处的换热系数和流体温度直接取燃气参数,按照相应的经验公式计算获得;机匣上表面为流动的微弱区域,16~18位置处取相应的经验值加载对流边界;其余区域为冷却空气的流动区域,5~15位置处按照冷却方式,取相应的换热经验公式进行处理,冷气参数由空气系统计算获得。
2.3 空气系统计算结果
图4中,温升元件1~10所在腔为冷却空气和热端部件发生耦合传热的主要腔室。对元件1~10所在腔室,对比分析非耦合计算和耦合计算结果,其中元件2、5、8、10所在腔室为发生冲击换热的腔室。
图7是元件1~10所在腔室的非耦合计算和耦合计算所得无量纲温度的对比。可以看出,耦合计算所得温度均高于非耦合计算所得温度。其中,腔室1、3、4、6、7、9 处主要为环腔换热,耦合换热作用较弱,耦合后温度较耦合前分别高出 0.08%、0.04%、0.19%、0.12%、0.27%、0.50%;腔室 2、5、8、10处主要为冲击换热,耦合换热作用较强,耦合后温度较耦合前分别高出 3.28%、5.13%、4.11%、10.60%。考虑耦合换热作用后,冷却空气的温度较耦合前最大差别百分比达到10.60%。耦合前后,空气系统的温升变化较大。
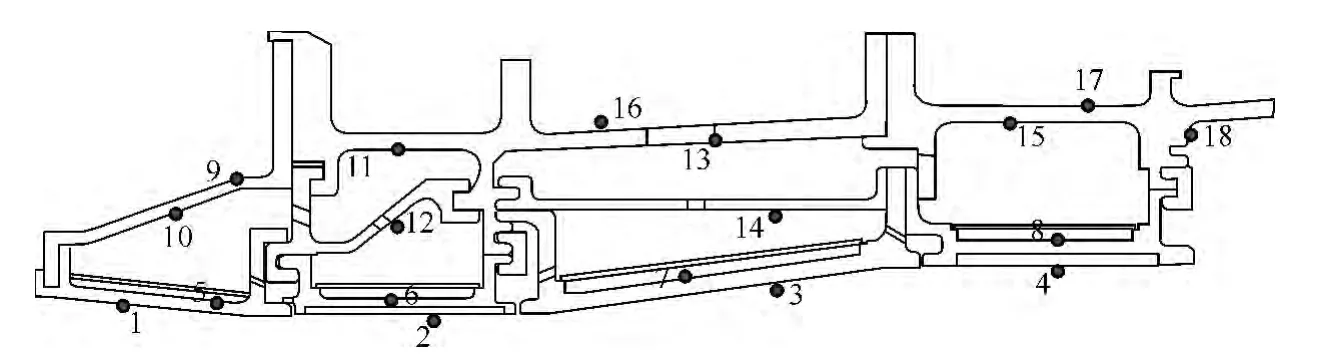
图6 高压涡轮机匣换热边界类型
图8是元件1~10所在腔室的非耦合计算和耦合计算所得无量纲压力的对比。其中,腔室1、3、4、6、7、9处,耦合后压力较耦合前分别高出0.0%、0.21%、0.50%、0.02%、0.03%、0.21%;腔室 2、5、8、10处,耦合后压力较耦合前分别高出0.21%、0.88%、0.22%、0.45%。考虑耦合换热作用后,冷却空气的压力较耦合前最大差别百分比仅为0.88%。可以看出,耦合计算所得压力值与非耦合计算压力相比,变化不明显。
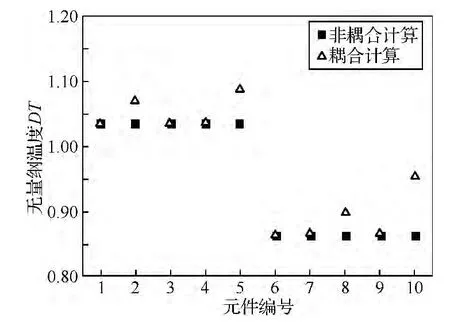
图7 耦合前后腔室无量纲温度对比
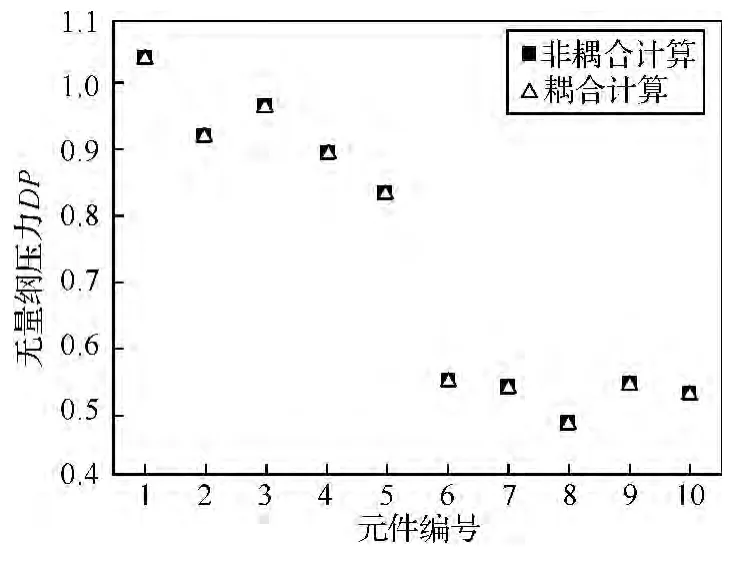
图8 耦合前后腔室无量纲压力对比
图9是元件1~10所在腔室的非耦合计算和耦合计算所得无量纲流量的对比。可以看出,耦合计算所得流量较非耦合计算均有所下降。其中,腔室1、3、4、6、7、9 处耦合后流量较耦合前分别下降0.67%、1.15%、1.15%、0.91%、0.32%、4.48%;腔室2、5、8、10处耦合后流量较耦合前分别下降0.71%、1.15%、1.64%、4.48%。4、5 腔室在同一流量分支,9、10腔室在同一流量分支,考虑耦合换热作用后,虽然冷却空气的流量较耦合前最大差别百分比达到4.48%,但是这一分支的流量值较小,对变化较为敏感。整体来说,耦合前后,空气系统的流量变化不明显。
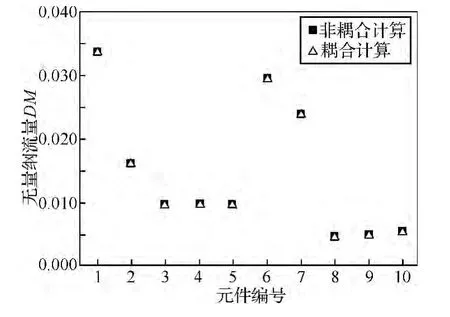
图9 耦合前后腔室无量纲流量对比
2.4 部件热分析结果
图10 和图11分别为非耦合计算和耦合计算所得高压涡轮机匣的温度场云图。对比图10和图11,耦合前后,机匣的温度场分布发生改变。耦合前,机匣最高温度在一级导叶缘板后端,无量纲温度约为1.470;最小温度在外机匣的后安装边处,无量纲温度约为0.78。耦合后,机匣最高温度所在位置不变,无量纲温度值发生改变,约为1.474,较耦合前升高了0.23%;最小温度所在位置不变,无量纲温度值发生改变,约为 0.80,较耦合前升高了1.51%。
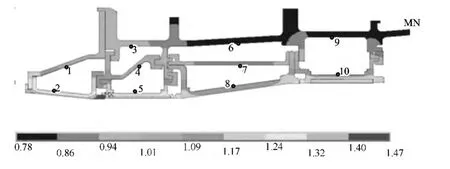
图10 非耦合计算高压涡轮机匣温度场
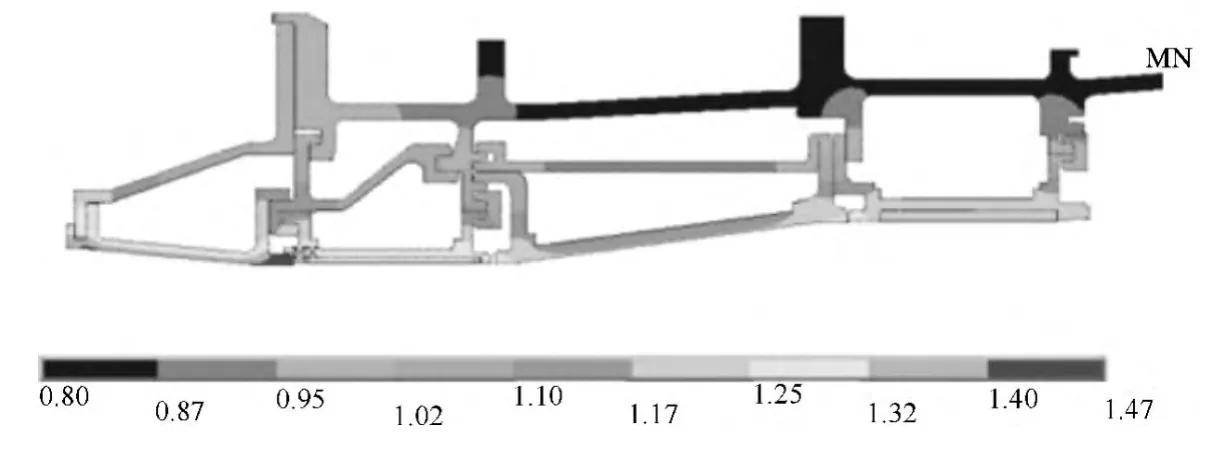
图11 耦合计算高压涡轮机匣温度场
图12为非耦合和耦合计算,高压涡轮机匣10个部位(图10所标)的固体壁面无量纲温度值的对比图。其中,壁面 1、3、4、6、7、9 处耦合后平均温度较耦合前分别高出 0.64%、0.35%、0.60%、0.36%、0.51%、1.01%;壁面 2、5、8、10 处耦合后平均温度较耦合前分别高出 2.22%、2.74%、2.17%、3.48%。耦合后,壁面平均温度值较耦合前都有所升高。特别是在耦合换热较为强烈的冲击换热壁面,考虑耦合换热作用后,温度值升高较为明显,较耦合前温度最大差别百分比达到3.48%。可见,耦合前后,热端部件的温度分布变化较为明显。
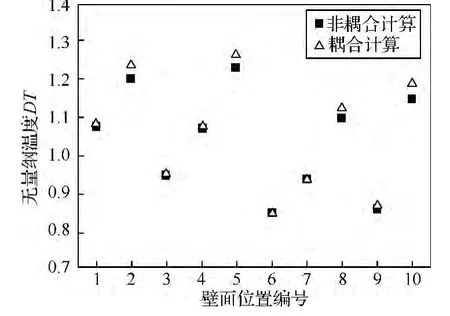
图12 耦合前后高压涡轮机匣温度对比
3 结论
本文给出了一种对航空发动机热端部件二次流动和传热耦合分析方法,二次流动采用流路网络计算方法,温度场采用有限元方法。耦合过程中传递的主要数据包括传热边界条件、零件壁温和空气系统沿程温升等参数。通过高压涡轮机匣算例的对比,结果表明耦合方法可修正沿程温升和零件温度场计算,在理论上结果更为可靠。在下一步工作中,将通过整机试验,在实际工况下对耦合计算的结果进行验证。
通过本文的方法,可提高空气系统和温度场计算的精度,并使得两者在计算中的迭代效率大大提高,特别是解决了空气系统沿程温升计算的难题,对于热端部件的空气系统和温度场计算具有重要的意义。
[1]郭文,邓化愚,刘松龄.空气冷却系统与涡轮转子温度场的耦合计算[C].中国工程热物理学会第八届年会,北京,1992.
[2]陶智,侯升平,韩树军,等.流体网络法在发动机空气冷却系统设计中的应用[J].航空动力学报,2009,24(1):1-6.
[3]Yannick Muller.Integrated Fluid Network-Thermomechanical Approach For the Coupled Analysis of a Jet Engine.ASME Paper,GT2009-59104,2009.
[4]William D.York,James H.Laylek.Three-Dimensional Conjugate Heat Transfer Simulation of an Internally-Cooled Gas Turbine Vane.ASME Paper,GT2003-38551,2003.
[5]K.Kusterer,T.Hagedorn,D.Bohn.Improvement of a Film-Cooled Blade by Application of the Conjugate Calculation Technique.ASME Journal of Turbomachinery.2006,128:572-578.
[6]John A.Verdicchio,John W.Chew,Nick J.Hills.Coupled Fluid/Solid Heat Transfer Computation for Turbine Discs.ASME Paper,GT2001-0205,2001.
[7]Tadeusz Chmielniak,Wlodzmierx Wroblewski,Grzegorz Nowak,et al.Coupled Analysis of Cooled Gas Turbine Blades.ASME Paper,GT2003-38657,2003.
[8]郭文,吉洪湖.高压涡轮导叶内冷通道流动特性计算分析[J].航空动力学报,2005,20(5):831-835.
