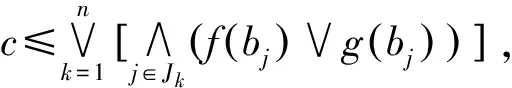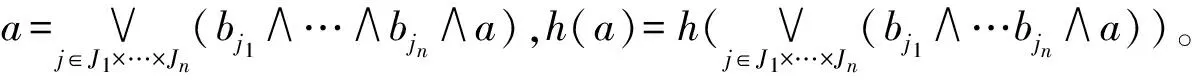伽罗瓦联络格的特性

李小光

(西安航空学院 理学院，陕西 西安 710077)

对于任意偏序集P,Q，f是P→Q的一个反序映射，如果存在一个反序g:Q→P，对于∀a∈P,x∈Q,满足g(f(a))≥a且f(g(x))≥x，则f就称为伽罗瓦联络[1]。Γ(P,Q)是P→Q的所有伽罗瓦联络形成的集合，在逐点序的条件下是偏序集合。

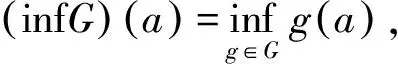
对于∀a∈P,x∈Q,令fa,gx:P→Q,且

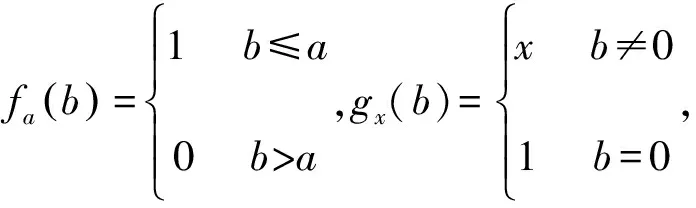
如果P,Q是非平凡的，a→fa，x→gx是分别同构于P和Q到Γ(P,Q)上的完备子格。即任何完备格P,Q，满足f:P→Q,则f是伽罗瓦联络等价于f是一个完备交联合同态，对于∀S⊆P,有f(supPS)=infQf(S)。

1 集合Γ(P,Q)的代数性质

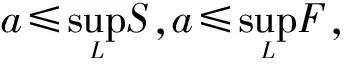
设∀a∈L是上确界，若L中的任何一个元素都是L中紧元集合的上确界，称L是代数格。

定理1 令P,Q是非平凡代数格，P具有无限交分配性，则Γ(P,Q)是一个代数格。

c=fcα(α)≤(supG)(α)=

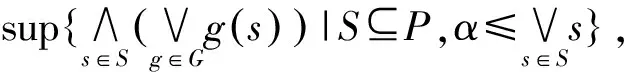
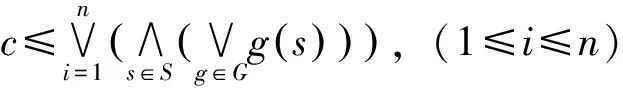
(1)

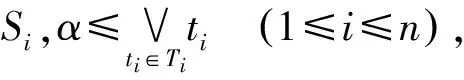
(2)

因此，α≤∨{t1∧t2∧…∧tn|t=(t1,t2,…,tn)∈T1×T2×…×Tn}

(3)

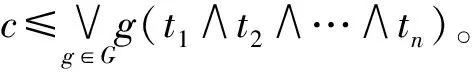
(4)

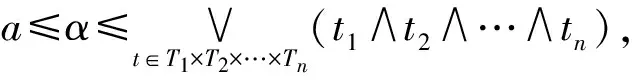
注：定理1的逆定理不成立，也就是说，P,Q不具有代数性，Γ(P,Q)也可以具有代数性。

例1 令P={0}，Q=[0,1]，在实数域R上的单位闭区间上考虑序关系，由于0

若f：P→Q，f是任一伽罗瓦联络，则f(0)=1，因此Γ(P,Q)仅有一个元素。

例2 令P={0}，Q=[0,1]，Γ(P,Q)具有代数性，即Γ(P,Q)同构于Γ(Q,P)，并且Q不具有代数性。

定理2 令P,Q是非平凡的代数格，P具有无限交的分配性，若1∈P是紧的，c∈Q，则c是紧的等价于gc⊆Γ(Q,P)是紧的，这里gc:P→Q，

证明： 因为xgx同构于Q到完备子格Q′,Q′⊆Γ(P,Q)。若Γ(P,Q)中的gc是紧的，则Q′中的gc也是紧的。因此，c∈Q也是紧的。相反地，假设c∈Q也是紧的，令G⊆Γ(P,Q)，满足。那么由于c是紧的，P中存在子集S1,S2,…,Sn，满足这里同时，由于1是紧的，存在有限子集T1,T2,…,Tn，满足Ti⊆那么，令T={t1∧t2∧…∧tn|ti∈Ti,1≤i≤n}，由于Ti,T都是有限的，因此这里t∈T。由于c是紧的，存在一个有限子集Gt⊆G,t∈T，满足令是有限的,F⊆G。令0≠a∈P,则所以这样gc是紧的。

2 Γ(P,Q)的分配性和模的性质[3-7]

设L是格，∀a,b,c∈L,a≤c,若a∨(b∧c)=(a∨b)∧c，则称L是具有模的性质(简称“是模的”)。

在代数格中任取x,y，对于任意紧元素c≤x，则x≤y等价于c≤y。

定理3[3-5]令Q是代数格，P是完备格且具有无限交分配性，则Γ(P,Q)是模的当且仅当Q是模的。

证明：设Q是模的，令f,g,h∈Γ(P,Q)，f≤h，显然f∨(g∧h)≤(f∨g)∧h。令a∈P,c∈Q是紧的，满足c≤[(f∨g)∧h](a)，则c≤(f∨g)(a)，c≤h(a)。即

(f∨(g∧h))(a)

可得c≤(f∨(g∧h))(a)，对于∀a∈P,[(f∨g)∧h](a)≤[f∨(g∨h)](a)，所以[(f∨g)∧h]≤[f∨(g∨h)]，这样Γ(P,Q)是模的。相反地，假设Γ(P,Q)是模的，由于完备子格Q在Γ(P,Q)中是嵌入的，可知Q也是模的。

定理4[6-8]令P是完备的，满足无限交分配性，Q是代数格，则Γ(P,Q)是分配的当且仅当Q是分配的。

证明：假设Q是分配格，f,g,h∈Γ(P,Q)，可知，f∨(g∧h)≤(f∨g)∧(f∨h)。

由式(2)，式(4)知

由式(1)，式(3)可得

(f∨(g∧h))(a)

≥c∧c=c。并且当a∈P时，((f∨g)∧(f∨h))(a)≤(f∨(g∧h))(a)。因此，

(f∨g)∧(f∨h)≤f∨(g∧h)，这样Γ(P,Q)是分配格。相反地，假设Γ(P,Q)是分配格，由于Q是完备子格嵌入Γ(P,Q)中，我们可知Q是分配的。

同理可得下面的定理。

定理5 令P是完备格，具有无限交分配性，Q是代数格，则Γ(P,Q)具有无限交分配性当且仅当Q具有无限交分配性。

[1] Oystein O. Galois connections [J]. Trans.Amer.Math.Soc,1994,55：493-513.

[2] Mukhopadhyay P, Ghosh S. A new class of ideal in semirings [J]. SEAMS Bull. Math,1999,23(2)：253-264.

[3] Mukhopadhyay P, Sen M K., Ghosh S. p-ideals in p-regular semirings [J]. SEAMS Bull.Math,2002,26:439-452.

[4] Ahsan J. Fully idempotent semirings[J].Proc.Japan Acad,1993,69:185-188.

[5] Birkhoff G. Lattice Theory [M]. Publication: Amer.Math.Soc.Colloq,1954.

[6] Borzooei R A, Zahedi M M.(Anti) fuzzy positive implicative hyper k-ideals[J].Italian J. Pure and Appl.Math,2003,14:9-22.

[7] 王国俊. 非经典数理逻辑与近似推理[M].北京:科学出版社,2000.

[8] 姚炳学.群和环上的模糊理论[M].北京:科学出版社,2007:84-88.