基于线性二次型最优控制器的平行双倒立摆系统稳定控制

戚东东 张春 张传松 谭子良

（安徽工程大学 电气工程学院，安徽芜湖 241000）

基于线性二次型最优控制器的平行双倒立摆系统稳定控制

戚东东 张春*张传松 谭子良

（安徽工程大学 电气工程学院，安徽芜湖 241000）

倒立摆控制系统是一个典型的高阶次、不稳定、多变量、非线性和强耦合控制系统。本文在建立平行双倒立摆控制系统数学模型的基础上，设计了线性二次型最优调节器（LQR）以实现对平行双倒立摆系统的最优控制，并通过MATLAB仿真实验验证了该方法的有效性。

倒立摆；建模；LQR控制；仿真

倒立摆系统的控制是控制理论应用的一个典型范例，其结构简单、成本较低，便于用模拟或数字方法进行控制。虽然其结构形式多种多样，但无论何种结构，就其本身而言，都是一个非最小相位、多变量、绝对不稳定的非线性系统［1］。由于倒立摆系统的绝对不稳定性，必须采取有效的措施进行稳定。其控制方法在军工、航天、机器人领域和一般工业过程中都有着广泛的用途，因此很多学者提出很多的控制方法［2-6］，然而这些控制方法主要应用在单摆系统中，而对平行双倒立摆系统的控制研究则较少，文献［7］应用滑模变结构的控制方法对双摆系统进行了控制研究，文献［8］应用拟人智能控制方法对两摆间有弹簧连接的平行单级双倒立摆的稳定控制和两个电机的解耦控制问题进行了研究，文献［9］应用线性理论的控制方法对两摆杆长度相同的平行双倒立摆系统进行了控制研究。

本文分析了平行双倒立摆系统的特定物理结构并进行合理建模，探讨使用线性二次型最优调节器（linear ruadraticregulator，LQR）实现对两摆杆长度不同的平行双倒立摆系统的稳定控制问题。

1 平行一级双倒立摆的数学模型

1.1 数学模型的建立［4］

为简化系统分析，在模型建立过程中，忽略空气流动阻力以及各种次要的摩擦力。这样，可将双倒立摆系统抽象成小车和两个匀质刚性杆组成的系统（如图1所示），其中，M为小车的质量；x为小车水平方向的位移；F为加在小车上的力；m1、m2分别为左右两个摆杆的质量；2L1、2L2分别为左右两个摆杆的长度；J1、J2分别为左右两个摆杆的转动惯量；θ1、θ2分别为左右两个摆杆与竖直方向上的夹角，即摆角。

对小车和摆杆分别进行受力分析，运用牛顿第二定律得双倒立摆系统的精确数学模型为

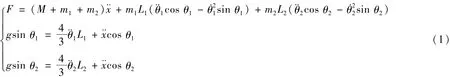
图1 平行一级双倒立摆系统

1.2 数学模型的线性化

在两摆摆角|θ1|，|θ2|＜10度时，设cosθ1≈1，cosθ2≈1，sinθ1≈θ1，sinθ2≈θ2，则线性化处理后的微分方程组为

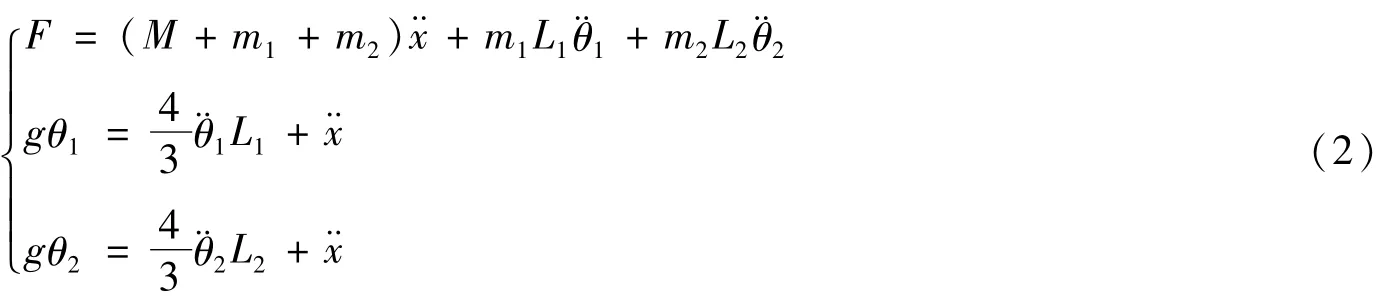
设状态变量为x、˙x、θ1、˙θ1、θ2、˙θ2，经过变换易得状态空间表达式为

其中q=4M+m1+m2。

2 LQR控制器设计

2.1 系统能控性分析

系统能控性是LQR控制器设计的前提，通过编程求解系统能控性矩阵N=［B AB A2B A3B A4B A5B］的秩，大量仿真实验表明只要L1≠L2，系统能控矩阵N的秩f=6，系统状态完全能控；而当L1=L2时，f=4＜6，系统状态不完全能控。

2.2 LQR控制器设计

线性二次型（Linear Quadratic，LQ）是指系统的状态方程是线性的，指标函数是状态变量和控制变量的二次型。线性二次型控制理论已成为反馈系统设计的一种重要工具，它为多变量反馈系统的设计提供了一种有效的分析方法，它适应于时变系统，可以处理扰动信号和测量噪声问题以及处理有限和无限的时间区间等问题。

考虑系统的状态方程为

设状态反馈控制律u（t）=-Kx（t），使得二次型性能指标最小

其中，x（t）为系统的状态变量；tf、t0为终止时间与起始时间；S为终态约束矩阵；Q（t）为运动约束矩阵；R（t）为约束控制矩阵。其中Q（t）、R（t）决定了系统误差与控制能量消耗之间的相对重要性。为使J最小，由最小值原理得到最优控制为

式中，矩阵P（t）为微分Riccatti方程-P（t）A-ATP（t）+P（t）BR-1BTP（t）-Q的解。如果令终止时间tf=∞，P（t）为一个常数矩阵，且P（t）=0，则以上Riccatti方程简化为

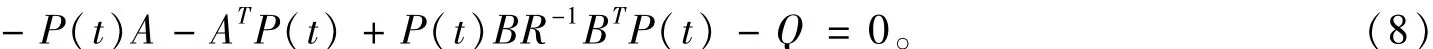
因此可求得J取极小值时的最优反馈系数矩阵为

对于最优反馈系数矩阵K，可使用MATLAB中专门的求解工具lr r（A，B，Q，R）来求取。将LQR控制方法用于倒立摆控制的原理如图2所示。

图2 LQR倒立摆控制算法原理图

lr r函数允许选择两个参数R和Q，这两个参数用来平衡输入量和状态量的权重。假定R=0.1，Q= C’*C，Q矩阵为6阶方阵，其中对角线上Q1，1代表小车位置权重，而Q3，3，Q5，5是摆杆角度的权重。

2.3 仿真与分析

设双倒立摆控制系统参数为：M=2 Kg，m1=m2=0.3 Kg，2L1=0.7m，2L2=0.6m，g=9.8 m/s2，F=0.3（阶跃信号）。

取Q1，1=1，Q3，3=1，Q5，5=1时，可得K=［3.16 7.70 1 937.64 598.65 -1 871..36 -534.04］，此时系统的响应曲线如图3所示。

从图3中可以看出，当状态变量的权重取得较小时，摆角响应的超调量很小，但稳定时间和上升时间偏大，小车向正方向移动时，摆角经短暂时间回复稳定位置。

若取Q1，1=10 000，Q3，3=100，Q5，5=100，则得K=［316.23 413.37 22 305.24 6 884.22 -19 683.04 -5 623.09］，此时系统响应曲线如图4所示。

从图4可知，通过适当增大Q矩阵中的Q1，1和Q3，3与Q5，5，系统的稳定时间和上升时间变短，摆角超调量和摆杆的角度变化也同时减小。当Q1，1、Q3，3、Q5，5及R取最优值时即可实现对系统稳定的最优控制。

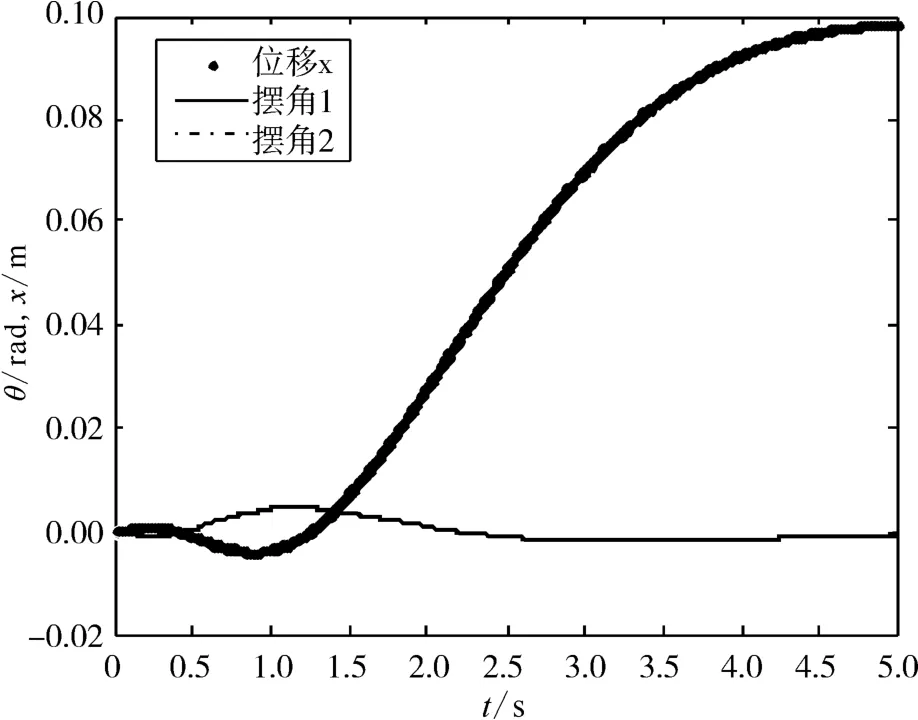
图3 系统阶跃响应曲线（摆角1和2重合）

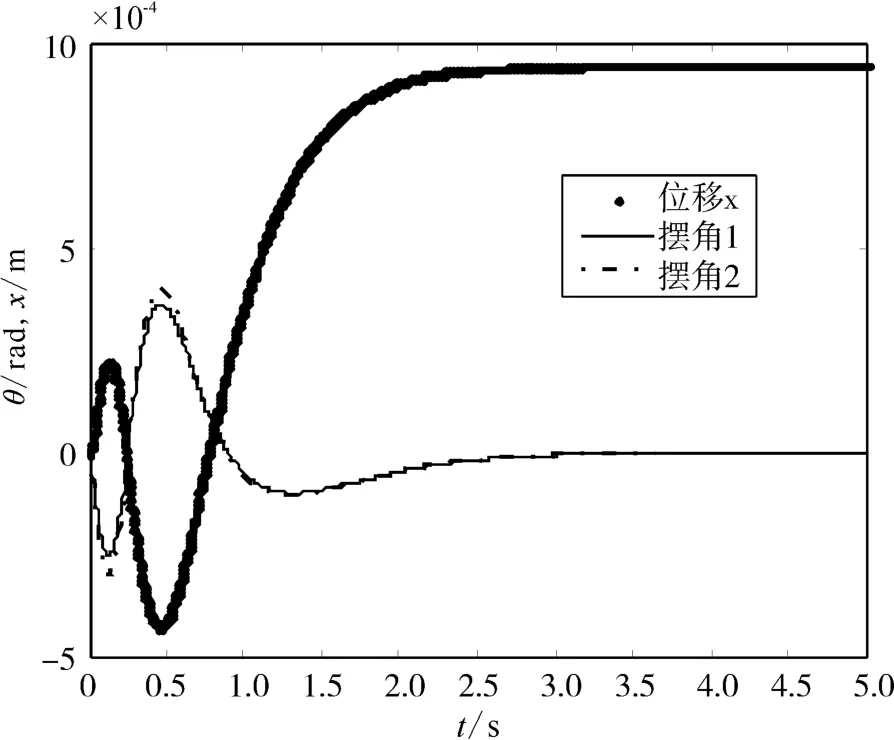
图4 系统阶跃响应曲线

3 结语

利用牛顿定律建立了平行一级双倒立摆系统的数学模型，分析了系统的能控性，采用LQR控制原理设计了控制器，并采用MATLAB软件对控制器的控制性能进行了仿真研究，实验验证了控制器设计的合理性，仿真结果表明设计的LQR控制器对平行双倒立摆系统进行了有效的稳定控制，且该控制方法设计简单，容易实现。

［1］ 裴月琳.倒立摆系统稳摆控制算法研究［D］.重庆：重庆大学，2012.

［2］ 孙灵芳，孔辉，刘长国，等.倒立摆系统及研究现状［J］.机床与液压，2008，36（7）：306-310.

［3］ 付莹，张广立，杨汝清.倒立摆系统的非线性稳定控制及起摆问题的研究［J］.组合机床与自动化加工技术，2013（1）：35-37.

［4］ 王国政，李虹，董宗慧.平面一级倒立摆的稳定控制［J］.工业控制计算机，2013，26（3）：36-39.

［5］ 邱德慧，王庆林，杨洁.倒立摆系统的动力学建模与滑模控制［J］.控制工程，2012，19（90）：8-14.

［6］ 刘凯.一级倒立摆系统设计与LQR最优控制仿真［J］.工业仪表与自动化装置，2012（3）：10-13.

［7］ 张春，徐开红，江明.基于滑模的平行双倒立摆系统稳定控制研究［J］.昆明理工大学学报，2008，33（3）：78-81.

［8］ 李诚，张明廉，张志新.拟人控制平行单级双倒立摆［J］.航空学报，2006，27（1）：115-119.

［9］ 刘金亨，陈今润，吕郁青，等.基于LQR的一阶直线双倒立摆最优控制系统研究［J］.自动化技术与应用，2009，28（5）：11-13.

Stabilization Control of Parallel Type Inverted PendulumBasedon Linear Quadratic Optimal Controller

QIDong-dong ZHANG Chun*ZHANG Chuan-song TAN Zi-liang

（Electrical Engineering College，Anhui Polytechnic University，Wuhu 241000，China）

Inverted pendulum control system is a typical high order，unstable，multivariable，nonlinear and strong coupling control system.Based on building the mathematical model of the parallel double inverted pendulum control system，the linear ruadraticregulator（LQR for short）is designed to achieve optimal control of the parallel double inverted pendulum system.Simulation experiments show that the method is effective.

inverted pendulum；modeling；LQR control；simulation

TP273

A

1009-0312（2014）03-0008-04

2013-12-18

安徽省自然科学基金项目（1208085MF115）；国家级大学生创新创业训练计划项目（201210363040）。*通讯作者：张春（1972—），男，安徽望江人，副教授，硕士，主要从事电气传动、智能控制等方面的教学与研究。