一类非线性系统的状态反馈输出跟踪研究

朱泓霖，王兴平

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

一类非线性系统的状态反馈输出跟踪研究

朱泓霖a，王兴平b

（海军航空工程学院a.研究生管理大队；b.基础部，山东烟台264001）

研究一类非线性系统的状态反馈输出跟踪控制问题。对于给定的光滑有界的参考信号，利用反步方法设计系统的跟踪控制器，使从任意初值出发的系统的输出都渐近于给定的参考信号，同时系统内部状态保持有界。仿真实例验证了研究结论的可行性。

非线性系统；输出跟踪；状态反馈；反步方法

通过反馈控制器使得受控系统的输出渐近逼近给定的参考信号是控制工程中一个重要问题。这类问题在航天器的轨迹控制[1-2]、船舶航行控制[3-5]、水下机器人控制[6]等诸多领域有着广泛地应用，一直是控制理论研究的重点。

近年来，线性系统的输出跟踪问题得到了充分研究，并取得了系统的成果[7]。随着非线性系统控制理论的发展，非线性系统的输出跟踪控制问题研究也产生了一系列的学术研究成果。文献[8]利用非线性系统的几何理论研究了一类具有最小相位非线性系统的跟踪问题。文献[9]讨论了一类下三角形式非线性系统的全局输出反馈跟踪问题，通过提出一种新的动态增益缩放技术给出了输出反馈控制器的设计方法。文献[10]讨论了一类不满足线性增长条件的不确定非线性系统的输出反馈跟踪问题，并基于变结构观测器用反步方法，设计了输出反馈控制器。同时，实用跟踪控制问题备受关注，它要求设计控制器使得系统输出与给定参考信号的渐近误差小于给定的数，文献[11-12]研究了非线性系统的输出反馈实用跟踪问题。

1 问题描述

本文研究一类下三角结构非线性系统的状态反馈输出跟踪控制问题。与文献中的方法不同的是，根据系统的结构特点，本文构造了在系统输出跟踪参考信号时系统状态的渐近轨迹，由此将系统的跟踪问题变成一个系统向渐近轨迹的镇定问题，并采用反步设计方法设计出输出跟踪控制器，使得这一方法的实现较为简单。

考虑如下形式的非线性系统：

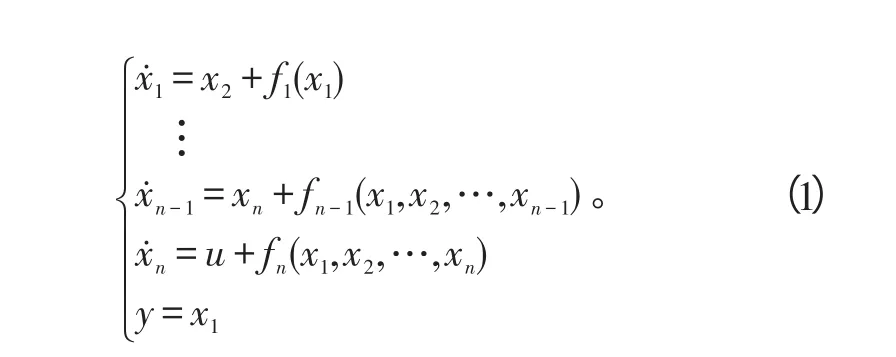
式（1）中：xi∈ℝ(i=1,2,…,n)是系统状态；u∈ℝ是控制输入；y=x1是系统输出；fi(i=1,2,…,n)均是光滑函数。

本文研究的问题为：对给定的有界参考信号yr(t),t≥0，其各阶导数也有界，设计如下形式的状态反馈输出跟踪控制器：

使得从任意初值出发的闭环系统（1）、（2）的输出y(t)满足lti→m∞(y(t)-yr(t))=0，同时系统内部状态是有界的。

2 跟踪控制器的设计

对给定的参考信号yr(t)，若系统（1）在某一控制下从某一初值出发的系统输出恰好是x1(t)≡yr(t)，由系统方程，则能够推出系统的内部状态为：

如系统输出y=x1是渐近趋于参考信号p1(t)的，则对于系统状态xi(t)应有xi(t)-pi(t)→0(t→∞)。即能够实现输出跟踪的跟踪控制器也可以实现xi(t)-pi(t)→0。反之，实现xi(t)-pi(t)→0的控制器也是实现输出跟踪的跟踪控制器。基于这一分析，可以把输出跟踪控制问题与一个关于xi(t)-pi(t)的镇定问题联系一起。

首先，建立关于xi-pi的动态方程，令对1≤i〈n，计算

对i=n，计算

得到关于xi-pi的动态方程

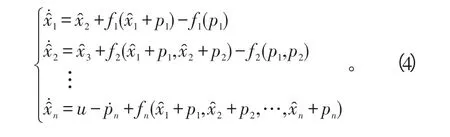
可以把系统写成简单形式：

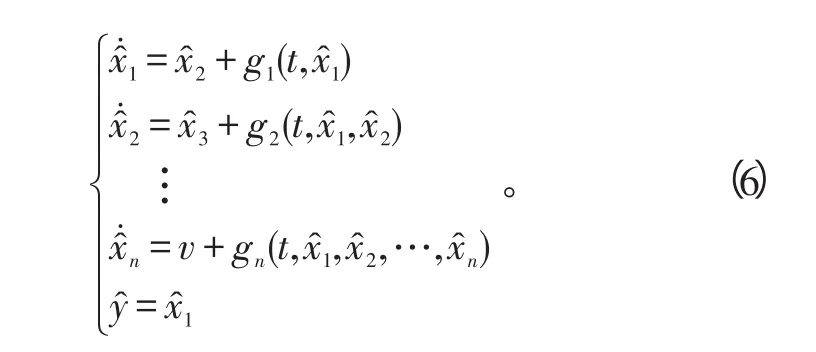
系统（1）的输出对参考信号的跟踪问题就变成系统（6）的镇定问题。

然后，利用反步方法设计系统的控制器v实现系统的镇定。

反步设计方法是针对非线性系统的一种系统化的控制器设计方法，它将Lyapunov函数的构造与控制器的设计结合一起，解决了以往非线性系统稳定性中Lyapunov函数的存在性问题。它通过从系统的最低阶次微分方程开始，引入虚拟输入的概念，一步步构造Lyapunov函数并进行虚拟输入的设计，最终设计出真正的控制律。

反步设计方法是一种递归设计方法，具有系统化、程序化的特点。

下面用反步设计方法，递归构造实现系统（6）镇定的状态反馈控制器v。

第1步：构造Lyapunov函数

对其求导得

选取虚拟输入u1，则

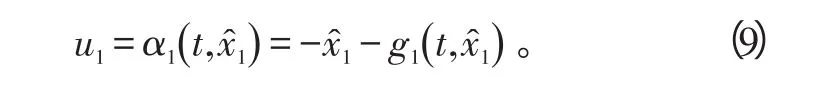
当x^2取做虚拟控制u1时，可以使得式（8）是负定的，从而实现了对x^1的控制。

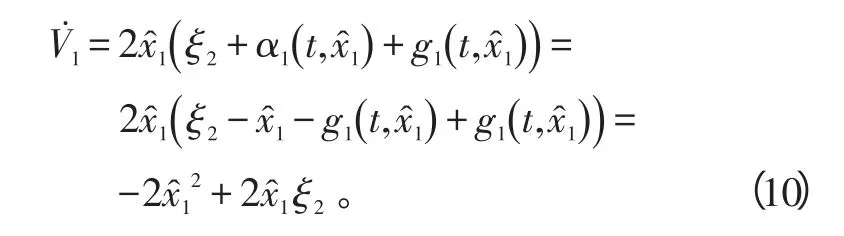
第k步：考虑系统

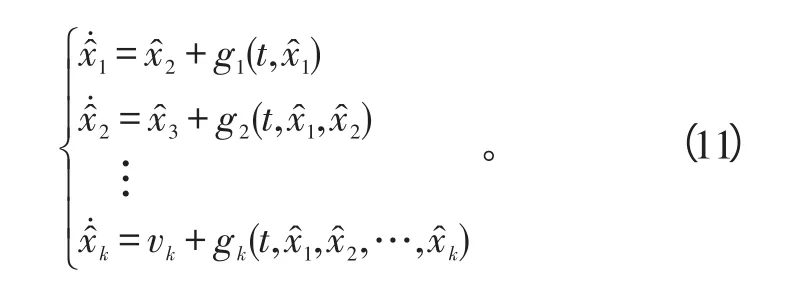
假设存在光滑函数

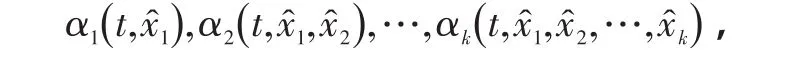
满足

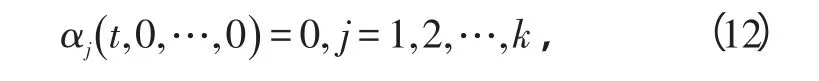
并且，

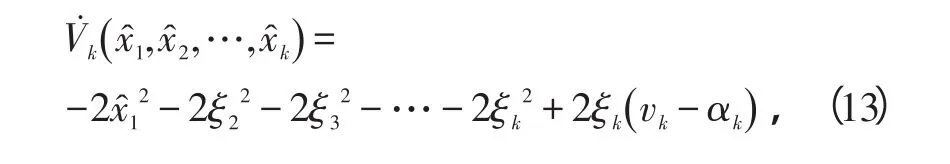
式中，

第k+1步：现在考虑系统

构造Lyapunov函数

计算Vk+1的导数V˙k+1，由归纳步骤假设得

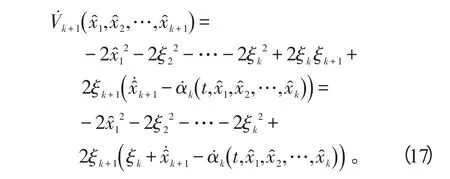
根据链法则可以得到

再由式（12）可以得到

又因为全部gi在原点的值是0，并且利用式（18）得到

于是式（17）可以整理成如下形式：

根据αk+1的表达式，并考虑它是光滑的，根据式（14）、（19）可以得到αk+1() t,0,…,0=0。

按照归纳步骤进行到n步时，可以得到控制器

将上面推导叙述成如下结论。

定理：对于非线性系统

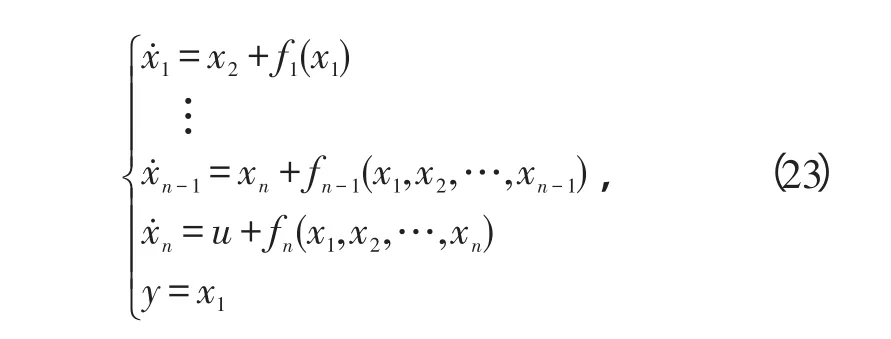
可经递归步骤设计反馈输出跟踪控制器

可以使得闭环系统（23）、（24）的输出y(t)都渐近趋于给定的参考信号yr(t)，即

3 仿真及实例

考虑一个二阶系统

可由反步方法确定计算出：

图1 系统输出y(t)对参考信号yr(t)的跟踪Fig.1 Tracking of system out put signal y(t) to the reference signal yr(t)

4 结语

本文研究一类非线性系统的状态反馈输出跟踪控制问题。首先，建立了系统状态在实现输出跟踪时的渐近轨迹，进而建立了可以描述系统状态和渐近轨迹偏差的动态方程，最终将输出跟踪问题转化为对偏差系统的镇定问题；其次，利用递归的反步设计方法给出了偏差系统的镇定控制器，这一控制器解决了系统的状态反馈输出跟踪控制问题；最后，给出了一个仿真实例，仿真结果表明设计的跟踪控制器是可行的。

[1] NO T S，MIN B M，STONE R H，et al.Control and simulation of arbitrary flight trajectory-tracking[J].Control Engineering Practice，2005，13（5）：601-612.

[2] SHARMA R，TEWARI A.Optimal nonlinear tracking of spacecraft attitude maneuvers[J].IEEE Transactions on Control Systems Technology，2004，12（5）：677-682.

[3] KIMS H，YAMATO H.On the design of a longitudinal motion control system of a fully-submerged hydrofoil craft based on the optimal preview servo system[J]. Ocean Engineering，2004，31（13）：1637-1653.

[4] CIMEN T，BANKS S P.Nonlinear optimal tracking control with application to super-tankers for autopilot design [J].Automatica，2004，40（10）：1845-1863.

[5] DO K D，PAN J.State and output-feedback robust path follow ing controllers for underactuated ships using Serret Frenet frame[J].Ocean Engineering，2004，31（5-6）：587-613.

[6] KIMK，URA T.Fuel-optimally guidance navigation and tracking control of AUV under current interaction[C]// IEEE Oceans Conference Record.2003：663-670.

[7] 郑大钟.线性系统理论[M].2版.北京：清华大学出版社，2002：305-310. ZHENG DAZHONG.Linear system theory[M].2nd ed. Beijing：Tsinghua University Press，2002：305-310.（in Chinese）

[8] ISIDORI A.Nonlinear control systems[M].3rd ed.London：Springer-Verlag，1995：190-202.

[9] ZHANG X，LIN Y.A new approach to global asymptotic tracking for a class of low-triangular nonlinear systems via output feedback[J].IEEE Transactions on Automatic Control，2012，57（12）：3192-3196.

[10] ZHANG K J，FENG C B，FEI S M.Robust output feedback tracking for a class of uncertain nonlinear systems [J].Control Theory&Applications，2003，20（2）：173-179.

[11] GONG Q，QIAN C.Global practical tracking of a class of nonlinear systems by output feedback[J].Automatica，2007，43（1）：184-189.

[12] ANDRIEU V，PRALY L，ASTOLFI A.Asymptotic tracking of a reference trajectory by output feedback for a class of nonlinear systems[J].Systems&Control Letters，2009，58（9）：652-663.b.Department of Basic Sciences,Yantai Shandong 264001,China）

Research on State Feedback Tracking of the Nonlinear Systems

ZHU Hong-lina,WANG Xing-pingb
（Naval Aeronautical and Astronautical University a.Graduate students'Brigade;

The problem of state feedback tracking control of a class of nonlinear systems was studied.For a given bounded smooth reference signal,the tracking controller was presented by backstepping method.The controller made the outputs of the controlled systems asymptotically approach the given signal and all internal states keep bounded.Finally,a numeric simulation illustrated the effectiveness of the method.

nonlinear system;output tracking;state feedback;backstepping approach

TP273.4

A

1673-1522（2014）04-0311-04

10.7682/j.issn.1673-1522.2014.04.003

2014-03-28；

2014-04-23

朱泓霖（1989-），男，硕士生。