步进调频SAR子带误差估计新方法

吴明宇， 杨桃丽， 吴顺君， 李真芳

(西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071)

合成孔径雷达系统通过发射线性调频信号获得距离高分辨图像，随着分辨率要求的提高，发射信号的带宽也随之提高，例如 0.1 m 分辨率要求发射信号带宽达到 1.8 GHz 以上．发射如此大带宽的信号面临着很多技术和方法上的难题，常用的解决方案为发射若干个不同载频的子带信号，然后通过数字信号处理的方法将各个子带信号进行合成，从而得到宽带信号，获得距离高分辨图像[1-5]，即利用步进频线性调频信号合成大带宽信号．理想情况下，各子带信号除中心频率不同外，其余完全相同，此时可以采用典型的子带拼接法[6-7]得到全频带图像．但在实际情况中，由于系统硬件等不可避免地存在各种误差，导致各子带信号的不一致，从而影响合成信号的质量[7-10]．因此必须对各子带信号误差进行估计并补偿．文献[7]提出通过测量外部真实强点目标(例如角反射器)来构造校正压缩滤波器，当场景中不存在强目标时该方法可能会失效．文献[8]提出一种利用内定标数据进行误差估计校正的方法，该方法首先对各子带的内定标数据分别进行成像处理，然后比较各子带的成像结果得到子带误差，当不存在内定标数据则无法利用此方法进行误差估计．

考虑到实际情况，各子带信号间通常要设置一定的重叠度，重叠量一般为5%～10%，在这种情况下，回波信号无论是在时域还是在频域都表现为子带间有交叠．基于此，笔者利用各子带信号间的重叠部分，提出了一种基于回波数据的子带误差估计校正方法，同时通过对各子带回波进行加窗以消除因子带重叠而引起的成对回波．

1 信号模型

如图1所示的几何坐标系，X轴为载机速度方向，Z轴背向地面，Y轴由右手坐标系确定．雷达按顺序发射接收各子带信号，如图2所示，图中k表示子带编号 (k=1，2，…，K，K为总子带个数)，这里以K=4 为例，在某一脉冲时刻发射接收子带1，在下一脉冲时刻发射接收子带2，……，依次类推，一直到第4个脉冲时刻发射接收完子带4，然后在第5个脉冲时刻重复发射接收子带1．

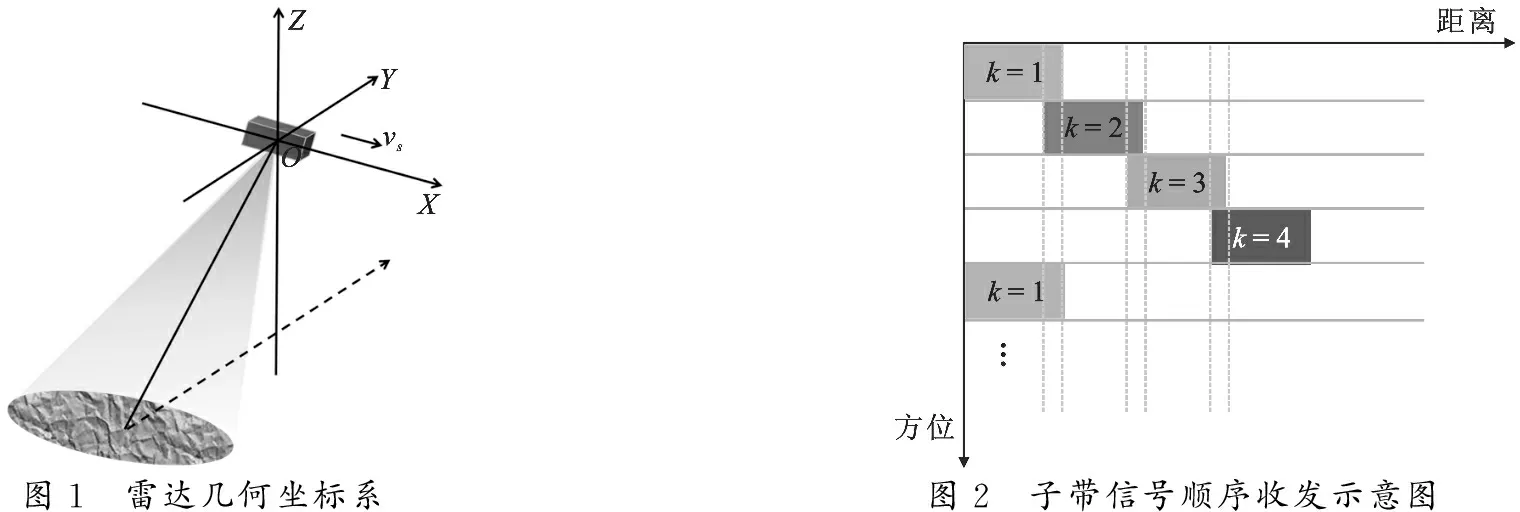
图1 雷达几何坐标系图2 子带信号顺序收发示意图

假设各子带带宽为Brn，脉冲持续时间为Tpn，调频率为γ，第k个子带的发射信号为

(1)

假设雷达的起始坐标为(0，0，0)，时刻t时为(vst，0，0)(vs为载机速度)，且在时刻t时接收的解调后的第1个子带回波信号为

(2)

其中，t代表方位慢时间，c是光速，r1(t)为地面单元(x，y，z)到雷达的瞬时斜距，σ(x，y，z)表示地面单元(x，y，z)处的复反射系数，g(t)表示天线方向图，

r1(t)=((x-vst)2+y2+z2)1/2．

(3)

同样地，再经过k-1个脉冲后，接收到第k个子带的回波信号为

其中，fp为脉冲重复频率．由于不同子带的回波信号在方位向各有差异，不能直接作子带合成．观察式(3)和式(5)可知，只需将各子带信号在方位向对齐即可，具体实现时可将各子带回波信号变换到多普勒频域，然后再乘以一个线性相位即可．将各子带回波在方位向上对齐后，各子带回波即可等效为同一脉冲时刻的接收回波．这样，通过子带合成方法[6-7]即可得到高分辨SAR图像．然而，由于系统硬件等原因，各子带间不可避免地存在一定的误差，将会严重影响子带合成的性能．

根据实际系统情况，笔者主要考虑子带间存在的幅相误差和延时误差[8]．当存在子带误差时，假设各子带信号已相对第1个子带回波进行了延时，回波信号变为

其中，Δτk、Δφk和Ak分别表示第k个子带相对第1个子带的延时误差、相位误差和幅度误差，n(τ，t)为高斯白噪声．

2 子带误差估计

考虑实际系统中滤波器的特性，各子带信号间通常会设定一定的重叠度[11]，如图2所示．当各子带间存在一定重叠谱时，若直接对各子带回波进行相干叠加则会导致信号幅度有凸起，这种重叠谱的非平坦性将导致聚焦结果中成对回波的出现．笔者将结合子带误差校正同时消除重叠谱中的波纹．理想情况下，相邻子带间的重叠谱在相位上应是相同的，但由于系统误差等因素的影响，使之发生了变化，笔者正是基于此进行子带误差估计的．

首先对各子带回波进行距离向插值升采样处理，插值倍数由子带个数决定[6]，使之满足全带宽奈奎斯特(Nyquist)采样，然后对式(6)进行距离快速傅里叶变换(FFT)到距离频域，忽略常数值，得

其中，fτ表示距离频域．对式(7)乘以距离匹配函数，得

进行频移，得

此时，各子带的频谱分布如图3所示，图中以2个子带为例，提取相邻子带间的重叠谱部分，如图3两条虚线的中间部分所示，然后再将其相除，得

(10)

图3 频移后的各子带频谱

因式(10)为对相邻子带间的重叠谱部分进行操作，故在此处省略了rect(fτ)项．需要说明的是，利用式(10)获取的为一随距离频率的变化值，而并非单一数值．

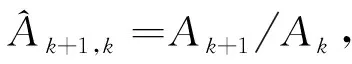
重复以上操作即可得到所有相邻子带间的幅相误差和延时误差．以第1个子带为参考，估计得到的子带k的幅相误差和延时误差为

图4 子带重叠谱加窗示意图

为提高估计精度，可利用多个方位脉冲进行平均以消除噪声的影响．利用式(13)～(15)得到的子带误差对各子带回波进行误差补偿，然后再对各子带间重叠谱部分进行加窗处理，以消除因重叠谱引起的成对回波，如图4所示，图中以K=4 为例．各子带的窗函数为

(16)

其中,

其中，fk=(k-(K+1)/2)fstep，为各子带频移后的中心频率，fover=Brn-fstep，为相邻子带间的重叠频谱．最后将各子带回波进行相干叠加，即可得到全带宽数据，再进行传统SAR成像处理，得到高分辨SAR图像．

3 实验验证

下面利用仿真数据和地基实测数据对文中方法进行验证，由于笔者已知的现有子带误差估计方法大多都基于一定的先验条件[7-8]，如定标数据等，故在此处无法将文中所述方法与其他方法进行对比，仅给出了利用文中方法所得到的处理结果．

表1 仿真参数

3.1 仿真数据验证

仿真参数如表1所示，其中，Rc表示场景中心斜距，相邻子带的重叠频谱为 8 MHz．

图5(a)给出了距离和方位均距场景中心1 km的点目标成像后的距离剖面图，图中实线为单子带成像结果，点划线为子带合成但未对相邻子带重叠谱进行处理的结果，虚线为子带合成并利用上述加窗方法对相邻子带重叠谱进行处理后结果，从图中可以看出，文中方法很好地对因子带重叠引起的成对回波进行了抑制．图5(b)给出了当各子带间存在幅度误差[1，1.2，0.9，1.3]，相位误差[0°，-10°，50°，30°]及延时误差 [0 ns，5 ns，-4 ns，2 ns] 时的处理结果，图中实线为无误差的处理结果，点划线为未进行误差补偿直接子带合成的结果，虚线为采用文中方法进行误差估计补偿后的子带合成结果，从图中可以看出，文中方法很好地实现了子带误差估计．

图5 仿真数据处理结果

图6给出了误差估计精度随信噪比(Signal to Noise Ratio， SNR)的变化，纵坐标为估计值的平均均方根误差(Averaged Root-Mean-Square Error， ARMSE)，这里假设噪声为高斯白噪声．在实验中，对每个信噪比均进行了100次重复实验，并利用20个方位脉冲进行平均以减小噪声的影响．可以看出，该方法很好地实现了子带误差估计．

图6 误差估计精度随SNR的变化

3.2 实测数据验证

下面给出利用某研究所获取的陕西华山山脉的地基子带数据进行处理的结果，系统基本参数如表2所示．

表2 实测数据参数

图7给出了子带重叠为 6.5 MHz 时的处理结果，图7(a)为单子带成像结果，图7(b)为误差校正前的成像结果，图7(c)为利用文中重叠谱估计法进行误差校正后的成像结果，其中右侧图为左侧图小方框内图像的局部放大图．从图中可以看出，图7(a)的亮度明显低于图7(b)的亮度，即单子带成像结果的分辨率低于子带合成后的，这可通过图像的对比度看出．在进行子带误差校正前，图像出现了一定程度上的散焦现象，如 图7(b) 右侧的放大图所示．而子带误差校正后图像的清晰度得以提高，图像细节更加明显，如图7(c)右侧的放大图所示，从而说明该方法很好地实现了误差校正．

图7 子带重叠为6.5 MHz时的处理结果

4 结 束 语

通过发射若干中心频率以一定步长提高的调频子带信号，然后进行带宽合成获得大带宽信号，可以减轻直接发射大带宽信号带来的技术和方法问题．但是，由于系统硬件等因素的影响，各子带信号间不可避免地存在一定的误差，从而影响子带合成的质量．笔者利用子带间的重叠频谱，提出了一种子带误差估计方法，同时通过对各子带回波进行加窗处理以消除因子带重叠而引起的成对回波．计算机仿真数据和地基实测数据验证了该方法的有效性．

[1] Wehner D R. High-resolution radar [M]. 2nd ed. Norwood: Artech House, 1995.

[2] 王岩飞, 刘畅, 李和平, 等. 基于多通道合成的优于0.1 m分辨率的机载SAR系统 [J]. 电子与信息学报, 2013, 35(1): 29-35.

Wang Yanfei, Liu Chang, Li Heping, et al. An Airborne SAR with 0.1 m Resolution Using Multi-channel Synthetic Bandwidth [J]. Journal of Electronics & Information Technology, 2013, 35(1): 29-35.

[3] 刘峥, 刘宏伟, 张守宏. 步进频率信号分析 [J]. 西安电子科技大学学报, 1999, 26(1): 71-74.

Liu Zheng, Liu Hongwei, Zhang Shouhong. Analysis of the Step Frequency Signal [J]. Journal of Xidian University, 1999, 26(1): 71-74.

[4] 刘亚波, 李军, 李亚超, 等. 解线频调步进频率ISAR成像研究 [J]. 西安电子科技大学学报, 2010, 37(3): 469-475.

Liu Yabo, Li Jun, Li Yachao, et al. Study on Dechirp SF ISAR Imaging [J]. Journal of Xidian University, 2010, 37(3): 469-475.

[5] 程普, 王展, 方凌江, 等. 调频连续波SAR方位多波束成像 [J]. 现代电子技术, 2013, 36(3): 12-20.

Cheng Pu, Wang Zhan, Fang Lingjiang, et al. Imaging of FMCW SAR Using Multiple Azimuth Beams [J]. Modern Electronics Technique, 2013, 36(3): 12-20.

[6] Lord R T, Inggs M R. High Resolution SAR Processing Using Stepped-frequencies [C]//International Geoscience and Remote Sensing Symposium: 1. Piscataway: IEEE, 1997: 490-492.

[7] Wilkinson A J, Lord R T, Inggs M R. Stepped-frequency Processing by Reconstruction of Target Reflectivity Spectrum [C]//Proceedings of the 1998 South African Symposium on Communications and Signal Processing. New York: IEEE, 1998: 101-104.

[8] Deng Y, Zheng H, Wang R, et al. Internal Calibration for Stepped-frequency Chirp SAR Imaging [J]. IEEE Geoscience and Remote Sensing Letters, 2011, 8(6): 1105-1109.

[9] 郜参观, 邓云凯, 冯锦. 通道失配对多通道子带合成SAR性能的影响分析与补偿[J]. 电子与信息学报, 2012, 34(1): 154-159.

Gao Canguan, Deng Yunkai, Feng Jin. Influences of Mismatch on the Multi-channel Synthetic-bandwidth SAR System and the Corresponding Correction Measure [J]. Journal of Electronics & Information Technology, 2012, 34(1): 154-159.

[10] 孙林, 田卫明, 曾涛. 调频步进频雷达中距离起点误差分析 [J]. 电子与信息学报, 2012, 34(5): 1070-1075.

Sun Lin, Tian Weiming, Zeng Tao. Error Analysis of Beginning Sampling Range in Stepped Chirp Radars [J]. Journal of Electronics & Information Technology, 2012, 34(5): 1070-1075.

[11] Brenner A R, Ender J H G. First Experimental Results Achieved with the New Very Wideband SAR System PAMIR [C]//Porceedings of 4th European Conference on Synthetic Aperture Radar. Berlin: VDE Verlag GMBH, 2002: 81-86.