动态Job Shop调度仿真中的交货期设置问题研究

范华丽，熊禾根，钱国洁，蒋国璋，李公法

（武汉科技大学 机械自动化学院，武汉 430081）

0 引言

调度问题自被提出以来，一直受到各个学科和领域的广泛关注。调度问题有多种类型，其中Job Shop调度问题[1]（即单件车间作业计划调度问题）是一类与实际生产调度密切相关的调度问题，其研究具有重要的理论意义与工程实用价值，因此它也是目前研究最为广泛的车间调度问题[2]。经典的Job Shop调度问题多是静态调度问题，然而在实际车间生产中，工件多是动态到达的，且与工件相关的特征都是随时间变化的，这类问题即所谓的动态Job Shop调度问题。对于工件动态到达的动态Job Shop调度问题，仿真调度为主要研究方法之一。由于工件动态到达的动态Job Shop 调度问题通常是对应于面向订单（MTO-make to order）的制造系统，因此，交货期的设置对于这类问题的研究来说非常重要。

现有的交货期设置方法有多种，包括考虑工件特征信息（如总加工工时、总工序数等）的静态规则和综合考虑工件信息与车间状态信息（包括工件到达时系统中已有的工件数量、工件到达时在它的加工路径上的工件数等）的动态规则[3]。静态规则有总工时规则TWK（Total Work Content）、等裕量规则CON（Constant allowance for all jobs）、等松弛规则SLK（Equal slack for all jobs）、工序数量规则NOP（Number of operations）等；动态规则有系统工件数量规则JIS（Job in system）、队列工件数量规则JIQ（Job in queue）、队列总工时规则WIQ（Work in queue）等。这些规则中，以TWK规则被认为是交货期设置的最好方法[4]，也是所有的交货期设置方法中使用最为广泛的方法之一。记工件Jj的投放时间为rj，工件的总工时为Pj（含装设时间），根据TWK规则，工件的交货期dj设置为：

式中乘子k即交货期宽裕度系数，其取值大小决定了交货期的松紧程度。

文献中常见的关于确定交货期宽裕度系数k的方法主要有以下三种：1) 各种仿真参数配置下均取一组相同的宽裕度系数。最常见的取值为在（2,3,4,5,6,7,8）中取两至四个值[5～11]，如文献[5]中，k的取值为2、4、6和8；文献[7]中，k的取值为4、6和8；文献[8]中，k的取值为4和8等。对于非交货期相关性能指标（如最大流程时间、平均流程时间等）的调度问题研究来说，k的大小对性能的影响不大[11]，因此这一方法是简单且可行的。2）不同车间利用率下取几组不同的宽裕度系数。由于交货期松紧程度与车间利用率密切相关[12]，因此在设置交货期宽裕度系数k时考虑不同车间利用率下取不同的值。如文献[11]中，针对80%车间利用率，宽裕度系数的一组不同松紧程度的取值为k=(2.5,5.0,7.5,10.0)，而在90%车间利用率下，宽裕度系数的取值分别为k=(5.0,10.0,15.0,20.0)。这一种方法考虑了车间环境对交货期的影响，更为合理，但对于交货期松紧程度的评判，尚未考虑具体的指标。3) 以某个基准调度规则进行仿真调度，根据拖期工件百分比的几个不同级别，确定宽裕度系数取值。如文献[13]以FCFS（First come first server）为基准规则，按拖期工件百分比大致为1%、10%、20%三个等级确定宽裕度系数；而文献[14]则选用SPT（Shortest processing time）为基准规则，按拖期工件百分比5%和20%分别确定相应的紧和松的宽裕度系数。这一方法引入拖期工件百分比为指标，对交货期松紧程度进行了定量化的评判，但相关文献的研究中并未考虑不同的车间利用率。

许多文献中的试验都表明，车间利用率是影响交货期性能的主要参数[5]。当车间利用率较低时，较小交货期宽裕度系数即可对应于较松交货期；当车间利用率较高时，较大的交货期宽裕度系数也可能对应于较紧交货期。因此本文将对后两种方法进行综合，并在基准调度规则和评判标准方面进行了一定的改进，研究了面向交货期相关性能指标的动态调度问题仿真研究中宽裕度系数的确定方法；探索了不同拖期工件百分比下宽裕度系数随车间利用率变化的内在规律。

1 基准规则选择及评判标准的确定

1.1 基准规则的选择

已有的关于交货期宽裕度系数研究的文献中，通常选择一些简单规则作为基准进行仿真调度。最常用的规则为调度规则性能比对中使用的标杆规则，如SPT规则和FIFO（First-in first-out）或FCFS规则。然而，这些规则中不包含交货期相关的任何信息，且对如拖期时间等交货期相关的性能指标来说性能不佳。因此，由此确定的宽裕度系数所反映出的松紧程度对许多含交货期信息的规则（如EDD，earliest due date；MDD，modified due date，ODD，earliest operation due date；RR，rule by Raghu and Rajendran等）来说是偏松的。本文中，为研究面向交货期相关性能指标的动态调度问题仿真研究中宽裕度系数的确定方法，我们选择三个最常用的含交货期信息的简单规则，即EDD、MDD和ODD作为基准规则。

1.2 评判标准的确定

衡量交货期松紧程度的指标通常为拖期工件百分比，即完工时间大于设定交货期的工件的数量占所有工件的百分数，记为 T % 。文献[13]选用了三个级别，即 T % 大致为1%、10%、20%；文献[14]选用选择了两个等级，T%≈5%和T%≈20%，大致对应于松交货期和紧交货期两种情况；而文献[3]中则明确提到交货期的紧（tight）、中等（moderate）和松（loose）三个级别，其对应的拖期工件百分比 T % 分别为50%、25%、10%。可见，对交货期松紧程度目前尚无统一的标准。由于交货期松紧程度本身即是一个模糊概念，因此在本文的研究中，我们以一个范围作为松紧程度的评判标准，具体的评判标准取定为：T%=0%～10%对应于松交货期，T%=10%～30%对应于中等交货期，T%＞30%对应于紧交货期。

2 试验设计

工件陆续到达的Job Shop调度问题是一种典型的动态车间作业调度问题。本文将针对此类问题进行仿真调度试验，以探索在不同车间利用率和不同交货期松紧程度下宽裕度系数的设置问题。

2.1 仿真案例生成方法

仿真试验案例中有10台机器，工件总数为3000个，以指数分布形式到达车间。每个工件的工序数量从离散均匀分布DU[3,6]中产生。工件的工艺路线随机生成，每道工序的加工机器以相同概率按无放回抽样方式从10台机器中产生。每道工序的加工工时从离散均匀分布DU [5,15]中产生，因此每道工序的平均加工时间p=10个单位时间。

车间利用率 Ug用平均工件到达率l来控制。当工件动态到达的时候，根据文献[3,8]，此时车间利用率 Ug的表达式为：

给定一个车间利用率（如 Ug=80%，90%，95%），即可计算出每批工件到达的时间间隔tv。不失一般性，假设第一批工件的到达时间为0，则根据时间间隔tv可计算出每批工件的到达时间，即投放时间ri。

文献中常见的仿真试验设置的车间利用率从50%到97%变化不等。本文从其间选取了9种典型的车间利用率，研究交货期宽裕度系数对交货期松紧程度的影响并对其进行定量的仿真研究。

关于宽裕度系数k，试验取值范围设置为（2，50），以增量2进行递增。然后根据拖期工件百分比，确定不同车间利用率下合理的交货期宽裕度系数k的取值。

2.2 试验过程、数据获取与处理

为了使抽样统计的样本更加接近实际，需要进行多次统计计算平均值，本文中，进行从50%～97%共9种利用率下的仿真调度，每种车间利用率下生成20个仿真案例，考虑车间稳定状态和所采集数据的有效合理性，截除前后各500个工件[6]，采集20次仿真[16]在三个调度规则EDD、MDD和ODD下的拖期工件百分比，第i次仿真结果分别记

则的完工时间，RULE取值为上述三个调度规则。

记拖期工件百分比的总体均值为 T % ，由下式计算：

3 试验结果及分析

为分析不同车间利用率和不同交货期松紧程度下交货期宽裕度系数的合理取值，基于Java语言开发了相应的仿真调度系统，并在JBuilder集成开发环境下进行了仿真运行，得到了相应的仿真试验结果，并进一步对结果进行了分析。

3.1 试验结果

经过仿真试验 ，我们得到在不同车间利用率下，选取不同交货期宽裕度系数k时的拖期工件百分比 %T 。结果如表1和图1所示。

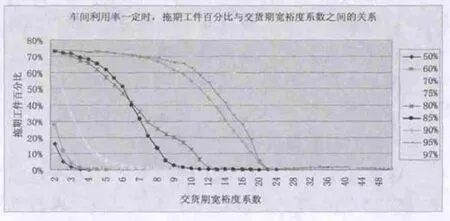
图1 不同 gU 下， %T 随k变化的曲线

3.2 结果分析

从所得曲线图可以看出，当车间利用率一定时，拖期工件百分比随着交货期宽裕度系数的增大而减小。即在设置交货期时，按TWK方法，若取较小的宽裕度系数k，则会出现较多的拖期工件；反之，若取较大的k值，则拖期工件会较少。因此可以根据需要选取不同的交货期宽裕度系数值。另一方面，比较不同车间利用率下的曲线可发现，当交货期宽裕度系数一定时，车间利用率较小的车间中的拖期工件较少，而车间利用率较大的车间中拖期工件较多。这进一步证实了车间利用率是影响交货期的重要因素，因此在设置交货期时，可根据不同车间利用率设置不同松紧程度的交货期。发动机性能信息重叠，提高计算速度。

表1 典型 gU 下取不同k时的 %T

[1] 张海军,左洪福,梁剑.航空发动机多指标模糊信息熵的性能排序研究[J]. 应用科学学报,2006,24(3):288-292.

[2] 杨皓翔,梁川,侯小波.改进的TOPSIS模型在地下水水质评价中的应用[J].南水北调与水利科技,2012, (5):51-55.

[3] 肖淳,邵东国,杨丰顺.基于改进TOPSIS法的流域初始水权分配模型[J].武汉大学学报（工学版）,2012,45(3):329-334.

[4] Karimi M, Moztarzadeh F,Pakzad A. Application of Fuzzy TOPSIS for Group Decision making in Evaluating Financial Risk Management, 2012[C].Malacca, Malaysia,2012 International Conference on Innovation, Management and Technology Research (ICIMTR2012),2012:215-218.

[5] 栾圣罡.基于气路参数样本的航空发动机状态监控监视方法与系统研究[D]. 哈尔滨:哈尔滨工业大学,2008.

[6] Karimi M, Moztarzadeh F, Pakzad A. Application of Fuzzy TOPSIS for Group Decision making in Evaluating Financial Risk Management,2012[C].Malacca, Malaysia,2012 International Conference on Innovation, Management and Technology Research (ICIMTR2012),2012:215-218.

[7] 陈可嘉,于先康.逆向物流服务供应商选择的ANP方法及Super Decisions软件实现[J].福州大学学报（自然科学版）,2012,40(1):31-37.