基于理论计算与有限元分析的偏心轴设计校核
2014-07-11童小冬邱东峰
童小冬 邱东峰
(安徽惊天液压智控股份有限公司,安徽 马鞍山 243000)
1 概述
铲斗式破碎装置[1]如图1(a)所示是采用复摆型破碎机理。 所谓复摆型破碎机理,是指动颚板在纵向断面内的运动轨迹处处不同,其上部近似为圆形,下部为椭圆形,主要用于对物料的粗、中破碎,具有结构简单,生产能力较高,对物料挤压和磨削作用较好,破碎产品质量较高等特点[2]。动颚部件如图1(b)所示相对机架定颚运动是产生破碎的动力源,动颚部件中的偏心轴是主要受力与力传递零件,偏心轴的设计结构与强度直接影响整机结构强度,下面将从理论分析对其结构进行设计,采用理论计算与有限元分析相结合对设计的偏心轴进行强度校核,对偏心轴结构设计合理性进行验证与评判。
2.1 强度设计校核理论[3][4]

图1 铲斗式破碎装置结构组成图
动颚的受力分析如图2 所示,破碎力P 垂直作用于距悬挂点B 的距离为(l 为动颚下端至悬挂点B 的总长度)的K 点上,推力板在不计重力的情况下,其对动颚的推力T 的作用线通过铰接点A、C;破碎力P 和推力T 的作用线相交于H 点;HB 为轴承反力 R 的作用线; 即破碎力 P、推力T 以及轴承反力R 交汇于H 点, 属于平面交汇力系,推力T 可分解为垂直于动颚的分力T1和平行于动颚的分力T2。

图2 鄂破机机构受力分析图

式中 β——推力板与动颚的夹角(传动角β=50°)
破碎铲斗的工作是间隙的, 破碎力P 是0~Pmax~0 脉动循环变化, 推力 T 及其分力 T1和 T2也遵循同一规律变化。
当轴承反力R 的分力R1通过曲柄OB 的回转中心O 时,另一分力R2对O 点的扭矩达到最大值,有力的平衡条件可知:

根据图2 所示的力系平衡条件可以得出式(2):
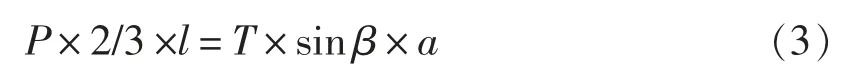
式中 P —— 破碎力 (前面已经确定Pmax≈1255.4),kN
l —— 动颚悬挂点到动颚齿板下端距离(l=115),cm
a——动颚悬挂点到推力板支撑点间的距离(a=0.75×l),cm
根据式 (3) 可以计算出推力板推力 T≈1457 kN
再根据图2 所示的力系平衡条件可以得出式(4):

根据式(4)可以计算出轴承反力R≈947 kN
以上计算将作为零部件设计与校核的依据。
2.2 偏心轴设计计算
偏心轴是一个传递扭矩,且两轴承支承间为偏心结构的转轴,对于它的可靠性设计,实际上就是根据预先拟定的结构方案, 确定一组直径,使之既能满足强度与刚度要求,又能满足可靠性要求, 而且重量轻、 结构合理以及经济效益好。
2.2.1 偏心轴结构设计
偏心轴的输入功率为:Pλ= η1N,其中 η1为 V带传动效率(取η1=0.95)
即:Pλ=η1Nmax=0.95×35≈33.25(kW)
(1)偏心轴最小直径 dmin确定

其中C=110 取(与轴的材质有关),已知参数Rλ、n2代入式(5)可得到:

考虑到轴上键槽会消弱轴的强度, 若为单键,则应将上述计算值dmin增大5%左右;若为双键,应将上述计算值dmin增大10%左右。 该设计轴为双键所以将上述计算的dmin增大10%,得到:dmin× 1.1=54.4×1.1≈59.8(mm)
(2) 偏心轴的各段直径与长度设计如图3。

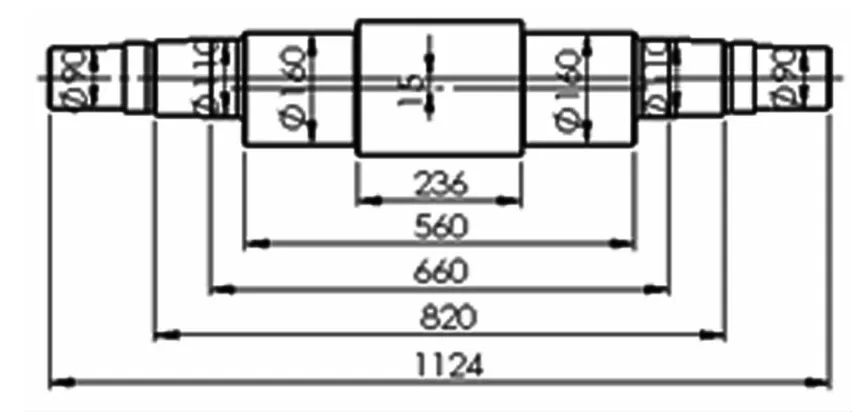
图3 偏心轴设计安装结构图
2.2.2 偏心轴理论校核
破碎铲斗在破碎工作时,破碎力通过动颚轴承传到偏心轴上,由于该破碎力很大,轴上其它零件传递的载荷相对来说就显得微不足道了,所以计算时可把这些载荷忽略不计,而只考虑破碎力产生的弯矩作用,破碎力平均分布在两个动颚轴承上;其次是带轮传递的扭矩,偏心轴在工作时受力为弯扭组合(如图4 所示)。
由分析图可以看出在B、C 处为弯扭组合最大截面, 为危险截面。 在B、C 截面产生的弯矩为

图4 偏心轴受力分析图
因为是单向回转,所以扭转切应力视为脉动循环变应力,折算系数为κ=0.6。
按第三强度理论,计算弯曲应力:

将已知参数代入式(6)可以得出:

偏心轴的材料为42CrMo(调质处理),危险的截面直径 D=160(mm),根据式(7)可以验证偏心轴是否符合使用要求。

将已知参数代入式(7)可以得出:

所以偏心轴设计符合强度要求。
2.3 偏心轴有限元分析
采用 SolidWorks 中的 Simulation 插件对偏心轴进行静力学分析,分析步骤如下[5]:首先根据设计尺寸建立偏心轴三维模型,定义偏心轴材料类型为42CrMo, 然后对机架支承轴承位置进行约束,对动颚板支承轴承位置施加力(轴承反力R),对带轮联接处施加扭矩Tλ,最后进行网格划分运行分析,分析后得到应力、应变、位移、安全系数分析图如下:
从以上分析图中可以看出偏心轴在正常工作时的应力、应变、位移以及安全系数情况,从图5、6 中得到偏心轴应力应变较小,与理论计算相吻合;图7 中所示为位移情况,中间位移最大,约为0.24(mm);图8 为安全系数分布图,最小安全系数约为1.55;综合以上分析图可以得出偏心轴设计完全满足实际工作需求。
3 结束语
通过强度理论指导偏心轴整体设计,结合实际安装结构要求进行局部细化设计,设计完成后再利用理论计算方式对设计的偏心轴进行校核验算,并利用有限元仿真软件对设计的偏心轴进行静力学仿真分析,理论计算校核结果与仿真分析结果一致,验证偏心轴设计结构合理,强度要求达到使用要求。 本文采用的理论指导产品设计,并以理论计算与有限元软件分析相结合方式对设计产品进行校核,为同类产品设计方法提供借鉴。
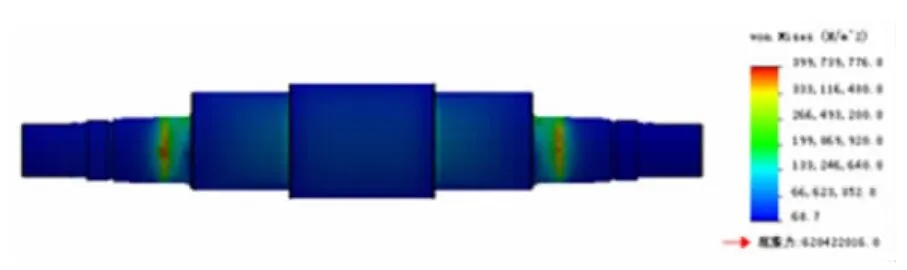
图5 偏心轴应力分析图

图6 偏心轴应变分析图

图7 偏心轴位移分析图

图8 偏心轴安全系数分析图
[1]童小冬.基于颚破原理的新型工程机械破碎输具研发设计[J].凿岩机械气动工具,2012,(2):9~12.
[2]廖汉元.颚式破碎机优化设计[M].北京:机械工业出版社.1998.
[3]初明智.复摆颚式破碎机的动颚行程计算[J].机械工程与自动化,2005,(2):62~64.
[4]戴少生,王旦容. 复摆型颚式破碎机的功率计算(一)[J].水泥装备,2001,(5):20~22.
[5]江孔华,李春树,孙晓东.CosmosWorks 软件在复杂结构梁分析中的应用[J].机械工程师,2003,(7):40~42.
