一类不确定T-S模糊系统的H∞控制器设计

张 莹

(沈阳大学师范学院,辽宁沈阳 110044)

一类不确定T-S模糊系统的H∞控制器设计

张 莹

(沈阳大学师范学院,辽宁沈阳 110044)

基于线性矩阵不等式的方法,研究了一类带有不确定参数的T-S模糊系统的H∞控制器设计问题.给出了参数不确定的T-S模糊系统的系统建模以及系统的二次稳定性,并且对此类T-S模糊系统的H∞控制问题进行了探讨,给出了新的基于状态反馈H∞控制器的设计方法.

线性矩阵不等式(LMIs);T S模糊系统;二次稳定;H∞控制;状态反馈

T S模糊系统模型是在局部线性模型的基础上通过隶属函数得到的非线性模型,由“如果—则”规则描述,可以通过模糊规则给出非线性系统的局部线性表出,因此,借助线性系统的理论和方法,很多学者对T-S模糊系统进行了分析和研究[111],其中多数研究的T-S模糊系统模型中,每个子系统的系数矩阵是确定的.而本文给出的T-S模糊系统,则是系数矩阵带有实参数的不确定系统.

1 一类参数不确定的T-S模糊系统

本文给出如下带有实参数的T-S模糊模型所描述的非线性系统.

系统的模糊规则k:若ω1(t)是Fk1,ω2(t)是Fk2,…,ωn(t)是Fkn,则

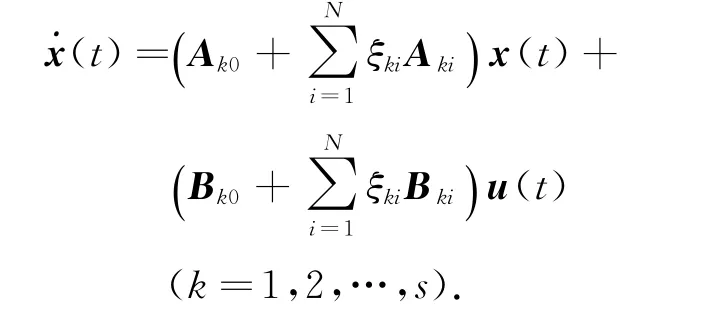
式中,Fkj是模糊集;ω(t)=[ω1(t),ω2(t),…, ωn(t)]T是可测系统变量,是前件变量;x(t)∈Rn是状态变量;u(t)∈Rm是控制输入变量;s为模糊规则数;ξki(k=1,2,…,s;i=1,2,…,N)是不确定的实参数,且满足0≤ξki≤α,α为给定的正数; Aki,Bki(k=1,2,…,s;i=0,1,…,N)是系数矩阵.

模糊系统的整个状态方程为

式中,

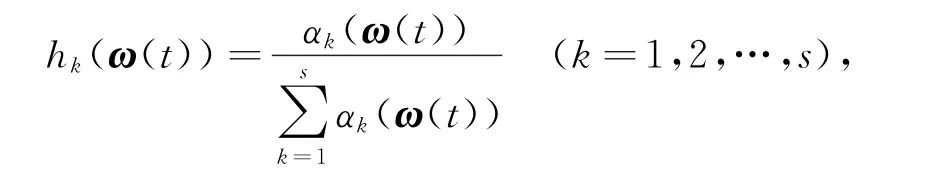
对于不确定模糊系统(1),当控制输入变量为0时,如果存在正数d和一个正定矩阵X,对于V(x(t))=x(t)TXx(t),有˙V(x(t))≤ -d x(t)Tx(t)成立,则T-S模糊系统(1)被称为二次稳定[12]的.

引理[12]若存在正定对称矩阵P,使得下式成立:

则存在状态反馈控制器

使得闭环系统

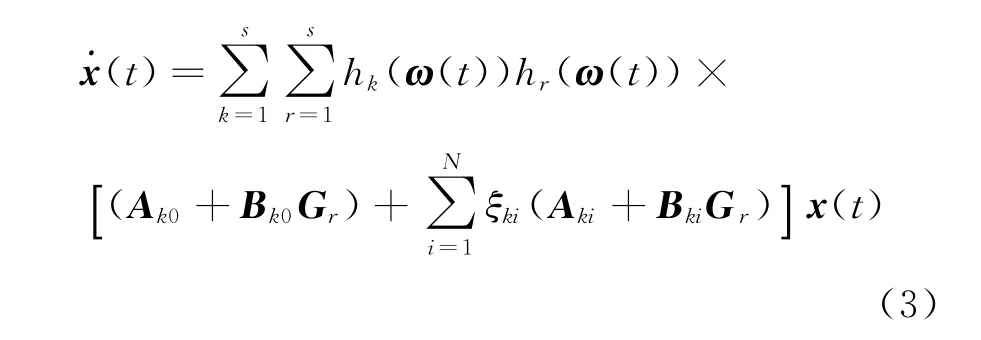
当控制输入变量为零时是二次稳定的.其中

2 不确定T-S模糊系统的H∞控制器设计

由二次稳定性,研究如下带有实参数的不确定模糊系统:

对于T-S模糊系统(4),设计状态反馈控制器(2),使得当w(t)≡0时,闭环系统是二次稳定的;且在零初始条件下,对于给定的正数γ,对于任意的外界干扰输入w(t)∈L2[0,+∞),控制输出z(t)满足‖z(t)‖2≤d‖w(t)‖2.其中,0＜为L2范

式中,w(t)∈Rq是平方可积的干扰输入变量;Ck, Dk(k=1,2,…,s)是适当维数的常数矩阵;z(t)∈Rp是控制输出变量.数.

此时称T-S模糊系统(4)的H∞范数小于γ.

定理 对于给定的正数γ,如果存在矩阵Gr(r=1,2,…,s)和对称正定矩阵P,使得下式成立:

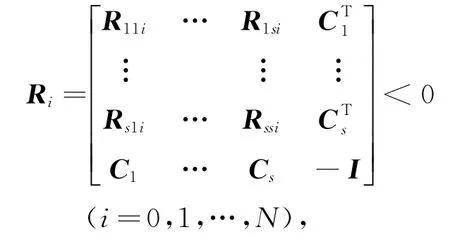
则对于系统(4),状态反馈(2)产生的如下闭环系统的H∞范数小于γ:

式中,

证明 设Xkki=Aki+BkiGk,2Xkri=Aki+ BkiGr+Ari+BriGk.

先证当w(t)≡0时,闭环系统是二次稳定的.

由引理和Schur补公式,容易得到

令V(x(t))=xTPx,则

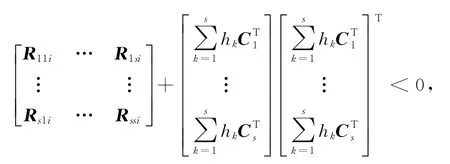
所以

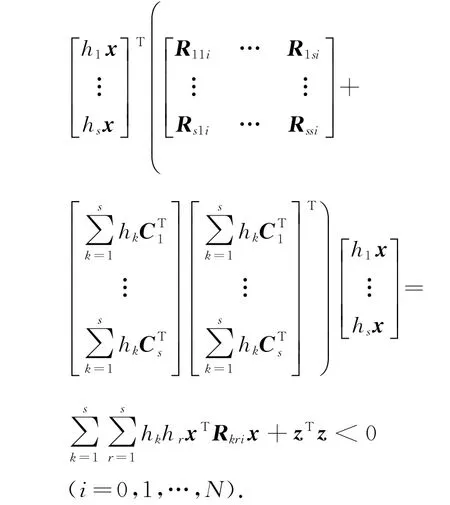
因为存在正数di＞0(i=0,1,…,N),使得

所以

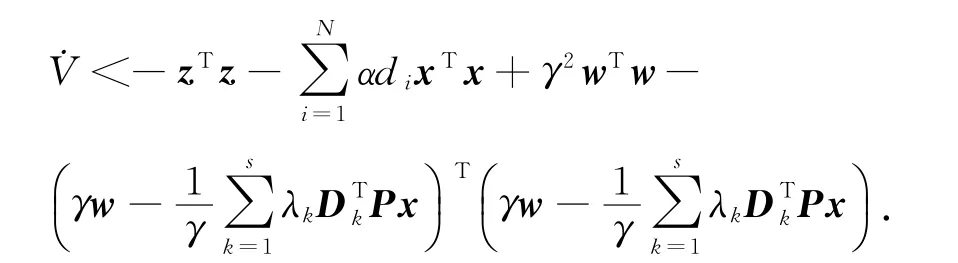
由x(0)=0,则V(x(0))=0.上式两端对t从0到+∞积分,得推论 对于给定的正数γ,若存在正定对称矩阵Q及矩阵Er(r=1,2,…,s),使得下式成立:

则状态反馈(2)产生的闭环系统(5)的H∞范数小于γ,且Gr=ErQ-1(r=1,2,…,s).其中

3 结 语

本文主要针对带有实参数的一类不确定T-S模糊系统,给出了系统的模型,不确定性体现在模糊系统的状态方程系数矩阵中带有实参数.由系统的二次稳定性,对系统的基于状态反馈的H∞控制问题进行了研究,应用线性矩阵不等式(LMIs)给出了一个新的状态反馈H∞控制器的设计方法.

[1]Tanaka K,Sugeno M.Stability Analysis and Design of Fuzzy Control Systems[J].Fuzzy Sets and Systems, 1992,45(2):135-156.

[2]Feng G,Cao G,Rees W.An Approach to H∞Control of a Class of Nonlinear Systems[J].Automatic,1996,32 (10):1469 1474.

[3]Tanaka K,Ikeda T,Wang H O.Robust Stabilization of a Class of Uncertain Nonlinear Systems via Fuzzy Control: Quadratic Stabilizability,H∞Control Theory,and Linear Matrix Inequalities[J].IEEE Transactions on Fuzzy Systems,1996,4(1):1 13.

[4]Cao S G,Rees N W,Feng G.H∞Control of Nonlinear Continuous Time Systems Based on Dynamical Fuzzy Models[J].International Journal of Systems Science, 1996,27(9):821-830.

[5]Yakubovich V A.The S-procedure in Nonlinear Control Theory[J].Vestnik Leningrad University:Mathematics, 1977(4):73-93.

[6]佟绍成,王涛,王艳平,等.模糊控制系统的设计及稳定性分析[M].北京:科学出版社,2004:15-32.

(Tong Shaocheng,Wang Tao,Wang Yanping,et al.The Design and Stability Analysis of Fuzzy Control System [M].Beijing:Science Press,2004:15 32.)

[7]Lee K R,Jeung E T,Park H B.Robust Fuzzy H∞Control for Uncertain Nonlinear Systems via State Feedback:An LMI Approach[J].Fuzzy Sets and Systems,2001,120 (1):123-134.

[8]Zhang J M,Li R H,Zhang P A.Stability Analysis and Systematic Design of Fuzzy Control Systems[J].Fuzzy Sets and Systems,2001,20(1):65 72.

[9]Liu X D,Zhang Q L.New Approaches to H∞Controller Designs Based on the Fuzzy Observers for T-S Fuzzy Systems via LMI[J].Automatic,2003,39(9):1571-1582.

[10]Liu X D,Zhang Q L.Approaches to Quadratic Stability Conditions and H∞Control Designs for T-S FuzzySystems[J].IEEE Transactions on Fuzzy Systems,2003, 11(3):830 839.

[11]Zhang Ying,WangYanan.Quadratic Stability and H∞Control of a Class of Uncertainty T-S Fuzzy Systems[C]∥23rd Chinese Control and Decision Conference(CCDC 2011).Mianyang,2011:3493 3496.

[12]Zhai Ding,Zhang Ying.Robust H∞Controller Design for Uncertainty Fuzzy Systems[C]∥21st Chinese Control and Decision Conference(CCDC 2009).Guilin, 2009:4143-4146.

H∞Control of T-S Fuzzy Systems with Real Parametric Uncertainty

Zhang Ying
(Normal School,Shenyang University,Shenyang 110044,China)

Based on linear matrix inequalities(LMIs),the problem of H∞control of a class of T-S fuzzy systems with real parametric uncertainty is studied.The model of the T-S fuzzy systems is given,as well as the conditions for quadratic stability.The conditions for H∞control are studied,and the new designing method of the state feedback H∞controller is presented.

linear matrix inequalities(LMIs);T-S fuzzy systems;quadratic stability;H∞control; state feedback

TP 13

A

【责任编辑:王 颖】

2095-5456(2014)02-0169-04

2014-01-02

张莹(1973-),女,吉林长春人,沈阳大学讲师.