钢卷仓库中的吊机调度问题
2014-04-27李彦平
谢 谢,李彦平
(沈阳大学 装备制造综合自动化重点实验室,辽宁 沈阳 110044)
本文的研究来源于钢铁企业冷轧原料库,所有存储在原料库的板卷等待被运走进行进一步的冷轧加工.由于存储技术的要求,这些板卷每个区域中每行必须按照两层堆放,下层的板卷数至少比上层多一个(如图1所示,图中以四行的区域为例).当下游生产或客户需求板卷时,存储在下层且没有被上层阻碍的需求板卷可以直接被吊机提起运输走;否则,在下层板卷被运走前,阻碍板卷首先被倒垛到该区域的其他空位置.所有需求板卷的运输和阻碍板卷的倒垛都由上方的移动吊机进行.实际中,一个仓库通常可以划分为许多相同的区域,每个区域上方有一台吊机,见图1.吊机从一个地方移动到另一个地方意味着它的提起设备(吊钩)随着吊机不仅沿着平行的跨移动而且在跨之间移动,两方向的移动是同时进行的.本文将吊钩看作吊机.
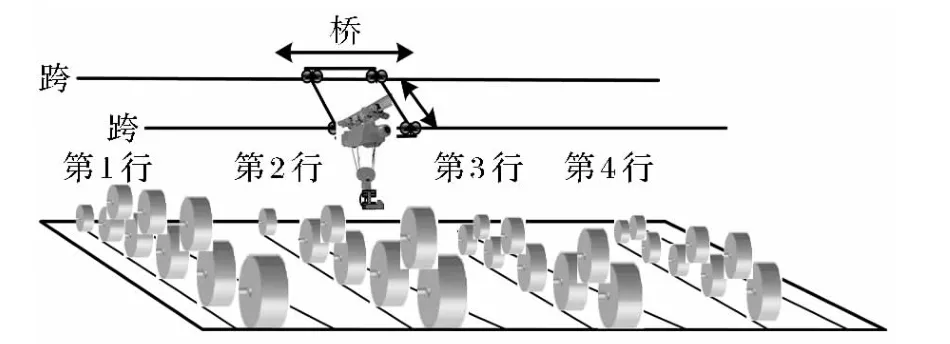
图1 钢卷仓库一个区域的板卷存储Fig.1 Coil storage in a block of steel coil warehouse
如果需求板卷被吊机直接运输到指定位置,将这个过程命名为吊机的运输;如果阻碍板卷被运输到该区域的其他位置,将这个过程命名为吊机的倒垛.本文主要提出并分析了吊机调度问题,同时将运输和倒垛结合起来考虑,以尽快确定全部需求板卷的运输顺序以及每个阻碍板卷的倒垛位置.该问题存在于实际中大多数仓库运输和生产系统(如钢铁企业中热轧后库、热镀锌原料库、酸洗原料库和酸轧后库,集装箱终端的垛场,造船厂的原料库),然而很少有这方面的相关研究,一个可能的原因是很难同时将吊机的运输和倒垛集成考虑.有效地将运输和倒垛集成可以增加吊机的利用率,减少这种贵重设备不必要的等待时间.
本文研究的问题为发生在仓库中的物质处理设备(吊机)的活动:尽快地接收、排序和转移(确定板卷的顺序),这种活动属于由van den Berg和Zijm[1]所定义的仓库管理活动.尽管 Zäpfel和Wasner[2]考虑了仓库内关于实际顺序、调度和移动的路线,他们将存储位置和吊机作为机器,并把问题描述成一个一般性的车间调度问题,但并没有给出仓库活动中吊机运输和倒垛的细节.此外,他们主要提出了一个启发式,并没有从计算复杂度的角度对其进行评价并给出理论分析.
在自动存/取仓库环境中,相关文献主要考虑了生产布局设计问题,其中,Burkard等[3]考虑了自动仓库中车辆操作系统的设计.仓库的布局和车辆的数目及属性已经给定.除了van den Berg[4]给出的关于仓库问题的综述,van den Berg和Zijm[1]讨论了仓库系统并提出了仓库管理系统的一个分类.van den Berg[4-5]研究了在库存控制决策和生产分配分发关系的模型.Bertazzi和Speranza[6]为极小化总库存和运输费用而考虑了库存和运输费用的关系.
包含倒垛操作的文献较多地出现在集装箱终端和钢铁企业的堆垛问题中.由于每垛中一个板坯放在另一个板坯的顶端,因此,每个需求板坯仅被一个板坯阻碍,因此,这类问题比本文研究的问题要简单.在集装箱取出顺序给定的情况下,Kim和Hong[7]提出了一个分支定界过程和一个启发式算法决策集装箱的存储位置以最小化倒垛数目.为求解集装箱的动态存取问题,Wan等[8]提出了一个线性整规划模型和启发式.在集装箱的取出顺序给定的前提下,Lee等[9]提出了一个三阶段启发式以最小化加权总移动次数和吊机的工作时间之和.Lee和Hsu[10]提出了一个线性整规划模型以最小化倒垛次数.Lee和Chao[11]通过邻域搜索的启发式求解了该问题更大规模的实例.Steenken等[12]给出了关于堆垛问题理论和实际的综述.
本文的问题不同于上面提到的设计仓库形状、设计存取设备的路线等问题,以上问题并没有考虑吊机上提下放的细节操作.尽管一些学者关于吊机调度研究了吊机的倒垛或重倒垛活动,但对于板卷的倒垛研究得很少.尽管谢和李[13]研究了钢铁企业中的吊机调度问题,但他们并没有同时考虑吊机的运输和倒垛.因此,有必要研究这种将运输和倒垛集成考虑的吊机调度.
1 问题描述和符号
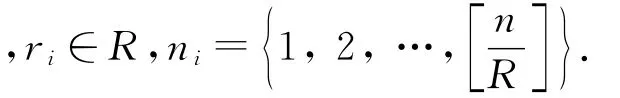
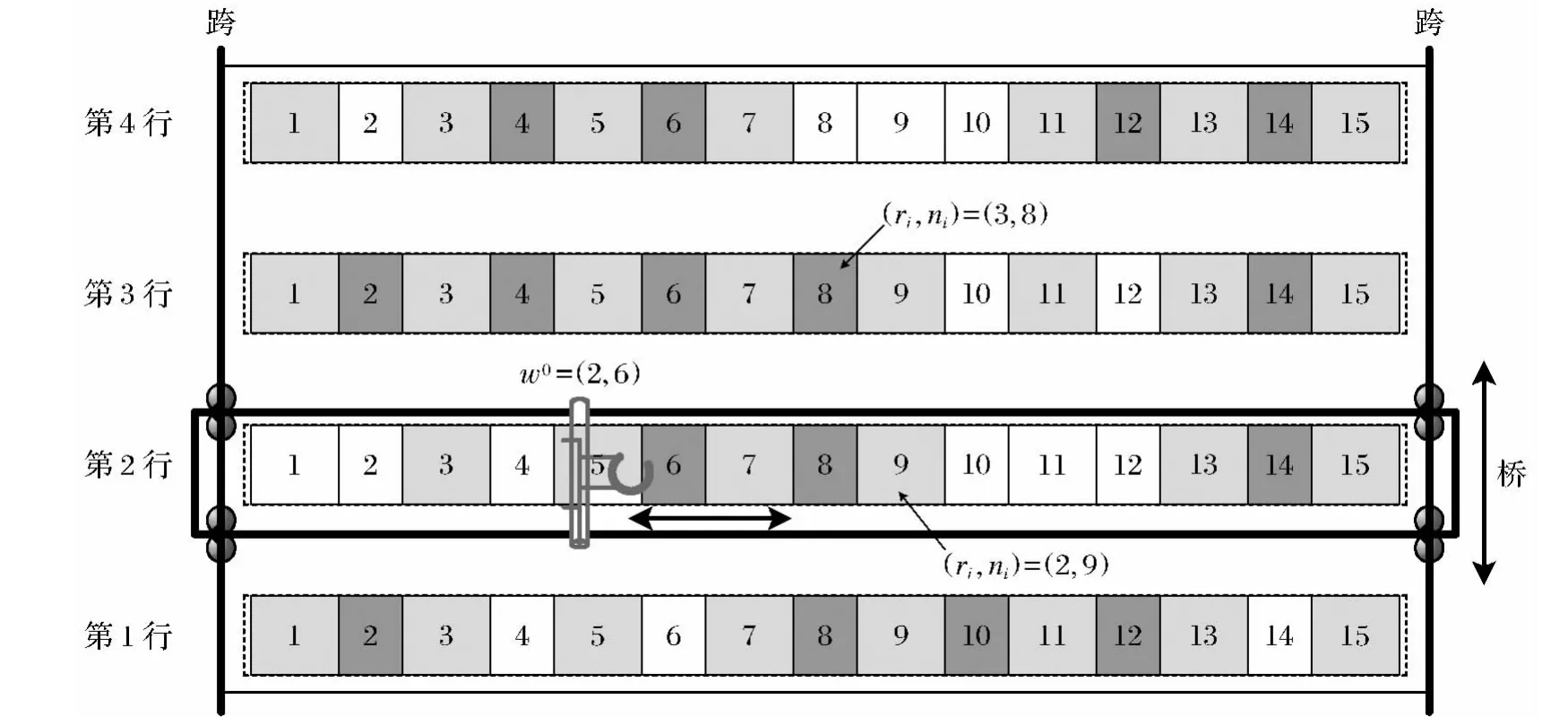
图2 钢卷仓库一个区域的俯视图Fig.2 Top view of a block in steel coil warehouse
定义吊机的位置等于它的吊钩向工作区内投影与之距离最近的板卷位置.令w0为吊机的初始位置.定义全部板卷指定的位置为wT.因此,吊机最初的位置与板卷Ji的距离可以表示为=|w0-wi|,板卷Ji与指定位置的距离可以表示为di=|wi-wT|.类似的,两板卷Ji和Jj之间的距离可以表示为dij=|wi-wj|.
定义吊机上提、下放板卷的时间为μ(很容易扩展到上提下放的时间是不同的情况).吊机带着板卷沿着平行跨和支撑桥之间移动的速度分别为v1和v2,类似的,两个方向空吊机移动的速度为λ1(λ1≥v1)和λ2(λ2≥v2).由于给定了可计算的移动距离和吊机的速度,因此,吊机的每一个装载移动时间和空移动时间分别由下面两式计算出来:
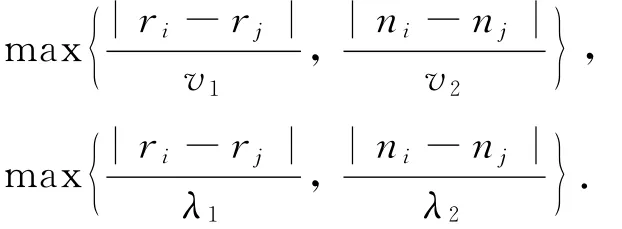
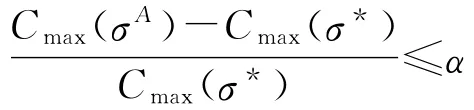
2 问题模型
为了更清楚地描述问题,本文提出了问题的一个混合整线性规划模型(MILP).
2.1 问题参数
输入数据如下:
wi,w0和wT分别对应板卷的位置、吊机的初始位置和指定位置,一旦给定N 个需求的板卷,它们的位置已知;
μ对应于吊机上提和下放一个板卷;
v1,v2和λ1,λ2对应于吊机带着板卷和不带板卷移动沿着两个方向移动的速度,为了表达方便,本文中,令λ=min{λ1,λ2},v=min{v1,v2},不失一般性,假设λ≥v≥1;
M是一个很大的正整数.
决策变量如下:
xij=1,如果板卷Ji被吊机倒到板卷Jj的位置(Ji,Jj∈Ω0);否则,xij=0;
si,吊机从板卷Ji的位置移动的开始时间(Ji∈Ω 或Ji∈Ω0);
ei,吊机将板卷Ji(Ji∈Ω0)倒垛后的结束时间;
Cmax,最后一个板卷运到指定位置的完成时间.
2.2 数学模型
问题的模型可以表示为
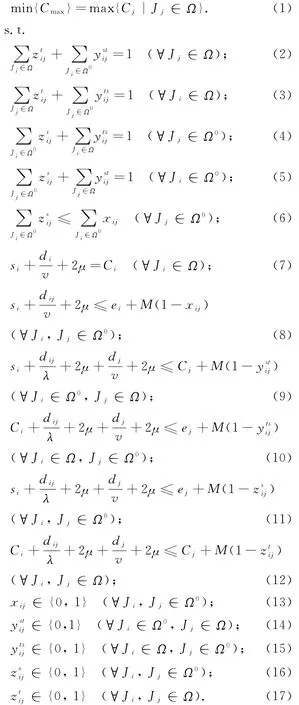
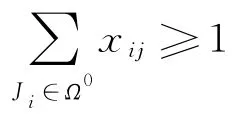
3 复杂性及问题的性质
根据前述可知,该问题的复杂性仍然未知.因此,通过与一个已证明为强NP难的问题相归结,证明该问题也是强NP难的.
3.1 复杂性
定理1 考虑运输每个需求板卷的时间趋近于0,将这个时间近似地认为0,即使是这种简单情况,问题也是强NP难的.
证明 当这种情况存在时,只需要考虑所有的阻碍板卷.给定任意一个旅行商问题的例子,将旅行商看作一台吊机,将城市看作阻碍板卷的位置.这台吊机从初始位置开始,必须通过每个阻碍板卷的位置将它们运走.由于两个板卷之间的距离和速度都是预先已知的,因此,这个问题等价于已经证明为强NP难的旅行商问题.这种情况可解当且仅当旅行商问题可解.
推论 本文研究的问题是强NP难的.
证明 在倒垛和运输同时考虑的情况下,可知本文研究的问题是强NP难的.
复杂性的结果表明,除非P=NP,否则问题不存在多项式时间内可解的算法.在下一部分中,首先证明了满足最优解的一些性质.
3.2 问题的性质
图3描绘了一行的侧视图,其中,深色圈代表需求的板卷.

图3 板卷仓库中一行的侧视图Fig.3 Side view of a row in steel coil warehouse
根据板卷的位置,将需求板卷集Ω分成如下四类.
第1类 位于上层的板卷(见图3中板卷2和14),令Ω1表示这类板卷的集合.
第2类 板卷位于下层,被需求板卷阻碍(包含在Ω1中的板卷阻碍)或无其他阻碍板卷(见图3中板卷5和15),令Ω2表示这类板卷的集合.
第3类 板卷位于下层且被一个板卷阻碍(见图3中板卷7被板卷8阻碍,板卷17被板卷18阻碍,板卷21被板卷20阻碍),令Ω3表示这类板卷的集合3表示阻碍板卷的集合.
第4类 板卷位于下层,且被不包含在Ω1中的两个板卷阻碍(见图3中板卷11被板卷10和12阻碍,板卷19被板卷18和20阻碍),令Ω4表示这类板卷的集合4表示阻碍板卷的集合.
因此,根据定义,有Ω=Ω1∪Ω2∪Ω3∪Ω4.注意一些阻碍板卷或许同时阻碍两个需求板卷,如板卷J18和J20,每一个属于阻碍板卷集3或4,即3∩4≠Ø.根据分类表示,Ω1和Ω2中的板卷可以直接运输.为了运输Ω3和Ω4中的板卷,阻碍板卷必须先被倒垛到一个位置,这个位置或者是下层的空位,或者是上层空位在它的下层已有两个板卷占着位.
性质1 最优调度中,最大完工时间不少于需求板卷与指定位置之间的总移动时间.
证明 由于一个调度开始并终于这个单吊机操作,调度值等于吊机总倒垛与总移动时间总和,因此,性质显然成立.
证明 根据板卷的分类,至少有|Ω3|≤|Ω3|+2|Ω4|个板卷需要倒垛.如果|Ω3|≤|Ω1|+|Ω2|,那么每个|Ω3|中的板卷可以仅倒一次到|Ω1|+|Ω2|的位置.总倒垛次数为|Ω3|.否则,至少一个板卷需要倒两次.因此,为了运输所有的需求板卷,总倒垛次数至少为|Ω3|.类似的,最多(|Ω3|+2|Ω4|)个板卷需要倒垛.如果(|Ω3|+2|Ω4|)中的板卷每个仅倒一次,则需要(|Ω3|+2|Ω4|)次;否则,一个板卷最多需要倒n次.因此,最多的倒垛次数为n(|Ω3|+2|Ω4|).
3.3 特殊情况
在这部分中,首先分析吊机之间可以将所有需求板卷运走的情况.这种情况发生在需求板卷在仓库中上层和没有阻碍板卷的下层.
性质3 如果所有需求板卷均在Ω1和Ω2中,最优调度可以在o(N)内,通过选择(-di)最小的板卷为第一个板卷,剩余的N-1个板卷顺序任意排列而得到.
证明 令σ=[J1,J2,…,JN]为板卷按任意顺序的标号.在这个调度中,吊机从它的初始位置空移动到J1,放下吊钩后将它提起立即运到指定位置.一旦吊机到达指定位置,将这个板卷放下,从这个位置空移动到板卷J2的位置.放下吊钩后将J2提起立刻移动到指定位置当下,立刻空移动到板卷J3,运输J3.重复这个过程,直到JN被吊机运输到指定位置.吊机移动的完工时间可以用下式表示:
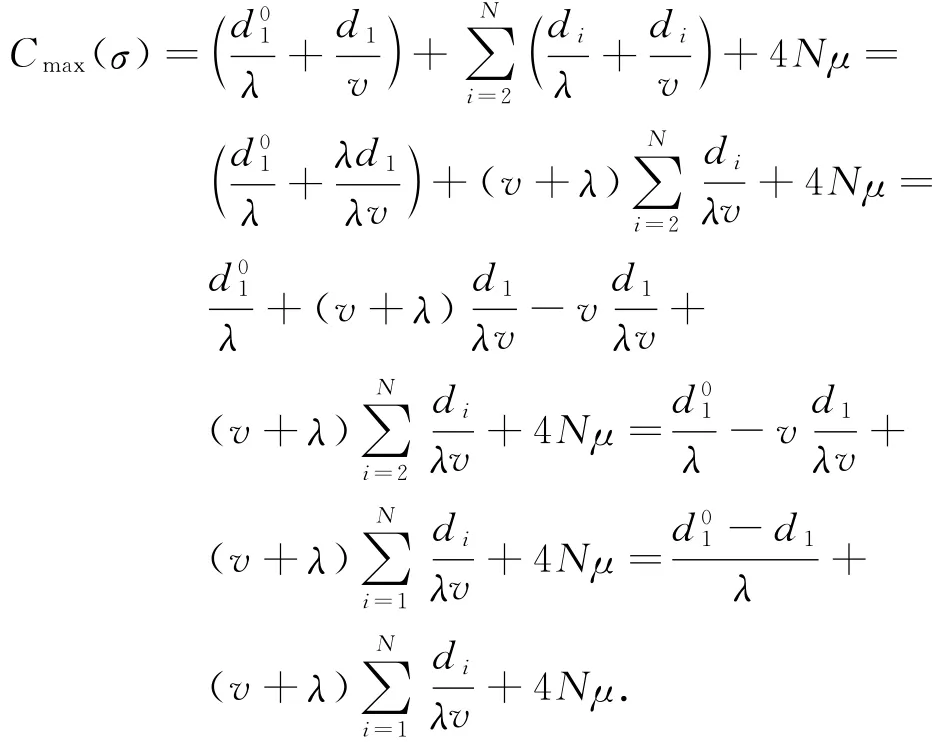
由于上式最后两项是常数,最小化Cmax(σ)等价于选择(-di)的值最小的板卷.
4 一般情况的启发式算法及其性能分析
由于本文研究的问题是强NP难的,线性规划模型求解问题的缺陷就是获得解的时间随着问题规模的增大快速增加.相比之下,启发式算法在计算时间和解的质量上给出了合理的折中.
4.1 启发式算法
第1步 运输所有属于Ω1和Ω2中的板卷,根据性质3,选择具有最小-di)的板卷作为第一个板卷,剩余的|Ω1|+|Ω2|-1板卷调度顺序任意.转第2步.
第3步:
②吊机从当前位置到集合Ω中的板卷距离与该板卷到指定位置距离之和.
比较由①和②得到的距离,选择最小的进行吊机操作.如果这两个距离相等,则选择Ω1∪Ω2中的板卷优先于3∪4.如果对于集合3∪4中的任意一个板卷没有可倒垛的位置,转第1步,运输当前在集合Ω1∪Ω2中的板卷.一旦集合Ω中的板卷都被运输到指定位置,停止.
根据启发式,由第1步,吊机运输板卷的时间为o(NlogN).由第2步,吊机首先将阻碍板卷倒走再运输所有的板卷.由于总倒垛板卷为(|Ω3|+2|Ω4|)≤3 N,倒垛位置为|Ω0|=n,因此,总倒垛时间为o(Nn(logN)(logn)).由第3步,吊机倒垛和运输操作或许交替进行.因此,由启发式算法获得调度的时间为o(Nn(logN)(logn)).
4.2 性能分析
令启发式算法获得的调度为σH.
性质4 问题的下界LB可以从如下两个界中获得:
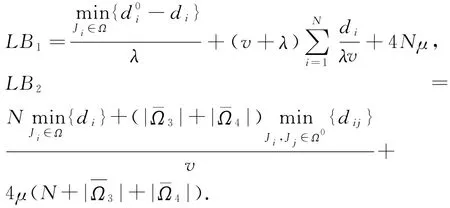
其中,LB=max{LB1,LB2}.
如果所有的需求板卷都在集合Ω1和Ω2中,根据性质3,LB1为最优目标值.LB2为总倒垛与运输时间的最小值.
由于单吊机必须运输所有的需求板卷并为所有的阻碍板卷倒垛,因此,最大完工时间依赖于吊机的操作顺序.启发式的目的就是尽可能减小吊机运输和倒垛操作的距离.由于启发式包括所有可能的情况,因此,按照如下三种情况分析最坏性能.
情况1 Ω=Ω1∪Ω2.
在这种情况下,所有需求板卷属于集合Ω1和Ω2,应用启发式第1步可以得到最优调度σ*,调度值为Cmax(σ*).因此
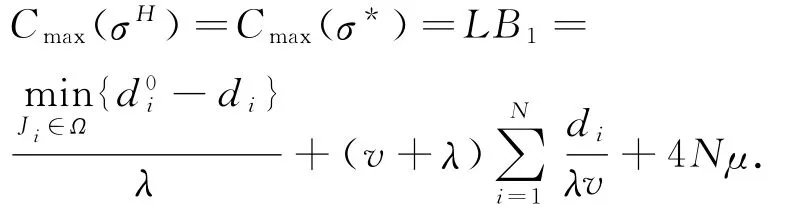
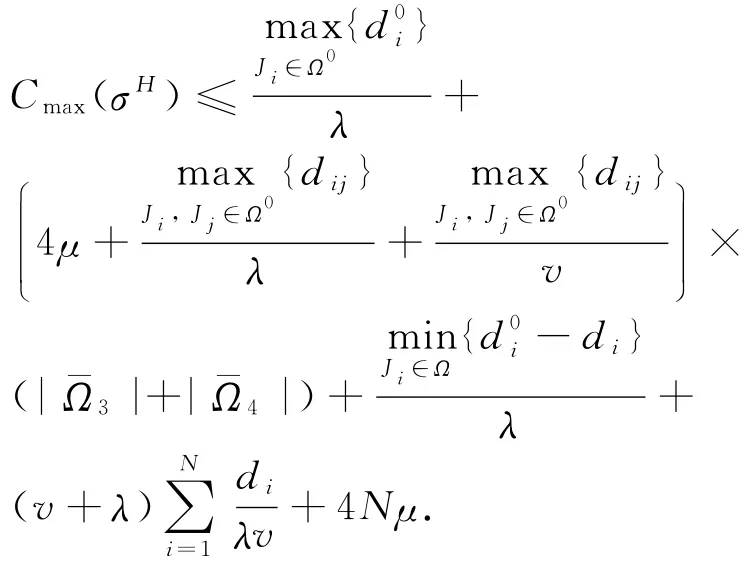
式中,右边前两项为最长倒垛时间总和,后三项为运输所有需求板卷最短的时间总和.
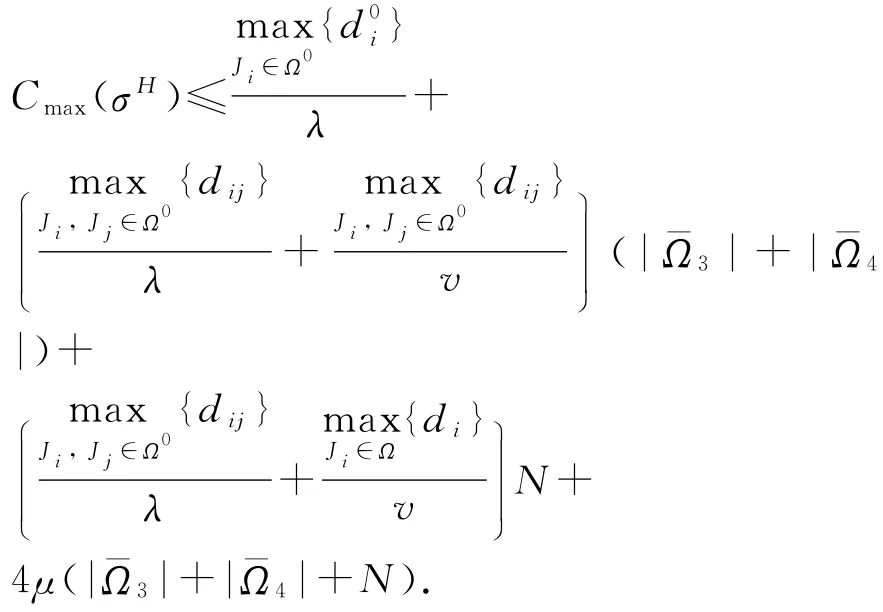
式中,右边第一项是吊机从初始位置空移动的最大时间,第二、第三项是吊机倒垛操作和运输操作的最大时间,第四项为吊机总的上提和下放的时间.
根据情况2和Cmax(σ*)≥LB≥LB2,同时结合|Ω3|≤N、|Ω4|≤2 N 和λ≥v≥1,可以得到如下最坏情况比:
根据情况3和Cmax(σ*)≥LB≥LB2,同时结合|Ω3|≤N、|Ω4|≤2 N 和λ≥v≥1,可以得到如下最坏性能比:因此,max{(a),(b)}为最坏性能的比值.
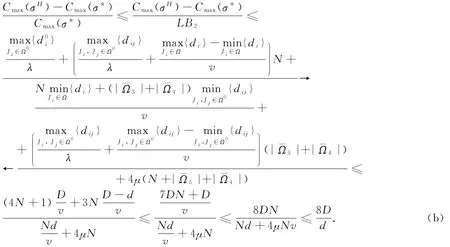
定理2 对于由启发式得到的问题的任意一个调度σH,最坏性能保证为
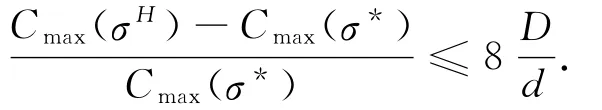
这个比值是潜在的最坏情况,与距离参数有关.
5 结 语
本文重点考虑了吊机调度问题以将所有下游阶段生产或客户需要进一步加工的需求板卷运输到指定位置的最大完工时间最小化.这个问题源于实际工业中的仓库管理问题,而且实际中经常发生.研究这种吊机调度问题的文献很少.本文主要提出了算法并从理论性能的角度对这个问题进行了分析,可以用于企业仓库管理和大型设备使用以获得更有效的利用率.
未来的研究方向包括解决如下问题:其他的目标函数如平均完工时间、总延迟时间和延迟板卷的个数;板卷具有可替换约束和板卷间的优先约束.关于多吊机调度问题,是未来的另一个研究方向.
[1] van den Berg J P,Zijm W H M.Models for Warehouse Management: Classification and Examples [J].International Journal of Production Economics,1999,59(1/2/3):519-528.
[2] Zäpfel G,Wasner M.Warehouse Sequencing in the Steel Supply Chain as a Generalized Job Shop Model[J].International Journal of Production Economics,2006,104(2):482-501.
[3] Burkard R E,Fruhwirth B,Rote G.Vehicle Routing in an Automated Warehouse:Analysis and Optimization[J].Annals of Operations Research,1995,57(1):29-44.
[4] van den Berg J P.Planning and Control of Warehousing Systems[D].Enschede:University of Twente,1996.
[5] van den Berg J P.A Literature Survey on Planning and Control of Warehousing Systems[J].IIE Transactions,1999,31(8):751-762.
[6] Bertazzi L,Speranza M G.Minimizing Logistic Costs in Multistage Supply Chains[J].Naval Research Logistics,1999,46(4):399-417.
[7] Kim K H,Hong G P.A Heuristic Rule for Relocating Blocks[J].Computers & Operations Research,2006,33(4):940-954.
[8] Wan Y W,Liu Jiyin,Tsai P C.The Assignment of Storage Locations to Containers for a Container Stack[J].Naval Research Logistics,2009,56(8):699-713.
[9] Lee Yusin,Lee Y J. A Heuristic for Retrieving Containers from a Yard[J].Computers & Operations Research,2010,37(6):1139-1147.
[10] Lee Yusin,Hsu N Y.An Optimization Model for the Container Pre-marshalling Problem[J].Computers &Operations Research,2007,34(1):3295-3313.
[11] Lee Yusin,Chao S L.A Neighborhood Search Heuristic for Pre-marshalling Export Containers[J].European Journal of Operational Research,2009,196(2):468-475.
[12] Steenken D,VoßS,Stahlbock R.Container Terminal Operation and Operations Research:A Classification and Literature Review[J].OR Spectrum,2004,26(1):3-49.
[13] 谢谢,李彦平.罩式退火过程中的多吊机调度问题[J].沈阳大学学报:自然科学版,2012,24(1):12-19.
(Xie Xie,Li Yanping.Multi-Crane Scheduling in Batch Annealing Process[J].Journal of Shenyang University:Natural Science,2012,24(1):12-19.)
