三级倒立摆的GA－PIDNN系统辨识

张秀玲，樊红敏，臧佳音，赵 亮

（1.燕山大学 河北省工业计算机控制工程重点实验室，河北 秦皇岛 066004；2.国家冷轧板带装备及工艺工程技术研究中心，河北 秦皇岛 066004）

倒立摆作为一个多变量、不稳定、非线性、强耦合的复杂系统，被公认为自动控制理论中的典型实验设备，也是控制理论教学和科研中不可多得的典型物理模型［1－4］.倒立摆本身是一个自然不稳定体，在控制过程中能有效地反映控制中的许多关键问题，如非线性问题、系统的鲁棒性问题、跟踪问题及镇定性问题等［5－6］.

对于诸如三级倒立摆这样的多变量、非线性系统，由于系统变量之间的耦合作用和非线性关系，其辨识问题比单变量系统更为复杂，成为研究的难题［7］.基于神经网络的系统辨识方法是一种简单有效的一般性方法，它不需要过多的有关待辨识系统的先验经验，它是通过训练和学习，对网络连接权值进行修正以达到系统辨识的目的，为非线性系统的辨识提供了一条十分有效的途径［8］.

PIDNN是一种多层前向神经网络，它除了具备传统的多层前向网络的特点，如逼近能力、并行计算、非线性变换特性等［9］，其隐含层还分别具有比例（P）、微分（I）和积分（D）神经元，即不仅有具备静态非线性映射功能的比例元，还有可处理动态信息的积分元和微分元［10］.积分元和微分元的引入，使作为数学基石的、反映客观世界规律的微积分概念与神经元网络的基本单元融合为一体，增强了神经元处理信息的能力，充实和完善了神经元的种类，使神经网络的行为更加丰富多样［11］.另外，PIDNN还融合了PID控制算法和神经网络的优点，隐含层神经元的个数固定，网络结构简单，在辨识复杂动态系统时不需要任何附加环节.所以，PIDNN特别适合于非线性动态系统的辨识.

GA是一种不依赖于具体问题的直接搜索方法，具有全局寻优的特点.利用GA对PIDNN的权值进行优化，可以有效防止寻优过程收敛于局部最优解［12］.

结合PIDNN和GA的优点，本文提出了基于GA－PIDNN实现非线性三级倒立摆系统辨识方案.GA－PIDNN以PIDNN为基础，通过GA来训练和学习PIDNN的权系数，既保留了GA的全局搜索能力，又具有神经网络的鲁棒性和自学习能力，还利用了PIDNN优于一般多层网络的动态特性和无须任何附加环节的优点.

1 三级倒立摆的工作原理

三级倒立摆装置形象直观，结构简单，构件组成参数和结构易于改变，其系统主要由控制对象、水平滑轨、伺服电机、皮带轮、传动带以及电气测量装置组成.控制对象由小车、上摆杆、中摆杆及下摆杆组成［6］.

三级倒立摆装置的结构组成如图1所示.

图1 三级倒立摆的结构组成Fig.1 Structure of the triple inverted pendulum

规定顺时针方向的转角和力矩为正.约定记号如下：u为外接作用力，x 为小车的位移，θi（i＝1，2，3）分别为下摆杆、中摆杆和上摆杆与铅垂线方向的夹角.三级倒立摆的实验参数如表1所示.

表1 三级倒立摆的实验参数Table 1 Experiment parameters of the triple inverted pendulum

在忽略掉空气阻力、静摩擦等次要因素后，将三级倒立摆抽象为一个由小车、均匀质量的摆杆和质量块组成的刚性系统.小车可以在水平滑轨上左右平移，摆杆可以在铅垂面内运动，摆杆间由质量块自由连接［13－14］.将其置于坐标系后，三级倒立摆的简化结构如图2所示.

2 PIDNN结构设计与工作过程

2.1 PIDNN结构设计

PIDNN分为单输出PID神经网络（SPIDNN）和多输出PID神经网络（MPIDNN）.SPIDNN基本形式为2×3×1结构，MPIDNN由多个SPIDNN子网交叉并联而成.MPIDNN的输入层至隐含层是按子网独立的，而隐含层至输出层则是交叉连接的，这种交叉连接使整个MPIDNN结合为一体.MPIDNN的结构形式如图3所示.

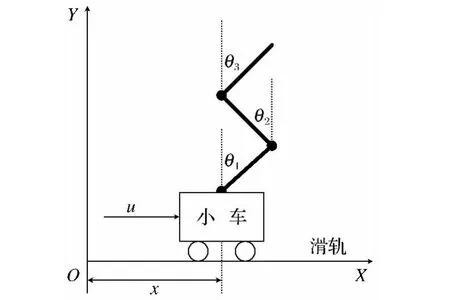
图2 三级倒立摆的简化结构Fig.2 Simplified structure of the triple inverted pendulum

图3 MPIDNN的结构Fig.3 Structure of MPIDNN

2.2 PIDNN工作过程

MPIDNN输入层的2n个神经元的输入输出状态分别为［8］

式中，s为子网的序号，s＝1，2，…，n.

MPIDNN的隐含层由3n个神经元构成，即n个比例元、n个积分元和n个微分元，它们的输入总值的计算公式均为

式中，i为子网的输入层神经元序号，i＝1，2；wsij为输入层至隐含层的连接权重值；j为子网的隐含层神经元序号，j＝1，2，3；有上标“′”的变量表示隐含层变量.

隐含层比例元、积分元、微分元的状态分别如下所示：

隐含层各个神经元的输出均为

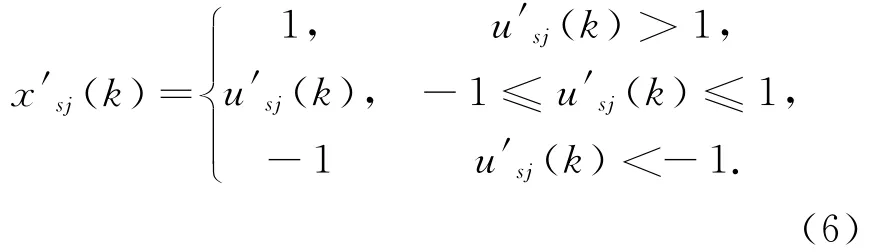
MPIDNN的输出层有m 个神经元，其输出为

式中，h 为输出层神经元序号，h＝1，2，…，m；w′sjh为隐含层至输出层的连接权重值；有上标“″”的变量表示输出层变量.

MPIDNN的目标函数为

3 GA-PIDNN的倒立摆辨识系统设计

3.1 PIDNN的GA优化

GA是一种借鉴生物界自然选择和自然遗传机制的随机全局搜索算法.它通过模拟自然进化过程来寻找最优解，其本质是一种高效、并行、全局搜索的方法［15－16］，而传统的 BP算法易陷入局部极小，无法实现全局优化.

本文PIDNN的优化中，GA采用实数编码方法.选择初始群体的大小为20，交叉概率为0.8，变异概率自适应调整范围为0.01～0.1.GA初始群体中的各个个体用均匀分布的随机数来生成，算法以求适应度函数，即目标函数J的最小值训练学习的准则和目的［17］.

GA有三个基本操作：选择、交叉和变异.GA－PIDNN优化过程的流程如图4所示.

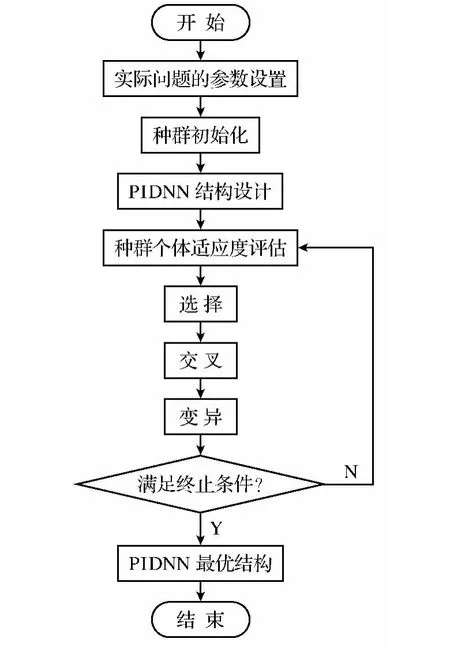
图4 GA－PIDNN的优化过程Fig.4 The optimization procedure of GA－PIDNN

首先，将实际问题进行参数设置，即编码，随机地形成初始种群；然后，进行PIDNN的结构优化设计，在对初始种群个体适应度检测评估后，通过选择、交叉、变异操作不断循环，直到达到终止条件，得到最优解，即得到神经网络的最优结构.GA－PIDNN优化得到的最终结果如图5所示.

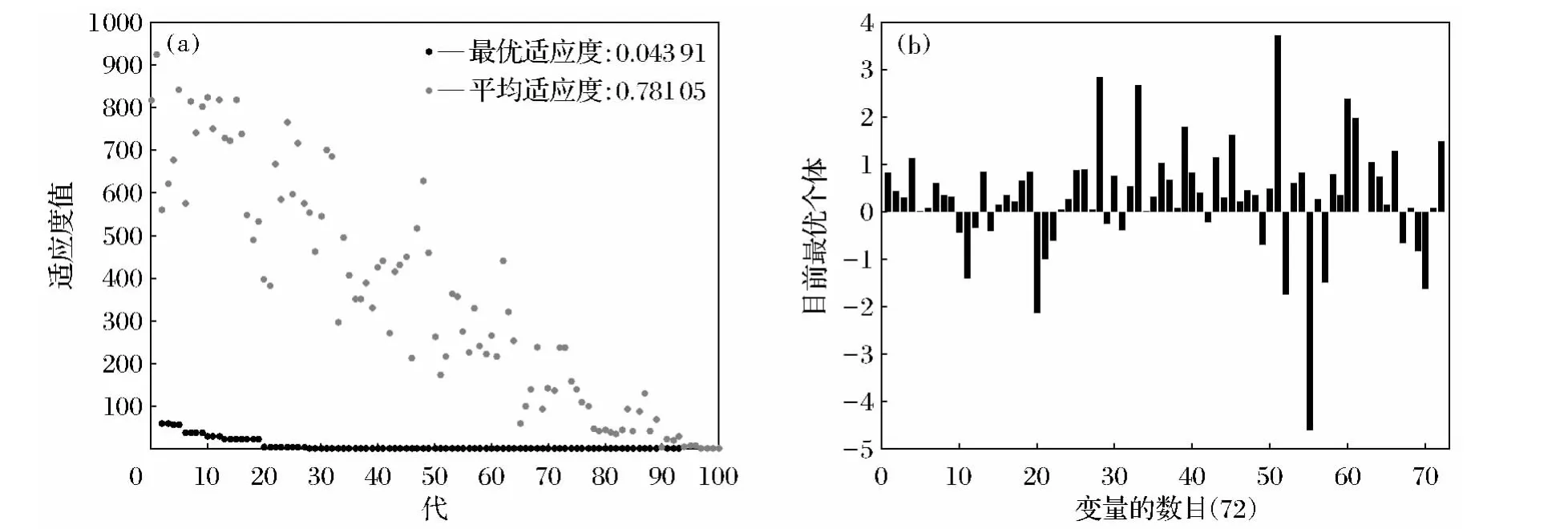
图5 GA－PIDNN优化结果Fig.5 The optimization results of GA－PIDNN

3.2 GA－PIDNN辨识系统设计

GA－PIDNN在进行系统辨识时，与一般的神经网络一样，通过直接学习被辨识系统的输入输出数据，利用GA优化网络的权值，使所要求的函数值达到最小，从而总结出隐含在系统输入输出中的关系，用GA－PIDNN逼近被辨识系统.

GA－PIDNN辨识系统如图6所示.

图6 GA－PIDNN辨识系统框图Fig.6 The identification system diagram of GA－PIDNN

图6中，y1、y2、y3，y4分别表示小车的位移以及下摆杆角度、中摆杆角度、上摆杆角度的实际输出值，y′1、y′2、y′3，y′4为相应变量的辨识器输出值.

非线性三级倒立摆系统有1个输入u，4个输出x、θ1、θ2、θ3，因此，GA－PIDNN 辨识网络应为MPIDNN，其需要4个SPIDNN子网交叉并联［9，18］，构成8×12×4结构，包含72个权值，其中，输入层至隐含层有24个权值，隐含层至输出层有48个权值.

GA－PIDNN辨识系统网络结构如图7所示.

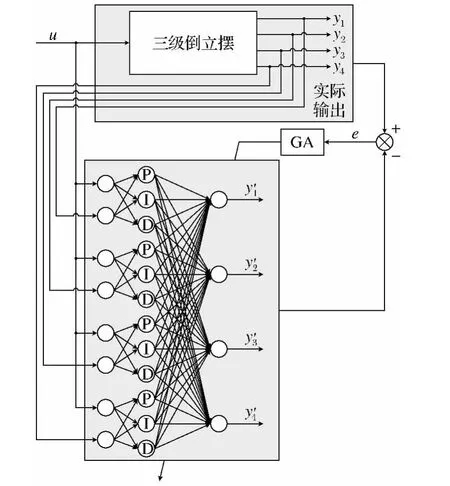
图7 GA－PIDNN辨识系统网络结构Fig.7 Identification structure of GA－PIDNN

图7中，e为实际输出与辨识网络输出之间偏差的绝对值.

4 仿真验证

为了验证GA－PIDNN非线性三级倒立摆系统辨识的有效性，根据文献［14］得到的精确的、完全的、非线性的三级倒立摆模型，获得实时输入输出数据，作为学习样本，进行网络训练.

仿真结果如图8所示.

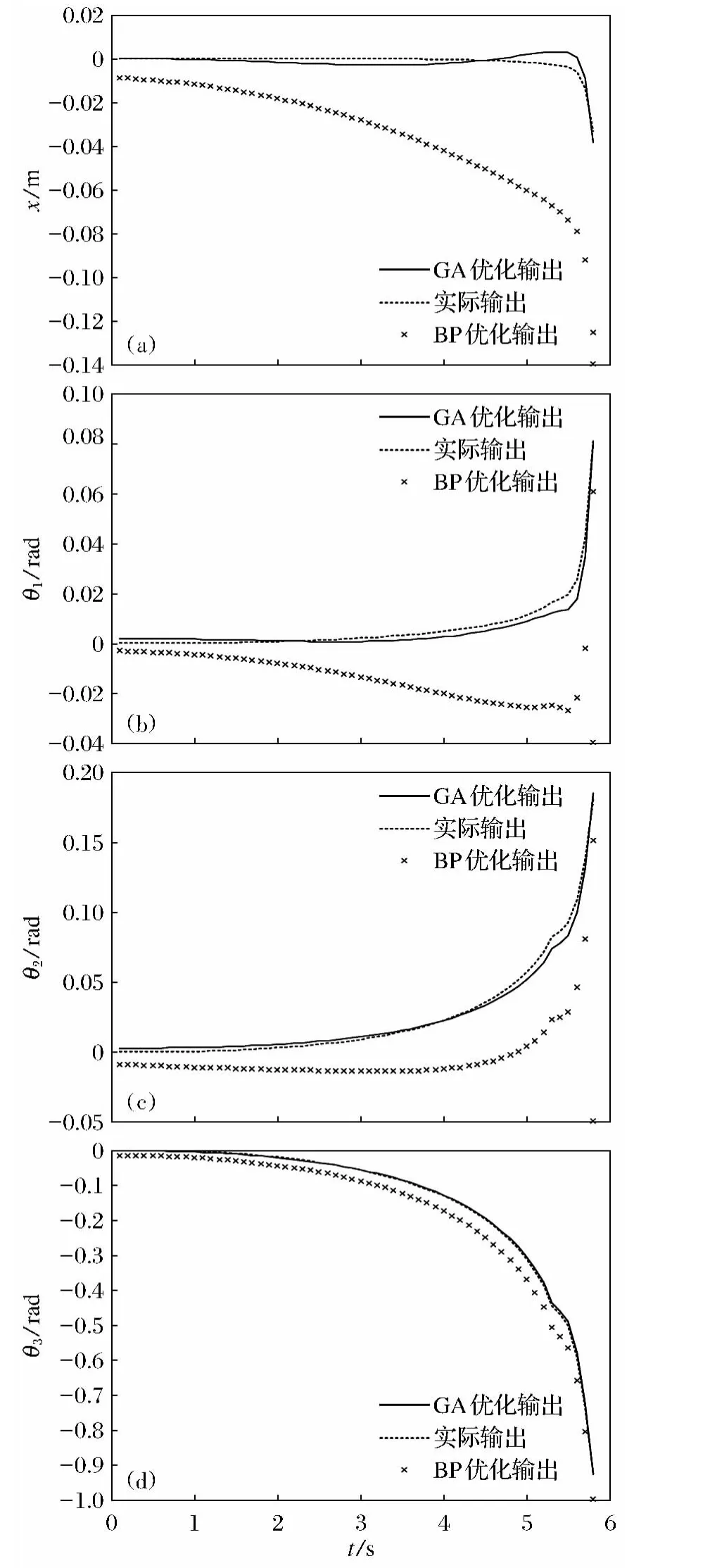
图8 GA－PIDNN辨识结果Fig.8 Identification results of GA－PIDNN

图8a～图8d分别为小车位移、下摆杆角度、中摆杆角度、上摆杆角度辨识结果的拟合曲线.从图8的每一个图中可以直观地看出，经过GA优化的PIDNN辨识得到的输出响应曲线非常接近于实际输出曲线，辨识精度明显高于BP算法优化的PIDNN.

5 结 语

本文针对非线性三级倒立摆装置，设计了GA－PIDNN辨识系统，建立了逼近其实际输入输出特性的动态网络，实现了精确的系统辨识，发挥了GA的全局寻优特点，对比表明了该算法的辨识精度明显优于BP算法，取得了较好的辨识效果.仿真结果表明，GA－PIDNN具有适应面广、收敛迅速、不易陷入局部极小点、结构简单等优点，具有很强的非线性动态系统辨识能力，是非常理想的系统辨识研究方法.

［1］ 李祖枢，但远宏，张小川，等.双摆机器人摆杆平衡态任意转换运动控制的实现［J］.自动化学报，2010，36（12）：1720－1731.

（Li Zushu，Dan Yuanhong，Zhang Xiaochuan，et al.Fulfillment of Arbitrary Movement Transfer Control between Equilibrium States for a Double Pendulum Robot［J］.Acta Automatica Sinica，2010，36（12）：1720－1731.）

［2］ Liu Bo，Hu Haiyan.Group Delay Induced Instabilities and Hopf Bifurcations，of a Controlled Double Pendulum［J］.International Journal of Non－Linear Mechanics，2010，45（4）：442－452.

［3］ Niemann H，Poulsen J K.Design and Analysis of Controllers for a Double Inverted Pendulum［J］.ISA Transactions，2005，44（1）：145－163.

［4］ Do K D，Seet G.Motion Control of a Two－Wheeled Mobile Vehicle with an Inverted Pendulum ［J］.Journal of Intelligent ＆ Robotic Systems，2010，60（3／4）：577－605.

［5］ Shu Huailin.Inverted Pendulum Control System Based on PID Neural Network［J］.Machine Tool ＆ Hydraulics，2008，36（3）：141－143，146.

［6］ Yi Jianqiang，Yubazaki N，Hirota K.Stabilization Control of Series－Type Double Inverted Pendulum Systems Using the SIRMs Dynamically Connected Fuzzy Inference Model［J］.Artificial Intelligence in Engineering，2001，15（3）：297－308.

［7］ 沈永俊，顾幸生.基于PID神经网络的非线性系统辨识与控制［J］.华东理工大学学报：自然科学版，2006，32（7）：860－863.

（Shen Yongjun，Gu Xingsheng.Identification and Control in Nonlinear System Based on PID Neural Network［J］.Journal of East China University of Science and Technology： Natural Science Edition， 2006， 32（7）：860－863.）

［8］ 舒华，舒怀林.基于PID神经网络的多变量非线性动态系统辨识［J］.计算机工程与应用，2006，42（12）：47－49.

（Shu Hua，Shu Huailin.Identify of Multivariable Nonlinear Dynamic Systems Based on PID Neural Networks［J］.Computers and Chemical Engineering，2006，42（12）：47－49.）

［9］ Shu Huailin，Pi Youguo.PID Neural Networks for Time－delay Systems［J］.Computers and Chemical Engineering，2000，24（2）：859－862.

［10］ 舒华，舒怀林.基于LabView的PID神经网络控制器设计与仿真［J］.系统仿真学报，2006，18（10）：2918－2920.

（Shu Hua，Shu Huailin.Development and Simulation of PID Neural Networks Controller Based on LabView［J］.Journal of System Simulation，2006，18 （10）：2918－2920.）

［11］ 舒怀林.PID神经元网络多变量控制系统分析［J］.自动化学报，1999，25（1）：105－110.

（Shu Huailin. Analysis of PID Neural Network Multivariable Control Systems［J］. Acta Automatica Sinica，1999，25（1）：105－110.）

［12］ 舒怀林.PID神经网络及其控制系统［M］.北京：国防工业出版社，2006：21－51.

（Shu Huailin.PIDNN and Control System［M］.Beijing：National Defense Industry Press，2006：21－51.）

［13］ 张秀玲，田力勇，张少宇.三级倒立摆的T－S型前馈补偿模糊神经网络控制［J］.模糊系统与数学，2011，25（4）：129－135.

（Zhang Xiuling，Tian Liyong，Zhang Shaoyu.Control of Triple Inverted Pendulum by Using Fuzzy Neural Network Combined with Feedforward Based on T－S Model［J］.Fuzzy Systems and Mathematics，2011，25（4）：129－135.）

［14］ Gao Junwei，Cai Guoqiang，Ji Zhijian，et al.Adaptive Neural－fuzzy Control of Triple Inverted Pendulum［J］.Control Theory ＆ Application，2010，27（2）：278－282.

［15］ 雷英杰，张善文，李续武，等.MATLAB遗传算法工具箱及应用［M］.西安：西安电子科技大学出版社，2005：5－30.

（Lei Yingjie，Zhang Shanwen，Li Xuwu，et al.MATLAB GA Toolbox and Application［M］.Xi'an：Xi'an University of Electronic Science and Technology Press，2005：5－30.）

［16］ Sedighi M，Afshari D.Creep Feed Grinding Optimization by an Integrated GA－NN System ［J］.Journal of Intelligent Manufacturing，2010，21（6）：657－663.

［17］ 张秀玲，徐腾，赵亮，等.基于GA－PID神经网络的板形模式识别方法［J］.沈阳大学学报：自然科学版，2013，25（3）：209－215.

（Zhang Xiuling，Xu Teng，Zhao Liang，et al.Method of Flatness Pattern Recognition Based on GA－PID Neural Network［J］.Journal of Shenyang University：Natural Science，2013，25（3）：209－215.）

［18］ 姚凌虹，尹鑫鹏，张重阳.三级倒立摆的加权变量模糊神经网络控制［J］.自动化技术与应用，2008，27（11）：7－10.

（Yao Linghong，Yin Xinpeng，Zhang Chongyang.Fuzzy Neural Network Control of a Triple Inverted－Pendulum Based on Weighted Variables ［J］. Techniques of Automation and Applications，2008，27（11）：7－10.）