基于动力学模型的弹道式再入弹道估计方法*

江晓东，谢京稳，郭军海

(北京跟踪与通信技术研究所，北京 100094)

0 引言

飞行器再入大气飞行的特点是速度快，并由于受到复杂的空气动力影响而呈现出强的非线性特性[2]。Julier和Uhlmann[3-4]等利用UT(unscented transform)变换，提出unscented Kalman filter(UKF)，由于不需要对非线性系统进行线性化，可有效地应用到非线性系统的状态估计中。文献[5-6]在再入目标弹道估计的背景下，对3种非线性滤波——扩展卡尔曼滤波(extended Kalman filter，EKF)，UKF和粒子滤波(particles filter，PF)的滤波性能进行了对比分析，从计算量、滤波性能和滤波的稳健性上综合考察，UKF是这3种滤波算法中最优的。

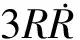
1 弹道式再入目标的动力学模型

弹道式再入飞行器在再入过程中只受到空气阻力和重力的作用，在地心惯性坐标系[7]下，其总加速度的表达式为[7]：

a=aD+aG+w,

(1)

式中:a为目标的总加速度；aD为空气阻力引起的加速度；aG为地心引力引起的加速度；w为系统状态噪声，假定服从高斯分布，其方差为模型设计参数。

在地心地固坐标系[7]下，加速度表达式在式(1)的基础上修正为

(2)

式中:ar为目标相对总加速度;ωe为地球自转角速度向量；p为目标的位置向量；v为再入体相对大气的速度向量；2ωe×v为科里奥利力引起的加速度；ωe×(ωe×p)为惯性离心力引起的加速度。

空气阻力的方向与目标相对于空气的速度矢量v相反，与空气密度ρ和目标速度v的平方成正比，空气阻力引起的加速度为

(3)

式中：uv=v/|v|为vr的单位向量；ρ(h)为空气密度，h为高程，本文中采用文献[8]提出的大气密度模型。

α(t)为阻力参数，其倒数β(t)=1/α(t)也称弹道系数。对弹道式再入飞行器来说，α(t)是一个非常重要的参数，它通常是未知变量，因此经常也将其作为待估状态参量，增加到运动状态向量中，使得状态向量从6维变为7维X=(x,y,z,vx,vy,vz,α)T。α(t)的建模方式有多种，适用于不同的环境。文献[7]对其模型进行了系统的总结。本文选用指数模型，即对阻力参数的比率γln(α/α0)进行建模：

α(t)=α0exp(γ(t)),

(4)

(5)

式中:ωγ(t)为高斯白噪声；α0为预先知道的典型阻力参数。这样，待估状态向量变为X=(x,y,z,vx,vy,vz,γ)T。这种建模方式需要先验信息α0，但保证了阻力参数恒正，这对于保证滤波的稳定性至关重要[3]。

基于式(1)和(3)，将加速度的矢量形式写成分量形式，整理可得

(6)

最后，基于方程(5)和(6)可得弹道式再入飞行器的动力学模型为

(7)

将此模型记为BRV-Exp模型，式(7)为变系数非线性常微分方程组，难以给出解析解，但可借助欧拉积分法或龙格库塔法给出数值解，以便进行状态参量的预测。

2 多台雷达的测量模型

单台雷达的测量模型[9]为

(8)

记为

Y1(k)=h1(X(k))+v1(k),

(9)

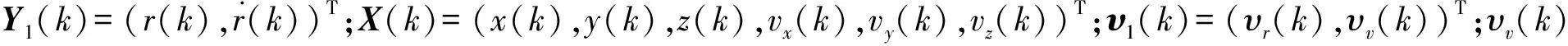
基于N台雷达的总测量模型为[10]

Y(k)=h(X(k))+v(k),

(10)

式中：Y(k)=(Y1(k),Y2(k),…,YN(k))T；

h(·)=(h1(·),h2(·),…,hN(·))T；

v(k)=(v1(k),v2(k),…,v3(k))T.

设v(k)服从正态分布N(0,R(k))，R(k)=diag(R1(k),R2(k),…,RN(k))，这样基于状态转换模型(7)和测量模型(10)，就可利用UKF进行再入目标的弹道估计了。

3 不敏卡尔曼滤波(UKF)

UKF是由Julier等人首先提出的。UT变换是UKF的基础，它通过构造一个确定的点集(Sigma点)，使得它与当前状态具有相同的统计特征，即均值和方差相同。具体来说，UT变换利用当前状态(均值和方差)构造点集{Xi(k)}，然后让每个点Xi(k)通过非线性方程，得到非线性变换后的点集{Yi(k)}，预测均值和方差可以在{Yi(k)}点集上求得。

设待估状态向量维数为L，则Sigma点的个数为一般为2L+1，为了增加Sigma点的个数，以提高估计精度，通常需要对状态向量进行扩维，扩维后的状态向量由目标状态向量，状态噪声和测量噪声组成，即Xa=(XT,vT,nT)。扩维UKF(augmented UKF，AUKF)算法流程如下[11]：

初始化：

(11)

(12)

(13)

(14)

计算Sigma点及其权值：

(15)

(16)

(17)

(18)

预测：

(19)

(20)

(21)

(22)

(23)

更新：

(24)

(25)

(26)

(27)

(28)

4 仿真结果与分析

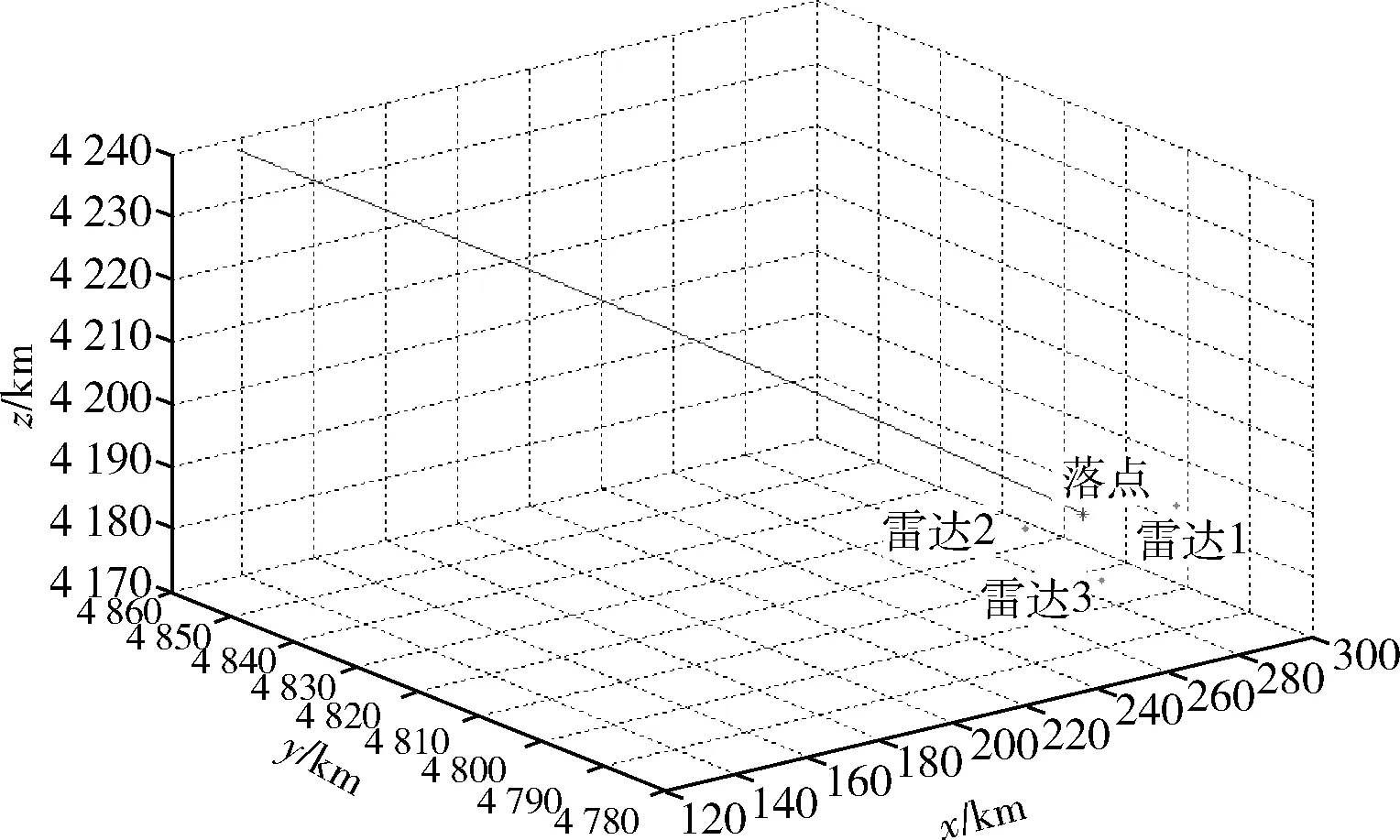
图1 再入目标的轨迹及测量雷达布局图Fig.1 Trajectory of re-entry target and measuring-radar layout

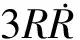
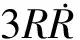
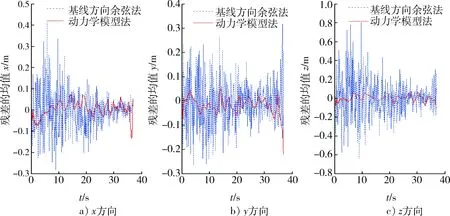
图2 位置分量残差的均值对比图Fig.2 Comparison chart of position residuals error mean

图3 速度分量残差的均值对比图Fig.3 Comparison chart of velocity residuals error mean

图4 位置分量的均方根误差对比图Fig.4 Comparison chart of position root-mean-square error

图5 速度分量的均方根误差对比图Fig.5 Comparison chart of velocity root-mean-square error

表1 均方根误差的均值Table 1 Mean of velocity root-mean-square error

方法名称Δx/mΔy/mΔz/mΔvx/(m·s-1)Δvy/(m·s-1)Δvz/(m·s-1)基线方向余弦法0.870 20.967 11.965 80.055 40.094 40.156 4动力学模型法 0.133 70.135 20.253 60.029 60.036 70.070 1

5 结束语

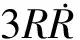
参考文献：

[1] 蔡洪．Unscented Kalman滤波用于再入飞行器跟踪[J]．飞行器测控学报，2003，22(3)：12-16．

CAI Hong．Unscented Kalman Filtering for Reentry Vehicle Tracking[J]．Journal of Spacecraft TT&C Technology，2003，22(3)：12-16．

[2] 蔡洪，张金槐．导弹飞行试验多站测量定轨的自适应滤波方法[J]．航天控制，1997(2)：17-22．

CAI Hong，ZHANG Jin-huai．Adaptive Filtering Approaeh for Missile Flight Test Trajectory Deterrulnation Under Multiple Station Measuring[J]．Aerospace Control，1997(2)：17-22．

[3] JULIER S J，UHLMANN J K．Unscented Filtering and Nonlinear Estimation[J]．Proc．IEEE，March 2004，92(3)：401-422．

[4] JULIER S J，UHLMANN J K，DURRANT-WHYTE H F．A New Method for Nonlinear Transformation of Means and Covariance in Filters and Estimators[J]．IEEE Trans．Automatic Control，Mar．1996，AC-45(3)：477-482．

[5] FARINA A，RISTIC B，BENVENUTI D． Tracking a Ballistic Target：Comparison of Several Nonlinear Filters[J].IEEE Transactions On Aerospace and Electronic Systems July 2002，38(3)：854-867．

[6] RISTIC B，FARINA A，BENVENUTI D． Tracking a Ballistic-Entry Object：Performance Bounds and Comparison of Non-Linear Filters[C]∥IDC-2002，Adelaide，Australia，February 2002：259-264．

[7] LI X R,JILKOV V P．A Survey of Maneuvering Target Tracking-Part II：Ballistic Target Models[C]∥2001 SPIE Conf on Signal and Data Processing of Small Targets，San Diego,CA,USA,July August 2001,Vol．4473：559-581．

[8] 杨炳尉. 标准大气参数的公式表示[J]. 宇航学报，1983,1(1)：83-86．

YANG Bing-wei．Formulization of Standard Atmospheric Parameters[J]. Journal of Astronautics，1983,1(1)：83-86．

[9] LI X R,JILKOV V P．A Survey of Maneuvering Target Tracking-Part Ⅲ：Measurement Models[C]∥2001 SPIE Conf on Signal and Data Processing of Small Targets，San Diego,CA,USA,July August 2001,4473： 423-446．

[10] 丁维福．多传感器信息融合理论及其在机动目标跟踪中的应用[D]．西安：西北工业大学，2007：19．

DING Wei-fu．Multi-Sensor Information Fusion Theory and Its Applications to Maneuvering Target Tracking[D]．Xi’an：Northwestern Polytechnical University，2007：19．

[11] WAN E A，MERWE R M．The Unscented Kalman Filter [M/OL]．(2001-08-01)[2009-04-03]http:∥stomach.v2.n1/docs-/TechPubs/Tracking_and_AR/wan01/unscented.pdf．

[12] 胡绍林，许爱华，郭小红．脉冲雷达跟踪测量数据处理技术[M]．北京：国防工业出版社，2007：120-135．

HU Shao-lin，XU Ai-hua，GUO Xiao-hong ．Pulse Radar Tracking Measurement Data Processing Technology[M]．Beijing：National Defence Industry Press，2007：120-135．