舰艇编队协同反导网络节点重要度评估*
2014-07-10夏昱滕克难陈健
夏昱,滕克难,陈健
(海军航空工程学院 a.研究生大队;b.训练部,山东 烟台 264001)
0 引言
研究表明[1-4]不同拓扑结构的网络对不同方式的攻击具有不同的抗毁性,在随机攻击下无标度网络比随机网络具有更强的容错性,但在选择性攻击下,无标度网络却又显得异常脆弱。因此,对复杂网络中节点的重要度进行评估是非常有意义的。由节点重要度评估找出那些重要的“核心节点”,可以通过重点保护这些“核心节点”提高整个网络的抗毁性和可靠性。
评估网络中节点重要性的方法很多,本质上都是源于图论[5-8],最简单的方法是以节点的连接度(节点连接的边数)作为节点重要度的衡量标准,认为与节点相连的边越多则该节点越重要[9]。这种评估方法具有片面性,有些重要的“核心节点”并不一定具有较大的连接度,比如只有2条边相连的“桥节点”[10]。文献[11-12]中提出的介数(betweenness centrality)能很好地衡量节点的重要度,即经过该节点的最短路径越多,该节点越重要,但仅仅用节点的介数表示节点重要度显然是不够全面的。文献[13]提出了一种基于生成树数目的节点删除法,定义最重要的节点为去掉该节点使得生成树数目最小的节点。节点删除法的问题是如果多个节点的删除都使得网络不连通,那么这些节点的重要度将是一致的,从而使得估计结果不精确。
本文首先定义了网络节点接近度和关联度,然后定义了节点的重要度。在此基础上给出了节点重要度评估方法及其算法,该方法结合了节点在复杂网路中的重要性,通过舰艇编队协同反导网络分析验证了该方法的有效性。
1 评估模型

1.1 节点介数
节点介数衡量了网络中所有的最短路径中经过该节点的数量比例,定义为
(1)
式中:σij(k)为节点i和j之间最短路径经过节点k的数目;σij为节点i和j之间最短路径的总数;V为网络节点集合。
节点介数体现的是网络中某个节点在整个网络传递信息过程中的重要程度,比如通信卫星映射的节点往往具有较高的点介数。节点介数的计算非常复杂,不仅要计算各个节点对之间的最短路径长度,还要记录这些最短路径的路线,为此利用Pajek软件计算节点的介数,它可以快速有效地计算出每个节点的介数。
1.2 节点接近度
假设d(vi,vj)表示以节点vi为起点,节点vj为终点的最短路径长度,则节点vi的节点接近度C(i)定义为
(2)
复杂网络本质上的非同质拓扑结构,决定了网络中每个节点的重要程度是不同的。节点在复杂网络中的重要度首先取决于节点在网络中的位置,根据式(2)可知,节点接近度C(i)越大,节点越居于网络中心,节点在全局网络中越重要。
1.3 节点关联度
灰色关联分析对系统数据序列几何关系和曲线几何形状的相似程度进行比较,以曲线间相似程度大小作为关联程度的衡量尺度。一组几何曲线形状越相似,则相应序列之间的关联度越大,反之则越小。由此为所考察的复杂系统综合决策提供信息。
节点关联度分析的基本思想是:首先确定复杂网络的“核心节点”,即认为与网络中所有节点均有边相连接的节点为最重要的“核心节点”,如星形网中的中心节点显然是网络中最重要的核心节点,可以通过重点保护这些“核心节点”提高整个网络的可靠性,也可以通过攻击这些“薄弱环节”,达到摧毁整个网络的目的。以此为基准,利用灰关联分析理论,用灰色关联度评价网络中各节点与理想节点的关联程度,通过对关联度进行排序,从而确定网络中的“核心节点”。
1.3.1 虚拟理想“核心节点”的确定
在复杂网络中,最理想的“核心节点”是与网络中每个节点都有边相连的节点,设其与每个节点的连接关系所构成的序列X0={X0(k)|k=1,2,…,n}(n为网络中的节点数)作为参考序列,比较序列为网络中每个节点与其余节点的连接关系所构成的序列:
Xi={Xi(k)|k=1,2,…,n},i=1,2,…,n,

1.3.2 关联系数的计算
关联系数是灰色关联分析中用于表示待评序列与参考序列接近程度的数值,值越大,表示接近程度越高,即越接近虚拟的理想“核心节点”,这样的节点即为网络中重要的“核心节点”。
比较序列Xi对于参考序列X0在k点的关联系数为
ξi(k)=
(3)
式中:ρ∈(0,+∞)为分辨系数。ρ越小,分辨能力越强,ρ∈(0,1) ,一般取ρ=0.5。
1.3.3 关联度计算
由于关联系数计算得到的是各比较序列与参考序列在各点的关联系数值,结果较多,信息过于分散,不便于比较,因此,须将每一比较序列各个时刻的关联系数集中体现在一个数值上,即关联度。通常关联度的计算方法采用平均值法:
(4)
式中:ξi(k)(i=1,2,…,n)为灰关联序列。
1.4 节点的重要度
1.4.1 节点重要度定义
为全面评价网络中节点的重要度,综合考虑节点的介数、接近度和关联度的影响,将节点vi的重要度定义为
(5)
K(i)越大,节点在网络中越重要。
1.4.2 节点重要度算法步骤
复杂网络中节点重要度评估的算法流程如下:
(1) 利用Pajek软件计算节点vi的介数B(i)。
(2) 计算节点vi的接近度C(i)。
1) 利用Matlab编程计算任意节点之间的最短路径长度;
2) 计算得到节点vi的平均最短路径长度;
3) 根据式(2)计算节点vi的接近度C(i)。
(3) 计算节点vi关联度A(i)
1) 选取参考序列X0={X0(k)=1|k=1,2,…,n,n为网络中的节点数};
2) 根据网络图得到比较序列,即图的邻接矩阵X=(Xi)n×n,Xi={Xi(k)|k=1,2,…,n},
i=1,2,…,n,k=1,2,…,n,
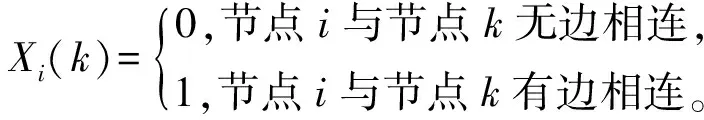
3) 根据式(3)计算比较序列Xi对于参考序列X0在k点的关联系数ξi(k);
4) 根据式(4)计算节点vi的关联度A(i)。
(4) 按照式(4)计算节点的重要度K(i),并将K(i)按从大到小排序,从而确定网络中每个节点的重要程度。
2 舰艇编队协同反导网络模型
2.1 模型仿真算例
假设有一个由10艘舰艇组成的舰艇编队,每艘舰艇的指控中心看成1个决策器D;舰艇上的导弹系统、前后主炮、深弹、火箭弹等武器装备及作战飞机、潜艇上的作战武器可以抽象为20个影响器I;舰艇上的雷达、声呐、光电传感器、参与作战的预警机、岸基观通站雷达和天基侦察卫星等抽象为20个传感器S;敌方发射5枚飞航式反舰导弹抽象为5个目标T。假设T,S,D,I4类节点的数目分别为NT,NS,ND,NI。这样,整个编队就能抽象为NT=5,NS=20,ND=10,NI=20的一个作战网络;各节点间连接概率为:PST=0.3,PDI=0.8,传感器S之间及影响器I之间的NW小世界网络中,加边概率PSS和PII分别取0.4和0.4,决策器D之间采用BA无标度网络进行连接。
这样整个舰艇编队协同反导作战网络的拓扑结构如图1所示。

图1 传感器之间和影响器之间采用NW小世界网络连接且决策器之间BA无标度网络连接的舰艇编队协同反导网络拓扑结构图Fig.1 Formation of antimissile network of which sensors and influencers use NW small-world and decision-making uses BA free-scale network
2.2 模型参数分析
传感器之间和影响器之间采用NW小世界网络连接,决策器之间采用BA无标度网络连接构建的舰艇编队反导作战网络,利用Pajek软件得到该网络模型的特征参数如表1所示。模型各节点的度分布如图2所示,其中节点1~5为目标节点,节点6~25为传感器节点,节点26~35为决策器节点,节点36~55为影响器节点。
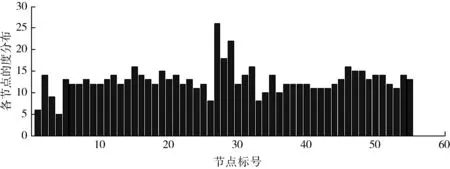
图2 舰艇编队协同反导网络的度分布图Fig.2 Degree distribution of fleet cooperation antimissile network
3 舰艇编队协同反导网络节点重要度评估
根据1.4.2节中网络节点重要度评估的算法流程,计算舰艇编队协同反导网络中所有55个节点的重要度。表2给出了所有节点的重要度评估结果。

表1 舰艇编队协同反导网络模型参数Table 1 Model parameters of fleet cooperation antimissile network
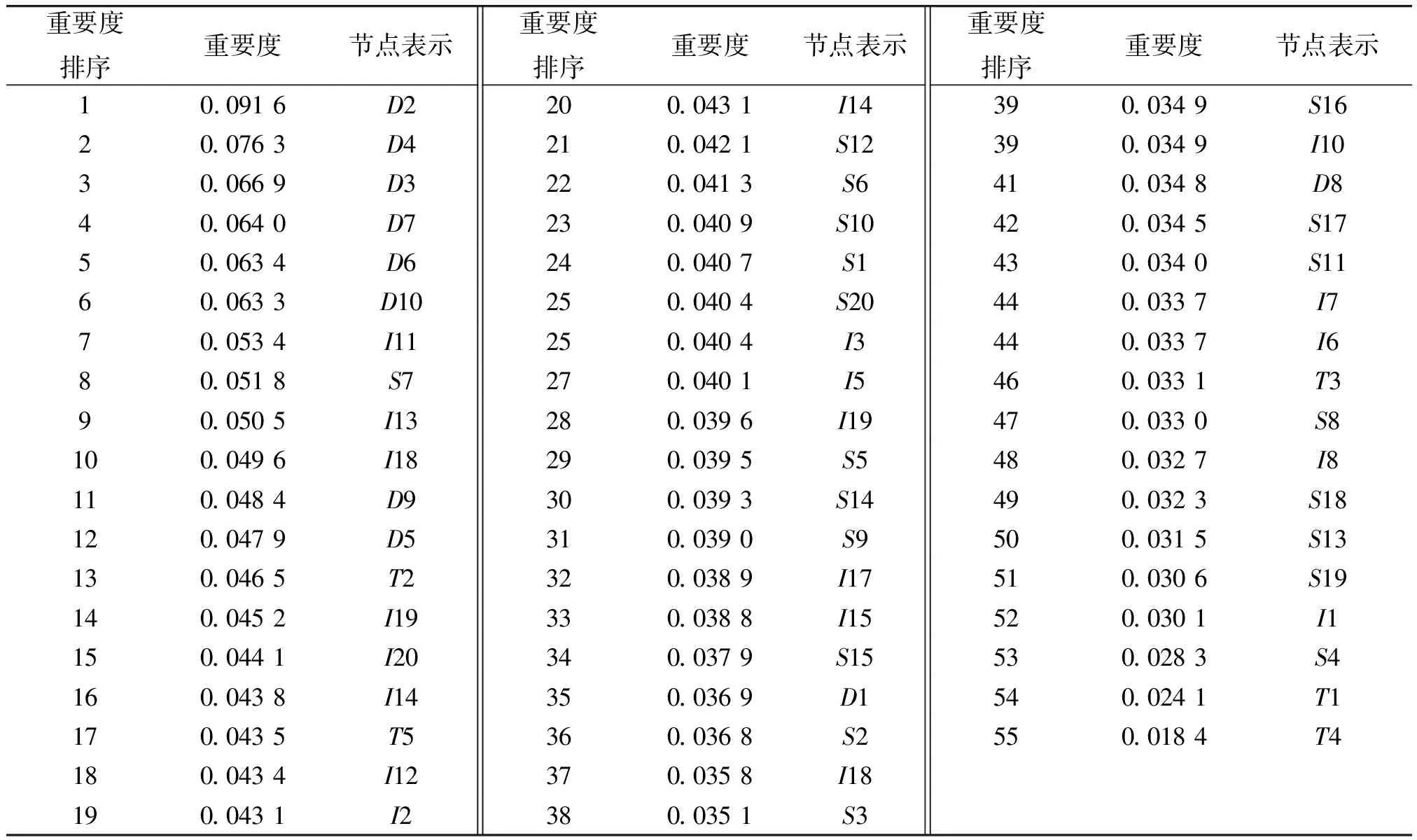
表2 舰艇编队协同反导网络重要度评估结果
通过表2舰艇编队协同反导网络重要度评估结果,可以看出,决策器D是网络中最重要的节点,这正与其在舰艇编队协同反导网络中的作用相匹配;其次重要的节点为影响器I,由于影响器I与决策器D、目标T及I之间的互连,使得影响器I的度增加,因而其重要性增加;虽然传感器S与影响器I的网络都采用了小世界网络互连,但由于舰艇编队反导网络为有向边网络,存在从目标T到传感器S和从影响器I到目标T的连接,因此,影响器节点的出度要大于传感器节点的出度,因而具更大的重要度。
4 结束语
本文中针对有向网络提出了基于节点接近度及关联度评估节点在复杂网络中的重要度方法,定义了节点的接近度、关联度及重要度,全面综合地描述了节点在复杂网络中的重要性,针对舰艇编队协同反导网络中节点的重要度,证明了该方法的有效性。
参考文献:
[1] 丁琳, 谭敏生, 肖炜. 复杂网络抗毁性研究综述[J]. 网络通讯及安全, 2009, 5(1): 51-61.
DING Lin, TAN Min-sheng, XIAO Wei. Reaserch Summarize About Anti-Destroying of Complex Network[J].Network Communication an Safe,2009,5(1):51-61.
[2] 谭跃进, 吴俊, 邓宏钟, 等. 复杂网络抗毁性研究综述[J]. 系统工程, 2006, 24(10): 1-5.
TAN Yue-jing, WU Jun, DENG Hong-zhong,et al. Reaserch Summarize About Anti-Destroying of Complex Network[J]. System Engineering,2006, 24(10): 1-5.
[3] 潘丽君,范锐,王精业.基于作战仿真的军用通信网络战时抗毁性研究[J].计算机工程,2010,6(5):4-7.
PAN Li-jun,FAN Rui,WANG Jing-ye. Wartime Anti-Destroying Ability Based on Combat Simulation of Military Communication Network Research[J]. Computer Engineering,2010,6(5):4-7.
[4] 张琨,谈革新,庄克琛.复杂网络抗毁性测度研究综述[J]. 计算机时代,2006,32(22):111-113.
ZHANG Kun,TAN Ge-xin,ZHUANG Ke-chen.Reaserch Summarize Network About Anti-Destroying of Complex Network[J].Computer Time,2006,32(22):111-113.
[5] 谭跃进, 吴俊, 邓宏钟.复杂网络中节点重要度评估的节点收缩方法[J].系统工程理论与实践, 2006,11(11):79-83.
TAN Yue-jin,WU Jun,DENG Hong-zhong. Shrinkage Method for Node Important Degree Evaluation of Complex Network[J]. Systems Engineering Theory and Practice, 2006, 11(11):79-83.
[6] 张翼,刘玉华,许凯华,等.一种基于互信息的复杂网络节点重要性评估方法[J].计算机科学,2011,38(6):88-89.
ZHANG Yi,LIU Yu-hua,XU Kai-hua,et al.A Kind of Complex Network Node Importance Evaluation Method Based on Mutual Information[J]. Computer Science,2011, 38(6):88-89.
[7] ENRICO N, GUIDO P, PETER W Finding the Most Vital Node of a Shortest Path [J].The Oretical Computer Science,2003,29(6):278-287.
[8] 邱原,邢焕革.基于复杂理论的作战网络关键边评估方法[J].兵工自动化,2011,30(8):22-26.
QIU Yuan,XIN Huan-Ge. Operational Key-Edge Network Evaluation Method Based on the Theory of the Complex[J]. Weapons Industry and Automation, 2011,30(8):22-26.
[9] WEST D B. Introduction to Graph Theory[M].Englewood Cliffs: Prentice Hall, 2001.
[10] CALLAWAYDS, NEWMANMEJ, STROGATEZSH, et al. Network Robustness and Fragility: Percolation on Random Graphs[J] . Phys. Rev. Lett., 2000, 85(25): 5468-5471.
[11] 陈静, 孙林夫.复杂网络中节点重要度评估[J]. 西南交通大学学报, 2009, 44(3): 426-429.
CHEN Jing,SUN Lin-fu. The Evluation of Important Degree about Nodes in Complex Network[J]. Journal of Southwest Jiaotong University, 2009, 44(3): 426-429.
[12] FREEMAN L C. A set of Measures of Centrality Based upon Betweenness[J]. Sociometry, 1977, 40(1): 35-41.
[13] 陈勇,胡爱群,胡俊,等. 通信网络中最重要节点确定方法[J]. 高技术通讯, 2004(1): 573-575.
CHEN Yong,HU Ai-qun,HU Jun, et al. The Determine Method of the Most Important Node in Communication Network[J].High Technology Commution, 2004(1): 573-575.
