基于协方差分析的一种改进比例制导律研究*
2014-07-10冯德龙杨锁昌刘映希
冯德龙,杨锁昌,刘映希
(1.军械工程学院 导弹工程系,河北 石家庄 050003;2.西安电子科技大学 雷达信号处理实验室,陕西 西安 710071)
0 引言
导弹制导系统是一个具有随机输入的非线性时变系统,在此系统中含有非线性因素和一些随机效应,这些非线性因素和随机效应影响导弹制导精度。对具有随机输入的非线性时变系统进行统计分析,传统的方法是采用Monte Carlo方法。但由于此方法存在计算量大、耗时过长的缺点,使得在一些对快速性能要求较高的环境无法使用该方法。协方差分析描述函数技术(covariance analysis describing equation technique,CADET)是在20世纪70年代由美国人A.Celb和R.S.Warren共同提出的对战术飞行器制导系统性能进行统计分析的一种新方法。它解决了Monte Carlo方法快速性能较差的缺点[1]。协方差分析是一种用于分析具有随机输入的时变线性系统的计算机工具。应用这种方法,通过对非线性矩阵微分方程式进行直接积分,就可以产生作为一个时间函数的系统状态向量协方差矩阵。应用这种技术,可以预估导弹制导系统的统计特性[2-4]。
1 CADET技术
1.1 协方差分析描述函数技术的基本原理
假设具有随机输入的连续非线性系统状态方程为[5]
(1)
式中:f(x,t)为n维系统状态变量x(t)的非线性向量函数。非线性时变系统方程如图1所示。
图1 非线性时变系统方程示意图Fig.1 Schematic diagram of nonlinear time-varying system
非线性系统的传播方程:

GT(t).
(2)
定义辅助矩阵N,使得
NP(t)=Ef(x,t)rT,
(3)
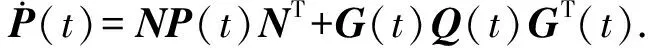
(4)
由于P(t)是正定的,故有
N=Ef(x,t)rTP-1.
(5)
根据上述统计线性化原理,令非线性函数向量f(x,t)可近似描述为x(t)的一个线性函数:
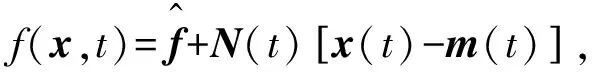
(6)
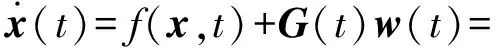
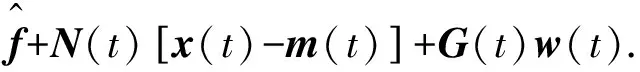
(7)
非线性时变系统均值方程和协方差传播方程为
(8)
初始条件同上,利用方程(8)和初始条件式可直接解算系统变量的误差统计特性。
1.2 高斯假设
目前,大多数协方差描述函数技术的研究都是采用假定系统状态变量为高斯分布的办法[6-7]。
(1) 高斯假设的重要结论
1)设系统的状态变量都是正态的,则矢量非线性函数f(x,t)中的每一个标量非线性函数都可以单独进行准线性化。
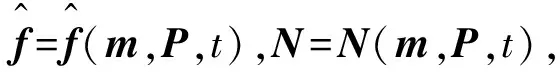
(9)
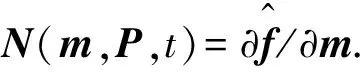
(10)
(2) 高斯假设的合理性
高斯分布的随机过程通过非线性系统,其输出量就变成非高斯分布的了[8]。即使这样,高斯假设在工程上仍有它的实用价值,原因在于导弹制导系统的线性部分通常都具有较好的低通滤波作用。由中心极限定理可知,非高斯分布的随机过程通过低通滤波后,将趋向于高斯随机过程。由于系统线性部分的滤波作用,使得高斯假设基本成立。
(3) 根据上述理论假设[9]
1)x(t)服从联合正态分布。
2) 非线性的随机干扰以线性方式加入到系统当中,且服从正态分布。
2 一种改进比例制导律精度分析
2.1 制导回路模型
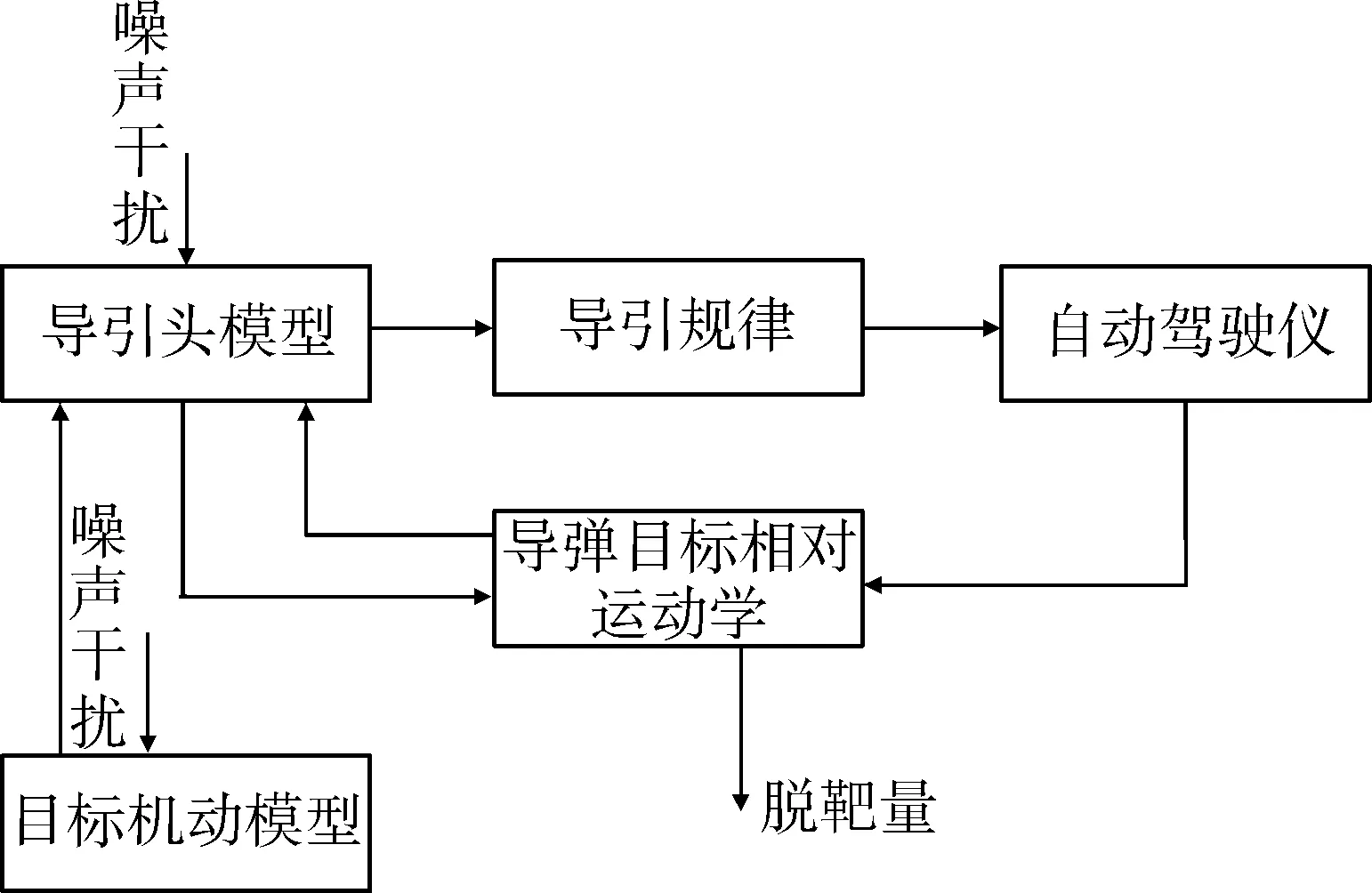
图2 制导回路模型Fig.2 Guidance loop model
导弹自寻的末制导回路模型包括自动驾驶仪模型、导引头模型、导弹目标相对运动模型、制导律和目标机动模型[10-11],其相互关系如图2所示。
2.2 制导律
本文对一种改进的比例导引律进行分析,其形式如下:
(11)
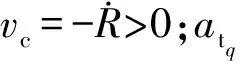
2.3 协方差分析

后面几个字起了作用,花五奇这些年作为德公公贴身护卫,早已习惯眉高眼低看人,老太医往往品级不低,且能与后宫说上话,轻易不能得罪,于是他暂时放下兵器,不耐烦地问道:“老太医?什么老太医?”
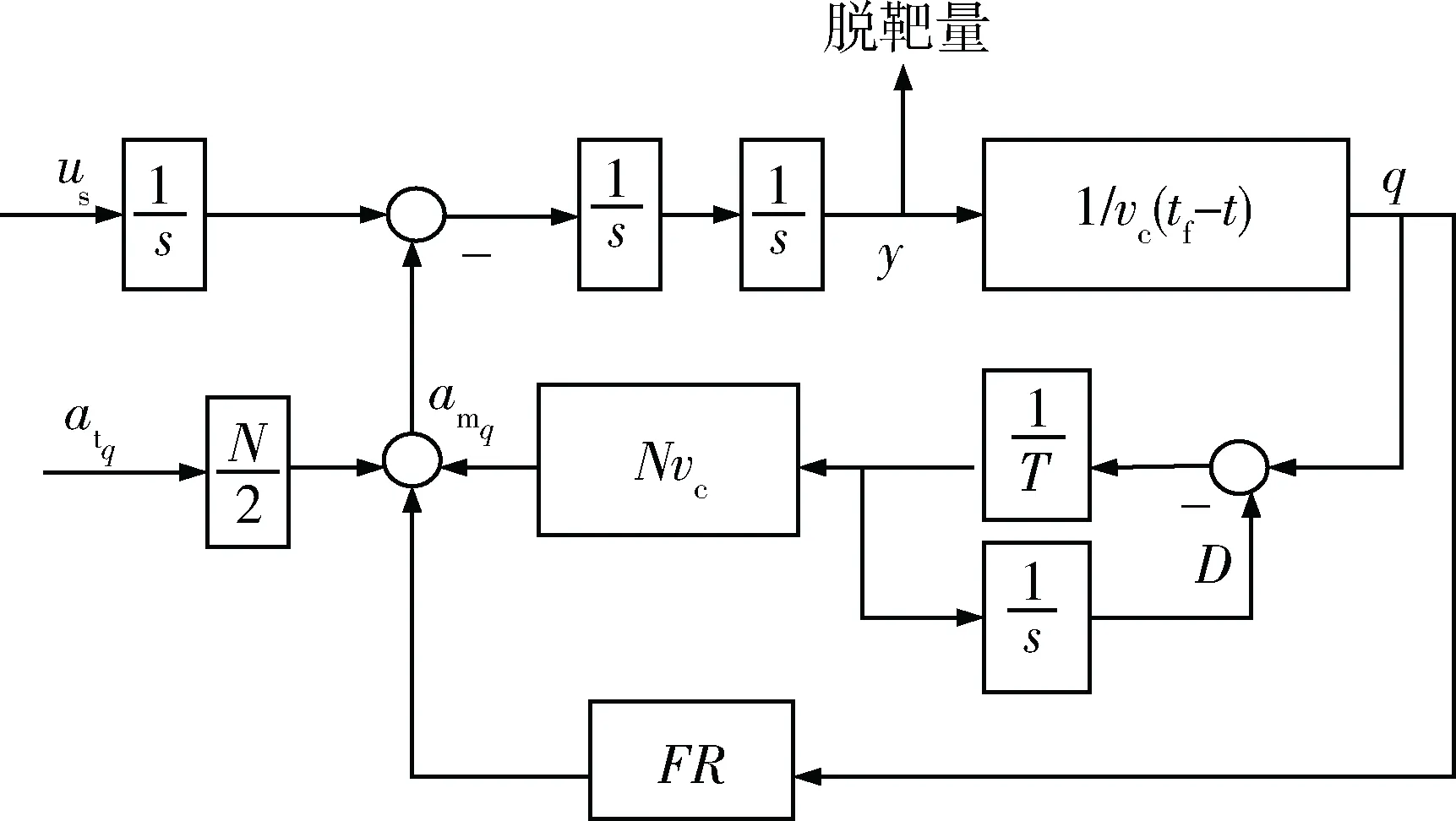
图3 制导回路Fig.3 Guidance loop

(12)
式中:
(13)
因为上述一阶微分方程式是状态的函数,它们可以写成状态空间表达如下:
(14)
定义:
则系统状态方程可以表述为
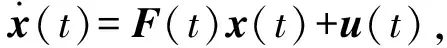
(15)
式中:x(t)为系统的状态;F(t)为系统动态特性矩阵;u(t)为具有谱密度矩阵Q(t)的白噪声矢量,即
Q(t)=Eu(t)uT(t),
(16)
(17)
其中协方差矩阵X(t)与x(t)的关系为
X(t)=Ex(t)xT(t).
(18)
如果随机干扰具有零均值,则协方差矩阵的对角元素表示状态变量的方差。协方差矩阵的非对角元素表示状态变量之间的相关程度。
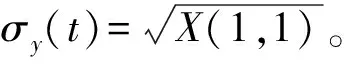
3 仿真分析
3.1 程序仿真
整个仿真程序都是采用Matlab编写,仿真的流程图如图4所示。
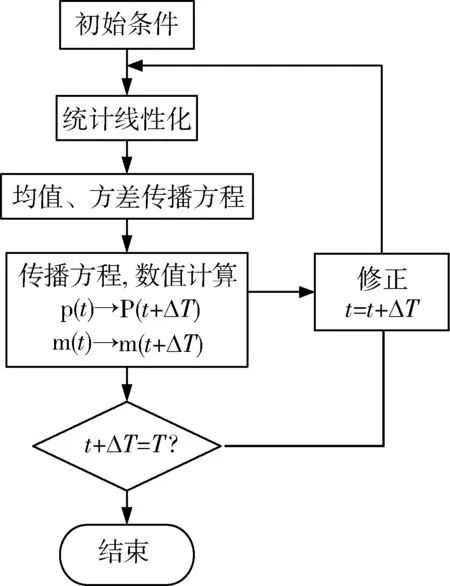
图4 CADET仿真流程图Fig.4 Flow chart of CADET simulation
根据图4所示的线性化末制导模型,导弹飞控系统为一阶惯性环节且时间常数T为1 s,飞行时间tf为0~10 s,有效导航比为3,比例系数F为0.5,弹目相对速度为4 000 m/s,目标的加速度为5 m/s2。在制导系统中唯一的误差源是目标机动特性为3g的阶跃机动且开始时刻在整个飞行时间内均匀分布。仿真结果如图5~8所示。

图5 比例导引律的协方差分析Fig.5 Covariance analysis of proportional guidance law

图6 改进比例导引律的协方差分析Fig.6 Covariance analysis of improved proportional guidance law
图7 比例导引律的导弹加速度变化Fig.7 Missile acceleration change of proportional guidance law

图8 改进比例导引律的导弹加速度变化Fig.8 Missile acceleration change of improved proportional guidance law
3.2 结果分析
如图8所示是整个飞行时间为10 s时,导弹与目标的相对距离的总的标准差。由图5和图6可以看出这种改进的比例导引律比之前的导引精度提高了大约3倍,所以这种改进是有效的、可行的。与伴随技术不同,协方差分析方法在一次仿真中并不能提供所有不同飞行时间的脱靶量,但协方差分析方法可以得到在一次飞行时间内所有时刻的相对距离y的信息,在飞行结束时,相对距离即为脱靶量,即σmiss=σy(tf),而且也可以得到图7和图8所示的导弹加速度变化。
4 结束语
协方差分析描述函数技术是非线性时变系统统计分析的一种近似解析方法,它可以通过一次解析计算得到系统所有状态变量的统计性能。该方法较传统的蒙特卡罗试验法要节省很多计算时间。本文对于一种改进的比例导引律,应用协方差分析法验证了其可行性。协方差分析方法虽然也适用于分析随机干扰的影响,但是只能获得飞行末端时刻的脱靶量,对各干扰的影响需进行独立仿真。
参考文献:
[1] 毕开波,王晓东,刘智平.飞行器制导与控制及其MATLAB仿真技术[M].北京:国防工业出版社,2009:163-169.
BI Kai-bo, WANG Xiao-dong, LIU Zhi-ping. Vehicle Guidance and Control and Matlab Simulation [M]. Beijing: National Defense Industry Press, 2009:163-169.
[2] 郭庆,杨明,王子才.拦截器末制导段误差模型的建立与仿真[J].计算机仿真,2007,24(3):58-61.
GUO Qing, YANG Ming, WANG Zi-cai. Establishment and Simulation of Error Model for Interceptor’s Terminal Guidace Phase [J]. Computer Simulation, 2007, 24(3): 58-61.
[3] 蒋瑞民,周军,郭建国. 导弹制导系统精度分析方法研究[J].计算机仿真,2011,28(5):76-79.
JIANG Rui-min, ZHOU Jun, GUO Jian-guo. Research on Methods of Missile Guidace Precision Analysis [J]. Computer Simulation, 2011, 28(5): 76-79.
[4] 柴华,杏建军,唐国军.基于协方差分析描述函数技术的弹道导弹落点预报[J].导弹与航天运载技术,2011,4(4):37-40.
CHAI Hua, XING Jian-jun, TANG Guo-jun. Ballistic Missile Impact Poit Prediction Based on CADET [J]. Missile and Space Vehicles, 2011, 4(4): 37-40.
[5] 周卫文,梁晓庚,贾晓洪.自寻的导弹末制导系统仿真分析方法研究[J].计算机仿真,2012,29(8):45-49.
ZHOU Wei-wen, LIANG Xiao-geng, JIA Xiao-hong. Study on Missile Homing Loop Performance Analysis Methods [J]. Computer Simulation, 2012, 29(8):45-49.
[6] YANUSHEVSKY R.Analysis and Design of Missile Guidance Systems in Frequency Domain [C]∥ 44th AIAA Space Sciences Meeting, Reno,Nevada,2006:821-825.
[7] SHNEYDOR N A.Missile Guidance and Pursuit[M].Chichester:Horwood Publishing,1998.
[8] WANG Z M.A New Method for Estimating System Error of Guidance Instrument [J]. Science of China:Series E, 1998, 28(2): 160-167.
[9] 李海平,钟瑞麟,魏岳,等.导弹末制导精度分析的协方差方法研究[J].战术导弹技术,2004,6(1):49-54.
LI Hai-ping, ZHONG Rui-lin, WEI Yue, et al. Research on Covariance Method of Accuracy Analysis in Missile Terminal Guidance [J]. Tactical Missile Technology, 2004, 6(1): 49-54.
[10] XU Jin-xiang. Key Techniques of Terminal Correction Mortar Projectiles [J]. Journal of Beijing Institute of Technology, 2007, 16(2):168-172.
[11] FRORIEP R, JOOST D. Stocchastic Simulation Using Covarince Techniques: Modular Program Package for Nonlinear Missile Guidance [J]. Journal of Guidance and Control, 1984, 7(4): 509-512.
[12] Iain Matthews, Takahiro Ishikawa, Simon Baker. The Template Update Problem [C]∥IEEE Transactions on Pattern Analysis and Machine Intelligence, 2004, 6(6): 810-815.
