基于selfGDE3算法的低轨预警系统优化设计方法*
2014-07-10简平邹鹏熊伟
简平,邹鹏,熊伟
(装备学院a.研究生管理大队;b.重点实验室,北京 101416)
0 引言
为应对未来战争弹道导弹不断增加的威胁,及时的预警和有效的跟踪越来越重要。与地基、海基、空基预警相比,天基预警系统不受地球曲率的限制,通过星载红外探测器尽早探测到弹道导弹的发射,并将信息迅速传递给地面中心,能够提供更加广阔的更长的预警时间和监视范围,以组织有效的反击。红外低轨预警系统通过多星协同工作对自由段导弹目标进行捕获与跟踪,针对低轨预警系统的设计日益受到广泛关注。天基低轨预警系统设计,是一个多目标优化问题,要从天基传感器的特点和系统任务的要求两方面出发,设计目标是在现有的经济条件下尽量提高系统的覆盖性能和监视能力。国内外对低轨星座系统设计已经开展了很多研究,近年来对红外低轨星座系统也有一些涉足。文献[1]利用改进的低轨道星座设计方法,研究了以最少的卫星来实现空间一重覆盖问题。文献[2-3]探讨了多学科协同优化的红外低轨星座设计方法。文献[4-5]提出了描述空间观测性能指标和基于纬度威胁加权的观测性能评估方法,并考虑星座成本及碰撞因素,建立了星座优化目标函数,引入GDE3(generalized differential evolution 3)算法对红外低轨星座进行了优化设计。以上研究有的只考虑星座对地面的覆盖特性,不能优化星座构型,有的对星座构型中的离散变量(如卫星数、轨道面数目)的优化设计考虑不全面,有的没有考虑GDE3算法本身性能因素,从而影响了系统优化设计的效果。本文在以上研究的基础上,从影响GED3算法性能的控制参数着手,研究了自适应控制参数的优化设计方法,建立了低轨预警系统优化指标模型,设计了系统优化的目标函数,最后进行了仿真实验。
1 自适应通用差异演化算法
近些年来,人们通过模拟自然界生态系统机制,提出了一系列求解复杂优化问题的仿生优化算法,如遗传算法、蚁群算法、粒子群算法、差异演化算法等,以及S.Kukkonen和Jouni Lampinen等先后提出三代通用差异演化算法[6-8],为解决低轨预警系统多目标优化设计提供了思路。
1.1 通用差异演化算法原理
差异演化算法是一种基于种群演化的实数编码,可以隐并行地搜索解空间的多个解,产生基于Pareto最优概念的多目标优化的演化算法。通用差异演化算法[6-9]共发展了3代,GDE3[9]对原有的GDE和GDE2进行了改进,将DE方法应用到具有M个目标函数和V个约束函数的问题。GDE3算法的基本流程:
(1) 输入初始化参数D,Gmax,NP≥4,F∈(0,1+],初始基向量:xlo,xhi。

(3) 交叉变异产生父代个体的试验个体。任意选择r1,r2,r3∈{1,2,…,NP}用来生成xj, i,G的试验个体,其中r1,r2,r3与i两两互异,并产生随机参数jrand=rand(1,D)。则试验个体uj, i,G的每个决策变量有
for(j=1;j≤D;j=j+1)
{
if(randj[0,1) uj,i,G=xj,r3,G+F(xj,r2,G-xj,r1,G) else uj,i,G=xj,i,G } (1) CR控制交叉操作,代表试验个体选择3个父代个体线性组合的概率;F控制问题解的搜索速度和鲁棒性。采用这种交叉策略可以确保下一代个体中至少1个染色体来源于试验个体uj,i,G。 (4) 选择操作。对于2个不可行解,选择试验个体和父代个体中占优的解,如果互不占优,则选择父代个体;对于可行解和不可行解,选择可行的个体;如果试验个体和父代个体均可行,选择占优的解,如果互不占优,同时选择2个解,且m=m+1。 (5)i=i+1,如果i (6) 非劣排序。选择合适个体,保持G+1代种群规模为NP。对G+1代的种群PG+1={x1,G+1,x2,G+1,…,xNP,G+1,…,xNP+m,G+1}(规模为NP到2NP之间),通过非劣排序和计算拥挤距离的方法,使得种群规模为NP。 (7) 若G (8) 输出当前种群即为Pareto最优解。 控制参数对差异演化算法的优化能力和收敛速度等性能会产生较大的影响。在通用差异演化算法中主要有3个控制参数:种群规模NP,缩放因子F和交叉概率CR。这3个参数是保持不变的,要获得最优的参数设置比较困难,因此,有学者提出了自适应调整控制参数的策略[10],在演化过程中F和CR以概率的形式随种群发生变化,但未考虑个体的适应度和多目标的情况,具有一定的盲目性。相对于NP,差异演化算法的性能对F和CR更敏感[11],自适应技术主要应用于F和CR参数。当利用当前的F和CR产生的新个体的适应度优于父代个体时,说明这2个参数是合适的,则无需对这2个参数进行调整,基于这种思想并借鉴单目标优化自适应参数控制方法,将个体的适应度作为参数调整的依据,并结合一定的调整概率提出一种新的对F和CR参数自适应控制策略,提高算法的搜索能力。在调整过程中加入了适应度的比较,目标是让缩放因子向当前种群中较好的参数方向取值。具体方法是:对种群个体采用不同的F和CR,在演化过程中则按如下公式自动调整(以最小化目标函数为例): (2) (3) 式中:randk,k∈1,2,3,4为[0,1]区间的随机数;Fbest,G为当前种群中非劣排序后第1个体对应的缩放因子;ui,Gxi,G表示试验个体劣于(非支配)父代个体。 从式(3)和(4)可以看出,如果个体i用其对应的Fi和CRi值生成的新个体的适应度优于该个体当前适应度,则表明该个体的缩放因子和交叉概率取值是有效的,保留该缩放因子和交叉概率到下一代。只有在ui,G的适应度劣于xi,G的适应度值,并且随机数小于调整概率τ1,τ2时,才生成新的缩放因子和交叉概率。α是向Fbest,G的趋向率,可表示为 (4) 式中:fj(xbest,G)为当前种群中非劣排序后第一的个体对应的第j个目标适应值;M为优化目标数。 随着个体xi,G与种群最优个体几何平均距离的增加,其对应参数Fi,G+1向Fbest,G的趋向率α也越大,相应的随机扰动越小;当个体xi,G与最优个体接近时,其对应参数的随机扰动就会增加。参数的自适应控制使种群中适应度较差的个体向着种群中的最优个体趋近,提高算法的性能。自适应控制参数的通用差异演化算法(gencralized differential evolution algorithm self-controlled,selfGDE3)的描述如下: (1) 设定种群规模NP,最大演化代数Gmax及τ1,τ2的值; (2) 随机初始化种群及种群中每个个体对应的参数Fi和CRi,G=0; (3)i=0; (4) 利用个体xi(t)对应的参数Fi和CRi,按照GDE3算法的工作策略执行变异、交叉和选择操作,生成新一代个体xi,G+1; (5) 按照式(4)计算趋向率α; (6) 按照式(2)和式(3)更新个体xi,G+1对应的Fi,G+1,CRi ,G+1; (7)i=i+1; (8) 如果i (9) 通过快速非劣排序保持种群规模为NP; (10) 如果G (11) 输出当前种群即为Pareto最优解。 凝视传感器探测视场对关注空域的覆盖性能反映了低轨星座对深空背景目标的探测能力。根据所需分析圆球面Λn的半径Rn与卫星轨道半径Rs和最小指向角时的工作切线半径Rm的位置关系不同,对应的空间覆盖范围也不同[12]。根据图1分析目标的覆盖情况: 图1 覆盖分析示意图Fig.1 Picture of coverage analysis (4) 当目标所处的圆球面Λn的半径Rn在传感器的最小指向角切线高度以内时,即OH≤Rn≤Re,Re为地球半径。由于球面Λn不在卫星S传感器的视线范围内,因此目标不能被卫星S覆盖和探测。 在优化设计中以平均N重几何覆盖面积百分比CovNg为覆盖优化目标: (5) 式中:T为时间周期推进时间点数;Ssum为被分析空间区域的面积;P为其点区域总数。 以Sj表示某一点区域j的面积,点区域特征点被覆盖即认为该点区域被覆盖,kij表示某一时刻i对点区域的覆盖重数。由于2颗卫星即能对目标形成立体观测,本文选取N为2,并在优化过程中采用网格点仿真方法求取覆盖优化指标。 在低轨红外预警系统中,需要2颗或以上卫星对目标进行定位,简化描述目标与卫星几何关系对跟踪精度的影响,可将其几何关系转化到二维平面内,定位系统可抽象为一个只测角定位系统,从每颗卫星获得两维像平面观测[13]。通常使用GDOP度量描述预警卫星对目标的定位误差。GDOP定义如下: (6) (7) (8) 式中:Pθ为目标的定位误差协方差矩阵;θ1和θ2为2个卫星分别测得目标的观测角。 GDOP越小精度越高。在优化设计中以平均定位精度GDOPavg为优化目标: (9) 式中:T为时间周期推进时间点数;P为某一时间点区域总数;Psum为T和P的乘积。GDOPi,j为i时间点j网格区域的定位精度,如果系统对目标的覆盖在2重以上,需要两两计算卫星对目标的定位精度取最小值作为GDOPi,j值。 卫星数量是影响星座成本的主要因素,在卫星数目一定的情况下,轨道面数越少成本越低,轨道高度越低轨道倾角越低,则所需的发射能量越小,成本也随之减少。单星成本估算主要考虑其制造、发射和保险成本,这3方面与卫星质量、轨道高度密切相关。卫星星座成本(以Ccons表示,亿美元)估算如下[5]: (10) 式中:β为保险费所占比例,一般为0.2;h为卫星轨道高度,km;λ1,λ2和λ3为权重因子,λ1+λ2+λ3=1;P为轨道面数;N为星座卫星配置数量;i为卫星轨道倾角,(°);ih和i1为轨道倾角的上下限值。 采用基于selfGDE3算法对天基低轨预警星座系统设计,在仿真时间内对覆盖性能、定位精度和星座成本设计目标的计算值为个体的3个适应度,作为进化个体的一部分。下面就低轨预警星座系统个体编码、优化设计相关问题进行实例分析。 本模型的决策变量代表星座系统参数的选择。Walker星座具有良好的全球覆盖特性,对于红外低轨系统,一般采用的星座构型为Walker星座,星座由7个要素确定:卫星数量(S),轨道面数(P),谐参数(F),轨道高度(h),轨道倾角(I),第一轨道面升交点赤经(Ω0),第一轨道面第1颗卫星初始时刻纬度幅角(u0)。Walker星座中第i轨道面上第j颗卫星的升交点赤经Ωi,j和纬度幅角ui,j就可表示为 (11) (12) 运用selfGDE3算法进行优化设计时,有如下特殊情况需要说明: (1) 离散型变量的编码问题 由于星座系统优化设计的变量S,P和F属于离散型的整数,因此在对这几个变量的交叉变异后需要取整数,保证卫星数量(S)能够整除轨道面数(P),如果S不能整除P,则 S=S+P-mod(S,P) . (13) (2) 趋向率问题 由于在低轨预警系统优化设计中的有关覆盖率优化目标为:1-CovNg,取最小值,如果覆盖率达到100%,f1(xbest,G)趋近于0,因此趋向率式(4)中求和的分母接近0,程序中无法计算,因此针对预警系统的覆盖优化目标将趋向率改为 (14) 地球模型为圆模型,红外感器探测距离范围为0~7 000 km,俯仰方向光轴指向范围为-180°~180°,水平方位光轴指向方位为-90°~90°,引入的测角误差为80 μrad,λ1,λ2和λ3分别为0.5,0.4和0.1,观测空间:高度范围20~600 km;纬度范围为-30°~30°;经度范围为-180°~180°,selfGDE3算法参数CR和F为0.8,调整概率τ1和τ2取0.9,种群规模为50,进化代数100。 在本文的仿真参数条件下,采用selfGDE3算法进行仿真实验,得到多种优化方案及性能指标,如表1中的1~10方案。 表1 星座系统方案Table 1 Data of preliminary constellations 其中表中的方案a为文献[5]采用GDE3优化设计方法得出的较佳系统星座方案,方案b是文献[2]采用多学科优化设计方法得出的最佳星座系统方案,方案中的性能指标值是根据本文的优化模型求得的。根据不同的考虑侧重因素,可以初步选择不同目标相对较好的不同星座系统方案,如果关注点较为分散(不是特定某一优化目标),在最终选择方案时需要综合考虑各个因素,选择一个使各个目标都较优的综合性的方案。一种基于理想点的方法[14]可用来处理这种情况下的多目标方案选择的决策问题。本文选择方案6作为最优星座。 本文选择方案6与方案b进行星座系统性能仿真对比分析(在仿真中,方案b的Ω0,u0参数是随机产生)。在本文的仿真条件下,与方案b相比,方案6的平均二重覆盖百分比高1.1%,平均定位精度值小159.752 m,星座成本少0.61亿美元,针对不同高度,2个方案的二重覆盖率对比如图2所示。方案6在高度260 km左右达到100%二重覆盖率,而方案b在310 km左右才达到100%二重覆盖率,在此高度之前,方案6的二重覆盖率都比方案b高。2个方案的定位精度随高度变化的对比如图3所示。方案6在不同高度下定位精度值都低于方案b的值,定位效果明显好于方案b。 图2 方案6和b二重覆盖随高度变化对比图Fig.2 Comparison of 2-cover by altitude to scheme 6 and b 图3 方案6和b平均定位精度随高度变化对比图Fig.3 Comparison of positioning precision by altitude to scheme 6 and b 通过以上的仿真分析可以看出,本文方法设计的方案6的性能整体优于方案b,验证了selfGDE3优化设计方法的有效性。对于2个非支配方案解6和7,如果考虑覆盖率和成本,选择方案7更合适,否则可以选择方案6。 本文提出了自适应控制参数的差异演化算法,建立了低轨预警系统优化设计的空间覆盖模型、定位精度模型和星座成本计算模型,确定了优化设计中具体的编码方案和遗传操作算子,解决了低轨预警星座系统设计中的离散变量选取、优化参数自适应控制的问题。通过仿真可以得出低轨星座方案,并通过性能仿真验证了本文所研究的优化设计方法的有效性和优越性。本文所建立的低轨预警系统的优化模型、提出的基于selfGDE3的系统优化设计方法可为红外低轨预警星座系统研究提供方法基础和参考,为进一步开展天基低轨预警系统应用研究(如面向导弹跟踪的天基预警系统任务规划和传感器资源调度研究)奠定基础。 参考文献: [1] JOHN M H, ALEXANDER N, Linden. Improved Low-Altitude Constellation Design Methods[J]. American Institute of Aeronautics and Astronautics, 1989,12(2):228-236. [2] BUDIANTO I A,OLDS J R, A Collaborative Optimization Approach to Design and Deployment of a Space Based Infrared System Constellation[C]∥IEEE Aerospace Conference Proceedings.Montana,2000:18-25. [3] BUDIANTO I A,OLDS J R. Design and Deployment of a Satellite Constellation Using Collaborative Optimization[J].Joural of Spacecraft and Rockets, 2004,41(6):956-963. [4] 邓勇,王春明,胡晓惠. 基于空间纬度区域优化的红外近地轨道星座设计[J].宇航学报,2010,31(5): 1368-1373. DEND Yong,WANG Chun-ming,HU Xiao-hui.A Spatial Latitudinal Region Optimization-Based Infrared LEO Constellation Design[J]. Journal of Astronautics, 2010,31(5): 1368-1372. [5] 王春明,陈曦,邓勇.基于GDE3算法的红外低轨星座设计[J]. 北京航空航天大学学报,2010, 36(7):857-861. WANG Chun-ming,CHEN Xi, DEND Yong.Infrared LEO Constellation Design by GDE3 Algorithm[J].Journal of Beijing University of Aeronautics and Astronautics, 2010,36(7):857-861. [6] LAMPINEN J.DE’s Selection Rule for Multi-Objective Optimization[EB/OL].(2012-05-06)[2012-07-11].http:∥www.it.lut.?/kurssit/ 03- 04 / 010778000/MODE.pdf. [7] KUKKONEN S, LAMPINEN J. An Extension of Generalized Differential Evolution for Multi-Objective Optimization with Constraints [C]∥ Proceedings of the 8th International Conference on Parallel Problem Solving from Nature (PPSN VIII), Birmingham, England, 2004:752-761. [8] 程思微, 张辉,沈林成,等.基于GDE3算法的侦察卫星星座优化设计[J].系统仿真学报,2009,21(2):586-589. CHENG Si-wei, ZHANG Hui, SHEN Lin-cheng,et al. Optimization of Regional Coverage Reconnaissance Satellite Constellation by GDE3 Algorithm[J].Journal of System Simulation, 2009, 21(2):586-589. [9] KUKKONEN S, LAMPINEN J. GDE3: The Third Evolution Step in Generalized Differential Evolution [C]∥Proceedings of the 2005 Congress on Evolutionary Computation (CEC 2005).Edinburgh, Scotland, 2005:443-450. [10] SWAGATAM Das, AMIT Konar.Two Improved Differential Evolution Schemes for Faster Global Search[C]∥ Proceeding of the 2005 Conference on Genetic and Evolutionary Computation.New York,2005: 991-998. [11] BREST J, BOSKOVIC B, GREINER S. Performance Comparison of Self-Adaptive and Adaptive Differential Evolution Algorithms Soft Computing-A Fusion of Foundations[J]. Methodologies and Applications, 2007,11(7):617-629. [12] 王博,安玮,周一宇.跟踪传感器空域覆盖性能分析[J].航天控制,2010,27(6):90-94. WANG Bo,AN Wei,ZHOU Yi-yu.Analysis on Airspace Coverage Performance of Tracking Sensors[J].Aerospace Control, 2000,27(6):90-94. [13] 王博,周一宇,鲁建华,等.基于实值粒子群优化的STSS系统传感器管理算法研究[J].系统仿真学报,2009, 21(22): 7287-7291. WANG Bo, ZHOU Yi-yu, LU Jian-Hua,et al.Research on Sensor Management Algorithm of STSS Based on Real-number Particle Swarm Optimization[J].Journal of System Simulation ,2009, 21(22): 7287-7291. [14] 牛轶峰,梁光霞,沈林成.空间预警系统建立导弹目标优先级的多属性决策[J].现代防御技术, 2006, 34(4): 1-5. NIU Yi-feng, LIANG Guang-xia, SHEN Lin-cheng.Establishment of Missile Target Priority by Space Early Warning System[J].Modern Defence Technolgy, 2006, 34(4): 1-5.1.2 控制参数自适应调整策略
2 低轨预警系统优化设计目标建模
2.1 空间覆盖建模



2.2 定位精度建模
2.3 星座成本模型
3 基于selfGDE3的系统优化设计
3.1 多目标函数及编码

3.2 仿真参数
3.3 实验结果及系统性能分析

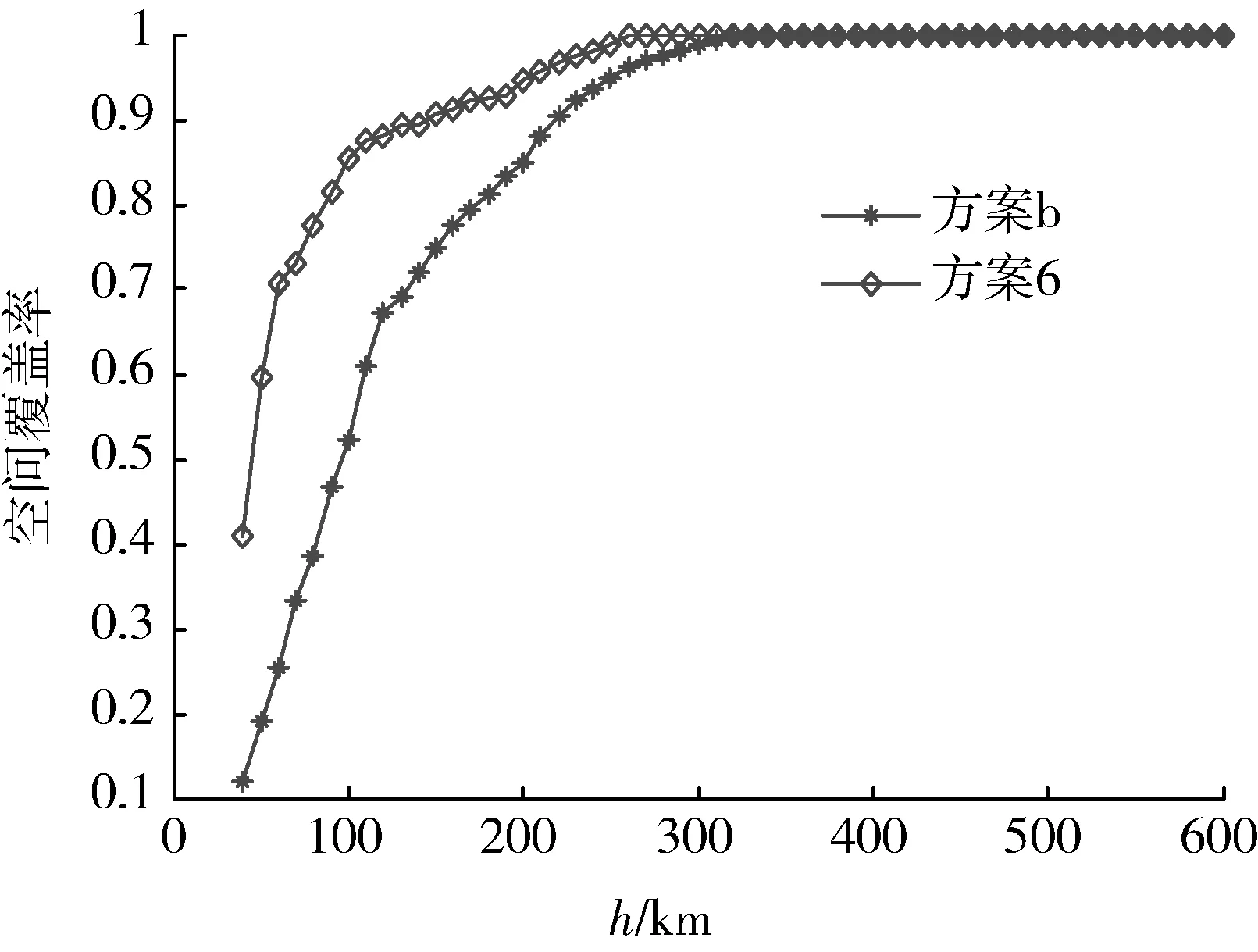

4 结束语
