基于GIS的边坡三维极限平衡模型研究

叶长锋 YE Chang-feng；刘翔宇 LIU Xiang-yu

（国核电力规划设计研究院，北京100095）

0 引言

在过去的几十年中，国内外学者对边坡三维稳定性分析问题进行了广泛而深入的研究，先后提出了一些三维边坡稳定分析方法，其中大多数都是对二维极限平衡法的扩展。回顾前人的成果可以看到，自20世纪60年代以来，不少学者进行了滑坡稳定性三维分析理论研究工作。其中，Hungr等、chen和Chameau、Lam和Fredlund分别将简化的Bishop法、Spencer法、Morgenstern和Spencer法由二维扩展到三维，其缺点是为了使问题静定，必须引入大量假设，并且该类方法涉及复杂的三维运算和非线性方程组的求解，迭代计算不可避免。总的来说，三维稳定性评价方法有了突破性的进展，但离实际应用尚有一定距离。

1 基于GIS的栅格数据结构

对于边坡三维稳定分析问题主要涉及复杂空间分布的地形、地层及岩土体物理力学参数等信息，将该类信息与GIS的栅格数据层或矢量数据相结合，有利于使传统的基于柱体单元的边坡稳定性分析模型向三维模型转化。GIS的栅格数据是用连续的大小相同的像素单元来表现每个格子相对应的值，一个栅格代表一个属性值，这可以是地面高程、各地层、不连续面、地下水或者滑动面等属性。矢量数据表现为三种典型的几何形式：点、线、面，其相应的属性数据保存在数据库中。由于滑坡体滑动面上的滑动力、正应力以及孔隙水压力不能显式获得。因此，基于Mohr-Coulomb强度准则采用差分形式进行计算：

所有与边坡相关的空间数据均可以表示为基于栅格单元的GIS栅格数据形式，由此可采用一个基于柱体单元的三维模型，即可推导出边坡的稳定安全系数。

2 基于GIS的边坡三维极限平衡分析模型

采用统一的数据结构和算法，基于GIS的栅格数据结构的极限平衡分析模型如下所示。

2.1 修正的Hovland三维扩展模型

谢谟文[2]对Hovland模型做进一步改进，主要体现在平衡了滑动面上的水平力。

图1 修正的Hovland模型

同样，提取图1所示滑动范围内某一柱体单元，进行受力状态分析，由此求得安全系数计算式为（2）：

2.2 Bishop三维扩展模型

二维Bishop[3]模型在工程实践中广泛应用，三维Bishop[2]扩展模型主要是基于以下两点假定：①忽略柱体单元的垂直面上的垂直向剪切力；②各柱体单元的垂直方向力的平衡式和整个滑体的力矩平衡满足求解未知力。

图2 三维Bishop模型

简易Bishop模型考虑了柱体单元垂直方向力的平衡和力矩的平衡，将二者联立起来求得安全系数，但未考虑水平方向力的平衡，其求解式表达如下：

2.3 Janbu三维扩展模型 三维Janbu[2]扩展模型以柱体垂直向和水平向力平衡的耦合来计算安全系数，未考虑力矩的平衡，ASP为柱体滑动面的倾斜方向，AvrASP在X-Y平面上表示的滑动方向。由于安全系数隐含需要进行迭代计算，表达式如下：

3 案例分析

该算例为一各向同性均质人工边坡，其滑动面为对称的球状弧形滑动面。图3为球状滑面与坡体物质特性。Baligh与Azzouz采用闭合形式解对该坡体进行了研究，计算的三维安全系数为1.402。Hungr等[6]使用CLARA模型对该问题进行求解，得到的安全系数为1.422。Lam和Fredlund[7]利用三维边坡模型对该问题求解，安全系数介于1.386和1.402之间，离散范围为1200到540。Huang等安全系数的计算范围大于Lam与Fredlund，是由于离散范围的不同。结果表明，随着离散范围的增加安全系数也同样增大，当具有足够的计算范围（列数为9238，栅格单元大小为），安全系数的计算值采用闭合解的误差大约在0.7%。

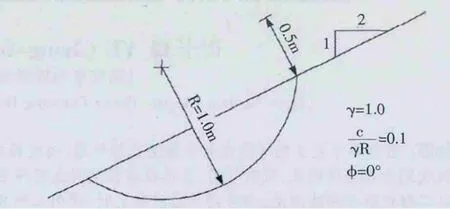
图3 模型示意图

应用基于GIS的三维极限平衡模型计算得到的安全系数与栅格单元数量关系如图4所示。

图4 安全系数的计算值与栅格数量

4 结论

本文介绍了如何将与边坡有关的数据表示为基于栅格单元的GIS栅格数据结构，采用基于栅格数据结构的柱体单元三维模型来推导计算边坡的稳定安全系数。利用基于GIS的栅格数据结构来推导四个边坡极限平衡模型的三维扩展，建立了基于GIS栅格数据格式的边坡稳定性三维极限平衡分析模型，并采用案例进行了推导。

[1]Hovland H J.Three-dimensional slope stability analysis method.Journal of the Geotechnical Engineering，Division Proceedings of the American Society of Civil Engineers 1977，103（GT9）：971-986.

[2]谢谟文，蔡美峰.信息边坡工程学的理论与实践[M].科学出版社，2005.

[3]Bishop A W.The use of the slip circle in the stability analysis of slope，Geotechnique，1955，5（1）.

[4]陈祖煜，弥宏亮，汪小刚.边坡稳定三维分析的极限平衡方法[J].岩土土程学报，2001，23（5）：525-529.

[5]Baligh，M.M.，Azzouz，A.S.End Effects on the Stability of Cohesive Slopes.Journal of the Geotechnical Engineering Division，ASCE，1975，101（11）：1105-1117.

[6]Hungr，O.，Salgado，F.M.，Byrne，P.M.Evaluation of a Threedimensional Method of Slope Stability Analysis.Canadian Geotechnical Journal，1989，26：679-686.

[7]Lam，L.，Fredlund，D.G.A General Limit Equilibrium Model for Three-dimensional Slope Stability Analysis.Canadian Geotechnical Journal，1993，30：905-919.