图的谱矩公式研究
2014-07-08吴亚平付捷
吴亚平,付捷
(江汉大学数学与计算机科学学院,湖北武汉430056)
图的谱矩公式研究
吴亚平,付捷
(江汉大学数学与计算机科学学院,湖北武汉430056)
重构猜想的研究中涉及的一个问题是找出图不变量的完全组。由于图的第k阶谱矩等于图中长为k的闭途径的条数,可知谱矩序列是图的一个重要不变量。通过研究图的结构特征,首先确定能生成长为8的闭途径的所有子图,然后给出图的第8阶谱矩计算公式。
邻接矩阵;第k阶谱矩;星树;单圈图;双圈图
0 引言
1942年Kelly和Ulam[1]提出重构猜想,重构猜想是图论中至今尚未解决的三大难题之一。找出图不变量的完全组,即找出可以完全确定一个图的一组参数,是重构猜想研究中涉及的一个重要问题。目前,图不变量的完全组仍未确定。已研究的重要参数有:点连通度、边连通度、独立数、色数、最长路长、围长、周长、最大匹配数、度序列等等。图的第k阶谱矩等于图中长为k的闭途径的条数,可知谱矩序列是图的一个重要不变量。因此图的第k阶谱矩计算公式的确定对研究重构猜想是有意义的。
猜想[1](重构猜想)如果G是至少有三个顶点的简单图,则G由它的顶点删除子图(的同构类)序列唯一确定。
1987年Cvetkovíc和Rowlinson[2]证明了图的第1~4阶谱矩的计算公式,并分别给出树和单圈图谱矩序最小和最大的图。2009年范琼和吴亚平[3]给出图的第5阶和第6阶谱矩的计算公式。2012年吴亚平等[4]给出树的第8阶谱矩计算公式。2013年吴亚平等[5]给出图的第7阶谱矩计算公式。近些年,谱矩吸引了越来越多人研究[6-14]。作为文献[4]和[5]的延续,本文给出任一简单图的第8阶谱矩计算公式。
1 预备知识
本文中我们只考虑简单图。本文中出现而未介绍的定义参照文献[1]。设G=(VG,EG),其中VG表示G的顶点集,EG表示G的边集,称G是一|VG|阶图。若G中由顶点和边构成的一个交替序列v0e1v1e2v2…vm-1emvm满足边ei的两个端点为vi-1和vi,i=1,…,m,则称此序列为G的一条(v0,vk)-途径。若v0=vk,则称它是一条闭途径。G是一n阶连通图满足|EG|=n-1+k,这里k=0,1,…,,若k=0,则称G是一棵树;若k=1,则称G是单圈图;若k=2,则称G是双圈图。有一个顶点邻接于其他所有顶点的树称为星树,n个顶点星树记为K1,n-1。星树中最大度点称为它的中心。图中度为1的点称为悬挂点。
n阶图G的邻接矩阵A(G)=[aij]n×n,这里,(i,j=1,…,n)。由于邻接矩阵A(G)是n阶实对称矩阵,则其n个特征值λ1,λ2,…,λn均为实数。图G的第k阶谱矩k=0,1,…,n-1。图G的谱矩序列记为(S0(G),S1(G),…,Sn-1(G))。
引理1[2]图G的第k阶谱矩等于G中长为k的闭途径的条数。
引理2[2]设G是n阶图,则S0(G)=n,
S1(G)=l,
S2(G)=2 m,
S3(G)=6 t,
S4(G)=2 m+4 p+8 q,
其中l、m、t分别表示图中环、边、三角形的个数,p、q分别表示相邻边对和四边形的个数。
引理3[3]设G是n阶图,则

其中ci表示G中圈子图Ci的个数,i=3,4,5,6;pi表示G中路子图Pi的个数,i=2,3,4;k1,3表示G中星树K1,3的个数;分别表示G中带一个悬挂点的3圈子图和带一个悬挂点的4圈子图的个数;a3,3表示G中2圈长为3且有一个公共点的5阶双圈图A5(3,3)的个数;b3,3表示G中2圈长为3且有一条公共边的4阶双圈图B4(3,3)的个数。
引理4[4]设T是n阶树,则
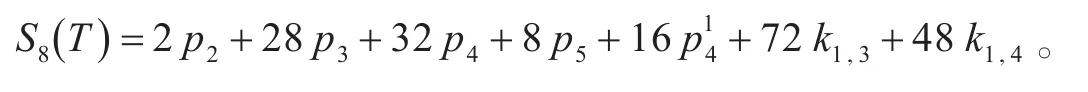
引理5[5]设G是n阶图,则
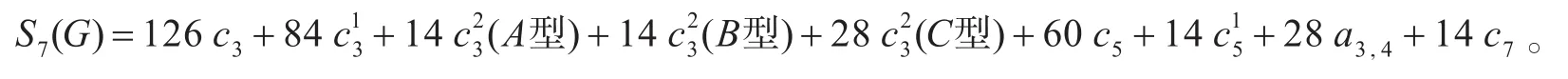
引理6[3]设T是一棵n阶树,则T中长为i=2k的闭途径只可能存在于T中阶数不超过k的所有子图中。
2 主要结果
定理1令是圈Ck中某点与路P2某个端点粘合所得图,令
(A型)是圈Ck中某点与星树K1,2中心点粘合所得图,(D型)是圈Ck中某点与路P3某个端点粘合所得图,则2×4+8=16;类似于的系数都是16。下面计算其余的系数。

计算c3的系数。将C3三个顶点分别标记为a,b,c。从a点出发,第一条边为ab长为8的闭途径:ababacbca、ababcacba、ababcbaca、ababcabca、abacabcba、abacacbca、abacbabca、abacbacba、abacacaba、abacbcaca、abacbcbca、abcababca、abcabacba、abcabcaca、abcabcaba、abcabcbca、abcacabca、abcacacba、ab⁃cacbaba、abcacbaca、abcacbcba、abcbabaca、abcbacaba、abcbacaca、abcbacbca、abcbcabca、abcbcacba、abcbcba⁃ca,共有28条。从a点出发,第一条边为ac长为8的闭途径同样有28条,即从a点出发长为8的闭途径共有56条,所以C3能生成56×3=168条长为8的闭途径。
计算a3,3的系数。将A5(3,3)中顶点按逆时针依次标记为a,b,c,d,e。
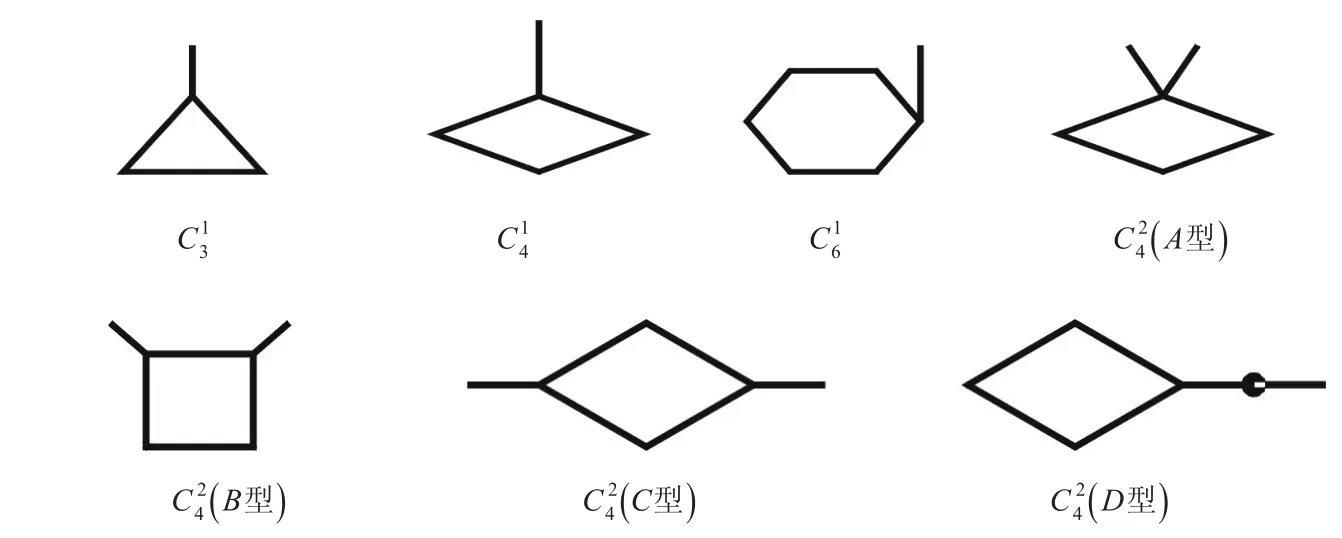
图1 围长为3、4、6边数分别为4、5或6、7的单圈图Fig.1Unicyclic graph with girth of 3,4,6 and edge numbers of 4,5 or 6,7
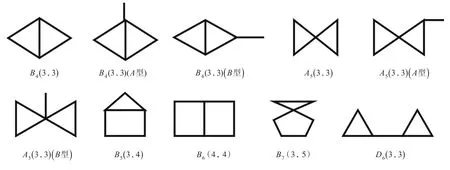
图2 生成长为8的闭途径的双圈图Fig.2Bicyclic graph of generating closed walks of length 8
从a点出发,第一条边为ac,第二条边为ca长为8的闭途径:acabcedca、acabcdeca、acacedcba、acacdecba,共4条;第一条边为ac,第二条边为cb长为8的闭途径:acbacdeca、acbacedca、acbcedcba、acbcdecba,共4条;第一条边为ac,第二条边为ce长为8的闭途径:acecedcba、acededcba、acedcabca、acedcacba、acedcbaba、acedcbaca、acedcbcba、acedcdcba、acedcecba,共9条;根据对称性,第一条边为ac,第二条边为cd长为8的闭途径也有9条。因此从a点出发第一条边为ac长为8的闭途径共有26条。从a点出发,第一条边为ab,第二条边为ba长为8的闭途径:ababcdeca、ababcedca,共2条;第一条边为ab,第二条边为bc,第三条边为ca(ce)长为8的闭途径:abcacdeca、abcacedca、abcbcdeca、abcbcedca、abcededca、abcecabca、abcedcaca、abcedcbca、abcedceca、abcedcdca、abcecdeca、abcecedca,共12条。根据对称性,第一条边为ab,第二条边为bc,第三条边为cd长为8的闭途径也有8条。因此从a点出发第一条边为ab长为8的闭途径共有22条,即从点a出发长为8的闭途径共有48条。根据对称性,分别从点b,d,e出发长为8的闭途径都是48条。
从c点出发,第一条边为ca,第二条边为ab长为8的闭途径:cababcedc、cababcdec、cabcacdec、cab⁃cacedc、cabcbcdec、cabcbcedc、cabcdedec、cabcdecac、cabcdecbc、cabcdecdc、cabcdecec、cabcdcdec、cabcdcedc,共13条;第一条边为ca,第二条边为ac长为8的闭途径:cacabcdec、cacabcedc、cacbacedc、cacbacedc、caced⁃cabc、cacedcbac,共6条,因此从c点出发,第一条边为ca长为8的闭途径共19条。根据对称性,从c点出发长为8的闭途径是19×4=76条。所以A5(3,3)共生成48×4+76=268条长为8的闭途径。
计算a3,3(A型)的系数。将A5(3,3)(A型)中悬挂点标记为a,子图A5(3,3)中点按逆时针依次标记为b,c,d,e,f,其中悬挂点的邻点标记为b。经计算可知,分别从a,b,c,f出发长为8的闭途径都是4条;从e,d出发长为8的闭途径都是8条。因此A5(3,3)(A型)共生成4×4+8×2=32条长为8的闭途径。
计算a3,3(B型)的系数。从A5(3,3)(B型)最大度点出发有24条长为8的闭途径,从其余各点出发分别有8条长为8的闭回路,因此A5(3,3)(B型)共生成64条长为8的闭途径。
计算b3,3的系数。将B4(3,3)中2个2度点分别标记为a,c;将2个3度点分别标记为b,d。从a点出发,第一条边为ab,第二条边为ba长为8的闭途径:ababcdbda、ababdbcda、ababdcbda、abadbcdba、abadbdcba,共5条;第一条边为ab,第二条边为bd长为8的闭途径:abdabcdba、abdabdcba、abdadbcda、abdadcbda、abdbabcda、abdbadcba、abdbdcbda、abdbcbcda、abdbcdada、abdbcdbda、abdbcdcda、abdcbabda、ab⁃dcbabdba、abdcbdada、abdcbdbda、abdcbdcda、abdcbcbda、abdcdcbda、abdcdbcda,共19条;第一条边为ab,第二条边为bc长为8的闭途径:abcbdbcda、abcdabdba、abcdadbda、abcdbabda、abcdbadba、abcdbcbda、abcdbdaba、abcdbdada、abcdbdbda、abcdbdcda,共10条。因此从a点出发共有(5+19+10)×2=68条长为8的闭途径。
从b点出发,第一条边为ba长为8的闭途径:babadcbda、babadbcda、babdabcda、babdadcba、babdcba⁃da、babdcbcda、babcbdcda、babcdabda、babcdadba、babcdbaba、babcdbada、babcdbcda、babcdcbda、badabcdba、badabdcba、badadcbda、badadbcda、badcbabda、badcbadba、badcbcbda、badcbcdba、badcbdaba、badcbdada、badcbdbda、badcbdcba、badcbdcda、badcdcbda、badcdbcba、badcdbcda、badbabcda、badbadcba、badccbcda、bad⁃bcdaba、badbcdada、badbcdcba、badbcdcda、badbcdbda、badbdcbda、badcdbcda,共39条。根据对称性,从b点出发,第一条边为bc长为8的闭途径也有39条。从b点出发,第一条边为bd,第二条边为da长为8的闭途径:bdababdeb、bdababcdb、bdabdadcb、bdabdbcdb、bdabdcbcb、bdabdcdcb、bdabcbcdb、bdabcbdcb、bdabcdadb、bdabcdbab、bdabcdbcb、bdabcdbdb、bdabcdcdb、bdadabcdb、bdadabdcb、bdadbadcb、bdadbcdab、bdadcbadb、bdadcbdab,共19条;根据对称性,第一条边为bd,第二条边为dc长为8的闭途径也有19条;第一条边为bd,第二条边为db,第三条边为ba长为8的闭途径:bdbabadcb、bdbadadcb、bdbadbcdb、bdbadbdcb、bdbadcbab、bdbadcbcb、bdbadcbdb、bdbadcdcb,共8条;根据对称性,第一条边为bd,第二条边为db,第三条边为bc长为8的闭途径也有8条;第一条边为bd,第二条边为db,第三条边为bd,长为8的闭途径:bdbdabcdb、bdbdabdcb、bdbdcbadb、bdbdcbdab,bdbdbadcb、bdbdbcdab,共6条;即从b点出发,第一条边为bd长为8的闭途径有19×2+8×2+6=60条。因此从b点出发共有39×2+60=138条长为8的闭途径,可知B4(3,3)共生成(68+138)×2=412条长为8的闭途径。
计算d3,3的系数。分别从D6(3,3)中2度点出发都有4条长为8的闭途径;分别从D6(3,3)中3度点出发都有8条长为8的闭途径,即D6(3,3)共生成4×4+8×2=32条长为8的闭途径。
计算b3,3(A型)的系数。将B4(3,3)(A型)4度点标记为a,3度点标记为b,2个2度点分别标记为c,d,悬挂点标记为e。下面考虑子图B4(3,3)生成长为6的闭途径。从a点出发,第一条边为ab长为6的闭途径:abcabda、abcadba、abdabca、abdacba、abacbda、abadbca,共6条;第一条边为ac长为6的闭途径:acbadba、acbdaba、acbabda,共3条;根据对称性,第一条边为ad长为6的闭途径也有3条。由于在长为6的闭途径中加上aea就能构成长为8的闭途径,因此,在B4(3,3)(A型)中,从a点出发长为8的闭途径6×2+3×2×2+12=36条。类似分析可知从b点出发有24条长为8的闭途径,从c,d,e点出发分别有12条长为8的闭途径。B4(3,3)(A型)共生成96条长为8的闭途径。
计算b3,3(B型)的系数。将B4(3,3)(B型)中悬挂点标记为e,悬挂点的邻点标记为d,2个3度点分别标记为a,b,2度点标记为c。同B4(3,3)(A型)分析,可知分别从a,b点出发都有12条长为8的闭途径;分别从c,e点出发都有6条长为8的闭途径;从d点出发有12条长为8的闭途径,即B4(3,3)(B型)共生成48条长为8的闭途径。
计算c4的系数。将C4中点按逆时针方向依次标记为a,b,c,d。从a点出发,第一条边为ab长为8的闭途径:ababadcba、abababcda、ababcbcda、babacdaba、babacdada、ababcdcda、abadabcda、abadadcba、babdcbaba、abadcbada、abadcbcba、abadcbcda、abadcdcba、abcbabcda、abcbadcba、abcbadcda、abcbcbcda、ab⁃cbcdaba、abcbcdada、abcbcdcda、abcdababa、abcdabada、abcdabcba、abcdabcda、abcdadaba、abcdadada、abc⁃dadcba、abcdadcda、abcdcbada、abcdcbcda、abcdcdada、abcdcdaba、abcdcdcda,共33条;根据对称性,第一条边为ad长为8的闭途径也有33条。从a点出发共66条长为8的闭途径,根据对称性,C4共生成66×4=264条长为8的闭途径。
计算b3,4的系数。从B6(3,4)中每个顶点出发都有8条长为8的闭途径,即B6(3,4)共生成40条长为8的闭途径。
计算b4,4的系数。从B6(4,4)中3度点出发,有8条长为8的闭途径;从B6(4,4)中2度点出发,有4条长为8的闭途径,即B6(4,4)共生成8×2+4×4=32条长为8的闭途径。
计算b3,5的系数。从B7(3,5)中4度点出发,有8条长为8的闭途径;从B7(3,5)中2度点出发,有4条长为8的闭途径,即B7(3,5)共生成8+4×6=32条长为8的闭途径。
故定理2成立。
(References)
[1]WEST D B.图论导引:英文版[M].2版.北京:机械工业出版社,2004.
[2]CVETKOVIC D,ROWLINSON P.Spectra of unicyclic graphs[J].Graph and Combinatorics,1987,3(1):7-23.
[3]范琼,吴亚平.图的谱矩序列与图的排序[J].武汉大学学报:理学版,2009,55(6):1-4.
[4]吴亚平,吕康南,付捷.树的谱矩研究[J].江汉大学学报:自然科学版,2012,40(6):1-4.
[5]吴亚平,付捷,吕康南.图的奇数阶谱矩研究[J].江汉大学学报:自然科学版,2013,41(3):19-22.
[6]ANDRIANTIANA E,WAGNER S.Spectral moments of trees with given degree sequence[J].Linear Algebra and its Appli⁃cations,2013,439(10):3980-4002.
[7]CHENG B,LIUB L.Lexicographical ordering by spectral moments of trees with k pendant vertices and integer partitions[J].Applied Mathematics Letters,2012,25(5):858-861.
[8]CHENG B,LIU B L,LIU J X.On the spectral moments of unicyclic graphs with fixed diameter[J].Linear Algebra and its Applications,2012,437(3):1123-1131.
[9]GUTMAN I,ROSENFELD V R.Spectral moments of polymer graphs[J].Theoretica Chimica Acta,1996,93(1):191-197.
[10]LI S C,ZHANG H H,ZHANG M J.On the spectral moment of graphs with k cut edges[J].Electronic Journal of Linear Algebra,2013,26(2):718-731.
[11]PAN X F,HU X L,LIU X G,et al.The spectral moments of trees with given maximum degree[J].Applied Mathematics Letters,2011,24(7):1265-1268.
[12]PAN X F,LIU X G,LIU H Q.On the spectral moment of quasi-trees[J].Linear Algebra and its Applications,2012,436(5):927-934.
[13]WU Y P,LIU H Q.Lexicographical ordering by spectral moments of trees with a prescribed diameter[J].Linear Algebra and its Applications,2010,433(11):1707-1713.
[14]WU Y P,FAN Q.On the lexicographical ordering by spectral moments of bicyclic graphs[J].Ars Combinatorics,2014,114(2):213-222.
(责任编辑:强士端)
Spectral Moment Formula of Graphs
WU Yaping,FU Jie
(School of Mathematics and Computer Science,Jianghan University,Wuhan 430056,Hubei,China)
One problem of the reconstruction conjecture is:find a complete set of invariants of a graph.The spectral moment sequence is an important invariant of a graph,since the kthspectral mo⁃ment of a graph is equal to the number of closed walks of length k.On the structure feature of a graph,first finds all connected subgraphs which can generate closed walks of length eight,then pro⁃vides 8thspectral moment calculation formula.
adjacent matrix;kthspectral moment;star;unicyclic graph;bicyclic graph
O157.5
A
1673-0143(2014)06-0045-07
2014-11-02
武汉市科技局资助项目(201250499145-24,2013011001010484);湖北省教育厅一般项目(B20114503)
吴亚平(1979—),女,讲师,博士,研究方向:图论。
