基于可解空间法的视景路径规划仿真系统设计
2014-07-08周静付绪昌
周静,付绪昌
(1.江汉大学数学与计算机科学学院,湖北武汉430056;2.鸿富锦精密工业有限公司制造执行系统开发课,湖北武汉430204)
基于可解空间法的视景路径规划仿真系统设计
周静1,付绪昌2
(1.江汉大学数学与计算机科学学院,湖北武汉430056;2.鸿富锦精密工业有限公司制造执行系统开发课,湖北武汉430204)
提出一种新的可解空间粒子群寻路算法,并实现Vega Prime(VP)三维视景路径规划仿真系统。算法假设初始化的每个粒子都是一个潜在的可行解,都可到达终点。每个粒子在迭代的过程中不断更新位置,并记录下它们所经过的路径点的个数;迭代结束后,找出到达终点的粒子中路径点个数最少的粒子,将该粒子每次迭代时所经过的最优位置作为寻路路线。同时在VP大地图场景中,为矩形障碍物添加一个圆形的坡度,较好地解决了算法易陷入局部最优解的缺陷。该仿真系统的正确运行验证了算法的有效性及系统的实用性。
可解空间法;视景仿真;路径规划;圆形坡度
0 引言
随着视景仿真技术的应用越来越广泛,基于Vega Prime(VP)的视景仿真技术也得到了不断的发展,在民用、商用、军事等各个领域中都得到了广泛的应用[1-2]。利用VP构建三维场景及模型,并建立相应的不同对象之间的关系以及地面检测、碰撞检测[3]。在MFC中搭建好VP环境,调用VP文件,并实现相关消息响应,计算出场景地形中的障碍坐标列表。然后将改进的粒子群算法移植到MFC程序,粒子群算法获取障碍坐标,构建相应的地图矩阵,计算出寻路路径后将路径坐标列表返回到MFC程序,MFC程序根据获取的路径坐标实现自动寻路。
1 VP视景仿真平台的设计与实现
基于MFC的VP应用程序主要用到VP库中的API。基于STL(标准模板库)和C++的API显得非常紧凑和灵活。VP的API通过模板和继承性的使用使得仿真循环更加简洁而有效。实时控制包括定义ACF、配置ACF和系统、运行仿真循环以及最后退出仿真循环。
1.1 VP应用程序的主循环
主循环{
获取对象(如前视观察者等)的位姿矢量(上一帧);
获取用户键盘输入控制;
根据对象上一帧的位姿和输入控制来计算位姿;
碰撞检测并对计算所得位姿进行调整;
赋予对象调整后的位姿;
更新帧;}
1.2 VP地图编码
地图编码主要实现步骤如下:1)定义点坐标结构体。
2)地图编码初始化,即无障碍图。
3)障碍坐标初始化,在定义的地图矩阵中赋值。
1.3 通道添加
实现俯视通道并绑定观察者位置的实现步骤如下:
1)实现俯视效果。
2)定义俯视通道并设置其在窗口中的位置,关联窗口,关联图形状态。
3)定义俯视观察者,并将观察者和通道并联。
4)在主循环中根据控制更改俯视观察者的位姿,即可实现通过俯视通道观察的效果。
图1为添加通道的示意图,根据需求控制通道宽度就能符合使用者的要求。
图1 通道添加示意图Fig.1Schematic diagram of adding channel
1.4 固定地图俯视图
如果将俯视图通道的观察者设置为看向小车,这样会出现当小车在转向时,小车的方向没有发生偏转,而是地图在旋转,不利于观察小车行进路线。利用LynX Prime(LP)修改通道观察者参数设置,将观察者的俯视通道固定在地图中心点,这样地形就不会旋转了,只有小车在行进的过程中因改变方向而偏转。
图2是由像素点1 080×720转化为的1 000×1 000大小的三维视景地图,障碍物和坐标系均进行了计算转化:X坐标乘以1 000/1 080;Y坐标乘以1 000/720。图2中左边是整个设计地图的全景俯视通道;右上为当前智能体行走主视图通道,右下是粒子将要到达的目标点的俯视图通道。

图2 初始化的系统界面图Fig.2Interface of the initialization system
2 可解空间粒子群寻路算法设计
2.1 算法设计思想
在改进标准粒子群算法[4-5]的基础上,提出可解空间粒子群寻路算法(以下简称可解空间法),其流程图如图3所示。
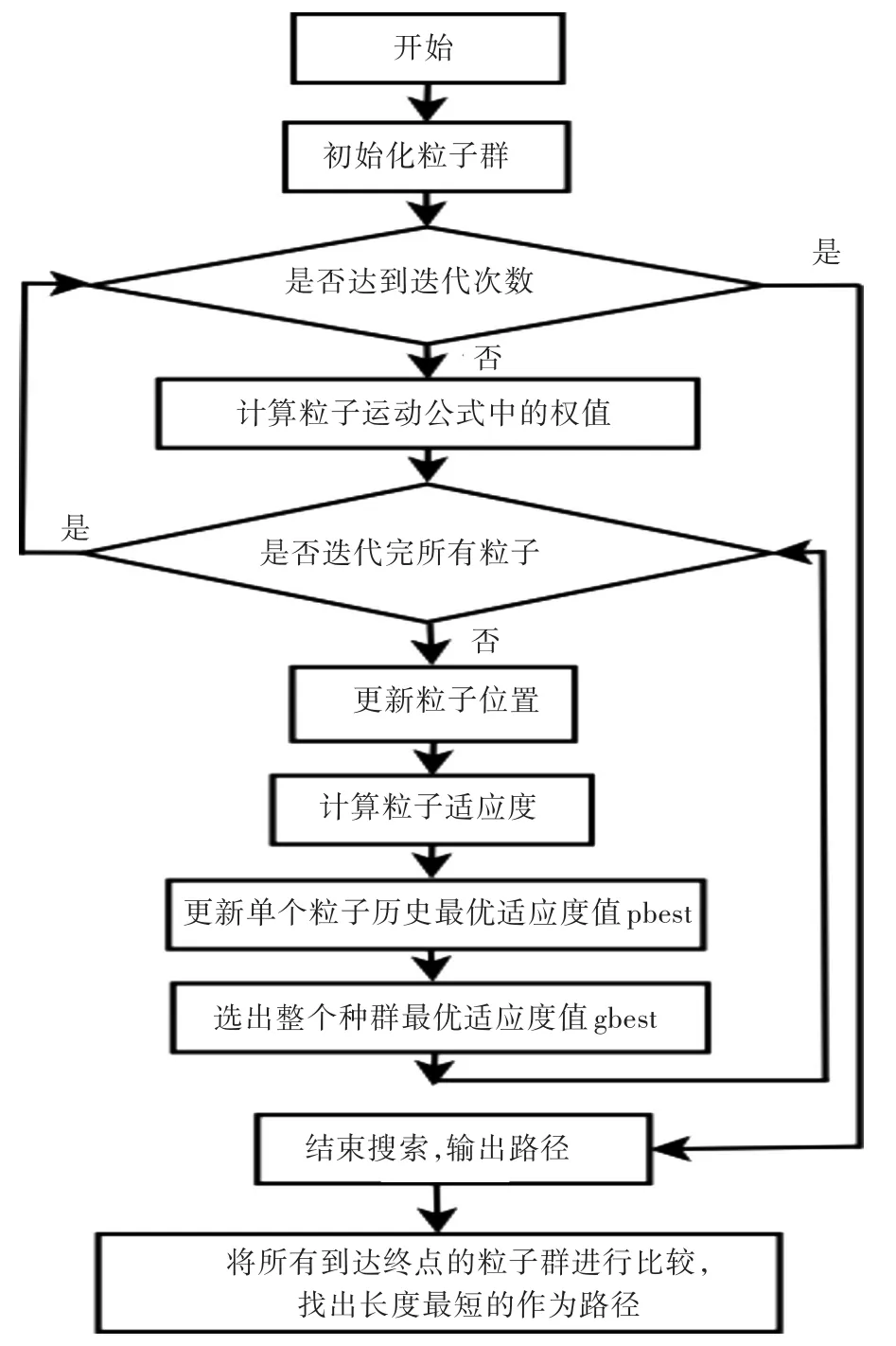
图3 可解空间法流程图Fig.3Solvable-space algorithm flow chart
可解空间法的设计思想为:假设初始化的每个粒子都是一个潜在的可行解空间,每个粒子在不断更新位置(只要比其历史最优适应度值pbest小,则更新至当前路径点,这里的粒子适应度表示当前粒子所处位置距离目标的马氏距离),经过完全迭代后,每个粒子都保存了生命周期中所经过的路径点坐标,在满足搜索结束条件后,需要对每个粒子的路径进行一个评估,就是找出群体中到达终点的所有粒子中所走路径最短的一个个体的路径(即该个体所经历的路径点个数最少),此路径便是此次寻路最优的解。实现本算法也就是比较每个粒子的路径长度(即路径点计数count值)的大小,可以借用选择排序中第一次循环找到所有数据中最大(或最小)的值放在第一个位置,将拥有count值最小的粒子路径点逐个输出并显示在地图上即可。将这种思想的粒子群寻路算法称为“可解空间法”。
2.2 寻找最短路径代码实现
找出群体中到达终点的所有粒子中所走路径最短的一个个体的路径代码如下:
for(i=1;i<PSO_popsize;i++){//搜索最优,相当于选择排序第一步的过程
cout<<PSO_pop[i].pbest<<endl;//每个粒子的最优适应度值
if(PSO_pop[i].pbest<=sqrt(2.0))//粒子最终最佳位置=终点
if(PSO_pop[i].count<PSO_pop[i-1].count)
bestpath=i;}
if(bestpath>-1){//判断路径存在与否,若存在,将路径保存
pathfound=true;
for(i=0;i<PSO_pop[bestpath].count;i++){
setPos(PSO_pop[bestpath].Epbest_posX[i],PSO_pop[bestpath].Epbest_posY[i]);cout<<"("<<PSO_pop [bestpath].Epbest_posX[i]<<","<<PSO_pop[bestpath].Epbest_posY[i]<<")"<<endl;}}
else{cout<<"寻路失败!"<<endl;
return;}
代码中的Epbest_posX变量是指路径最短的粒子的x坐标,Epbest_posY变量是指路径最短的粒子的y坐标。整个粒子群的迭代次数为PSO_maxgen,大小为PSO_popsize,算法时间复杂度为O(PSO_max⁃gen*PSO_popsize*PSO_popsize)。
2.3 算法运行结果
在平面空间模型的寻路算法研究中,应用可解空间法运行结果如图4所示。从图4可看出,可解空间法可以完成路径规划任务。从可解空间法的思路可看出,它属于先局部路径规划出可解路径,然后再在这些可解路径上求出长度最短的路径并输出的局部启发性规划算法。

图4 可解空间法在平面空间中的寻路效果Fig.4Effect with solvable-space algorithm to find path in planar pace
3 VP平台下寻路算法的优化
3.1 寻路算法引入VP-MFC程序
VP程序提供给可解空间粒子群寻路算法的参数为:地图大小(长、宽)、起点和终点坐标(x,y,z=0)、point结构体,所有障碍点坐标采用List<point>进行存储。寻路算法返回给VP程序的参数:寻路成功后,所有路径点按顺序存入list<point>列表ListPoint llPath。将该列表返回给VP程序,VP程序再根据返回的路径列表中每一个点的坐标值进行寻路。
将所设计的可解空间法应用于较大的VP地图环境寻路时,发现其仍会陷入局部最优解,这时采用给障碍物一个坡度的思想可使陷入局部最优解的粒子绕开障碍物。
3.2 局部最优解的改进
以下对该种算法原理进行建模分析,建模图如图5所示。图5中,起点A和目标点B之间有一个较大的矩形障碍,并且起点A和目标点B在障碍物对称线两边。按照粒子群路径规划方法,粒子群在寻路时,会不断逼近图中C点,在没有设置避障时,由于两点直线距离符合路径长度最短的条件,粒子会穿过图中黑色障碍物直线到达目标点B,这显然是不符合设计标准的,但是在由前文介绍的粒子群寻路算法可知,算法在迭代过程中,在C点邻域范围内没有比当前位置(C点)更优的位置,所以粒子群在搜索路径的时候,会更新停止在C点,直到迭代结束PSO算法程序运行完毕,导致粒子群寻路失败(走了一段,并且停滞在某一坐标点,C点就是一个代表),问题仿真如图6所示。从图6可以看出,坐标(8,7)充当了上述C点的角色,导致了粒子正在寻路中得到局部最优。
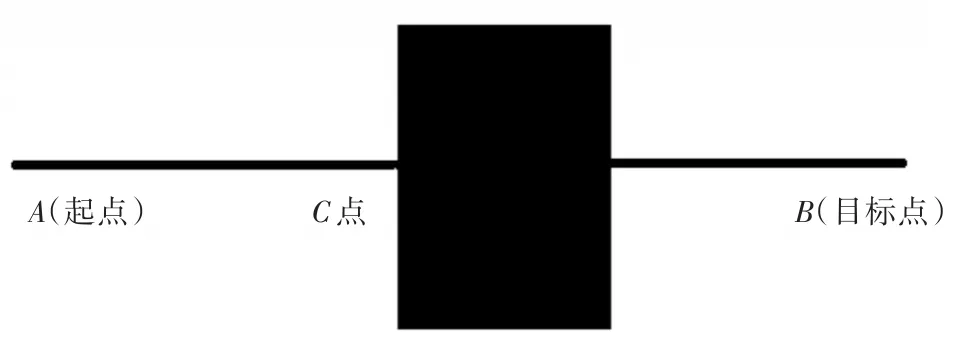
图5 基本粒子群算法陷入局部最优建模图Fig.5Modeling diagram of basic particle swarm algorithm result in falling into local optimal
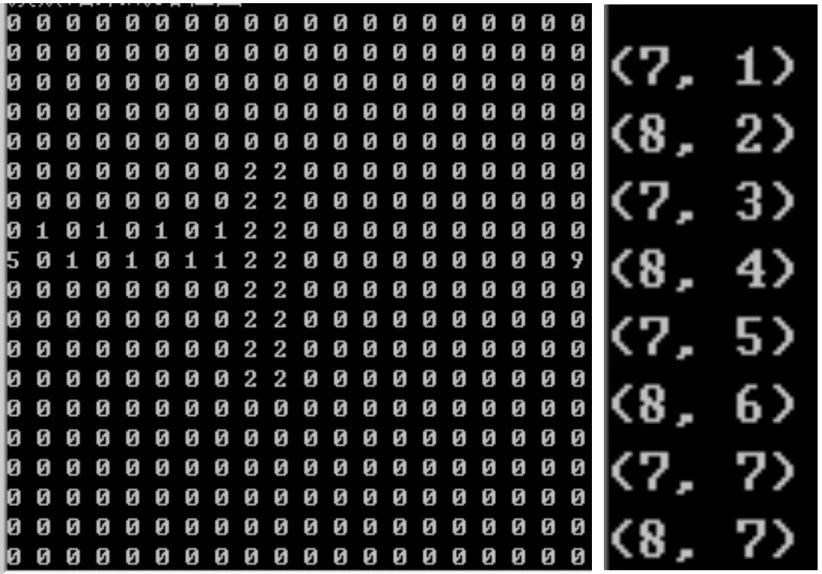
图6 陷入局部最优实验运行结果图Fig.6Experiment result of falling into local optimal
粒子群寻路算法出现上述问题的主要原因是粒子无法在障碍物的“凹角”里回退出来,没有一个坡度(弧度)让粒子群向地势低的方向行进就导致了陷入局部最优。如果将障碍物视为一个圆形(见图7),则无论粒子群在障碍物的哪一个方向(360°视角范围内)都产生了一个坡度,这样粒子群在寻路的时候就不会向着障碍物趋近,因为在距离障碍物还有段微小距离时,已经“感知”到了障碍物的威胁[6]。按照上述理论模拟扩展障碍物得到如图8结果。

图7 解决局部最优模型Fig.7The model to solve the local optimal

图8 解决局部最优仿真结果Fig.8Simulation result of solving the local optimal
在LP地图(ACF文件)中,障碍物较大设置扩展填充坐标点[7]较为繁杂,因此填充的具体做法为:将黑色障碍物坐标进行扩展,已知VP中的障碍物矩阵对顶角两个坐标点,通过这两个坐标点可以计算出对角线的中心坐标即圆心(centerX,centerY)和对角线长度的一半值即为半径R,然后进行逐个像素点填充。
为避免逐个障碍物手动扩展的庞大工作量,将障碍物扩展成为一个圆形。具体代码如下:
void setOneBarrier(int xMin,int yMin,int xMax,int yMax){
int centerX=(xMin+xMax+1)/2;
int centerY=(yMin+yMax+1)/2;
int R=int(sqrt(double((xMin-xMax)*(xMin-xMax)+(yMin-yMax)*(yMin-yMax)))/2+0.5);
for(int i=-R;i<=R;i++){
int dx=int(sqrt(double(R*R-i*i))+0.5);
for(int j=-dx;j<=dx;j++){
lBarrier.push_back(point(j+centerX,i+centerY,0));}}}
3.3 算法优化效果分析
将障碍物扩展成圆形的避障算法示意图如图9所示。在画圆过程中也会出现锯齿状边缘(见图9),计算机填充无法达到标准的圆,在栅格中更是无法避免出现锯齿的波纹,这样在较小程度上影响本次仿真效果,因为在粒子群寻路中会出现坡度不明显而陷入之前提到的那种局部最优情形,但是在实际应用中地图往往远大于本文中所使用的1 000×1 000大小的地图。

图9 粒子在扩展的圆形障碍物中的路径Fig.9Path of particles in extended circular obstacle
图9是将障碍物用“#”表示,粒子绕过障碍物用“0”表示路径,将程序中的路径规划写到TXT文档中以显示仿真优化的效果,这样可以很明显地看出粒子避障的轨迹细节,从图9看出陷入局部极值通过画圆算法在仿真实例中得到了较好的优化效果,在仿真中的效果切合理论预期。
4 路径规划仿真系统设计
仿真地图是由像素点1 080×720转化为的1 000×1 000大小的三维视景地图,其中设定23个均匀分布在地图上的障碍物坐标。将可解空间粒子群算法[8-10]用于此仿真环境中并进一步优化,大大降低粒子群陷入局部最优解找不到路径的概率,提高了粒子成功获得路径的能力。高效完成在拥有多障碍的复杂场景下展示智能避障的路径规划系统。
该仿真系统通过点击屏幕视角的任意位置,粒子群就开始寻路,待寻路算法运行完毕就开始行走,到达目标点后自动停止下来,等待用户指定下一次任务。
初始小车只能按照程序中设置好的起点和终点进行一次性的寻路,经改进后程序可以实现用鼠标点击俯视图自定义终点的多次寻路,这样可以方便有效地测试各种不同情况的寻路。由于每次寻路速度较快,不能较好地观察比较寻路路线的优劣,因此采用OpenGL画图,将粒子群所行走的路径用连续线段标记出来。
从仿真图10和图11中可以看出,使用可解空间法在大地图中寻路能力相对较好,满足了基于粒子群算法(PSO)路径规划系统设计的要求。

图10 可解空间法寻路整体效果图Fig.10Overall effect of path finding with solvable-space algorithm

图11 俯视通道放大图Fig.11Enlarge figure of overlooking channel
5 结语
提出的可解空间粒子群算法应用于路径规划中,将地图中的障碍物扩展成一定的坡度进而优化,从而改善粒子群寻路时陷入局部最优的情况。从仿真结果上看提高了粒子群搜索空间的成功率,在实际应用中满足了路径规划系统设计的要求。
(References)
[1]张德锋,王华兵,薛原,等.基于Vega Prime的视景仿真技术研究与应用[J].计算机仿真,2006,23(7):191-195.
[2]王孝平,董秀成,郑海春,等.Vega Prime实时三维虚拟现实开发技术[M].成都:西南交通大学出版社,2012:20-90.
[3]魏博,吴国平,朱士峰.基于MFC框架的Vega虚拟场景设计和实现研究[J].河南科学,2008,26(4):454-458.
[4]刘波.粒子群优化算法及其工程应用[M].北京:电子工业出版社,2010:70-110.
[5]孙超锋.基于离散粒子群算法的机器人最优路径规划研究[D].南昌:华东交通大学,2011:21-27.
[6]张昉,张雷.基于改进粒子群算法的UCAV二维路径规划[J].航空兵器,2008(6):3-7.
[7]陆枫,何云峰.计算机图形学基础[M].北京:电子工业出版社,2008:30-50.
[8]LIU X,WEI H G,ZHOU C P,et al.The path planning for UAV based on orthogonal particle swarm optimization[C]//Pro⁃ceedings of international society for optical engineering.Wuhan:SPIE,2013,8921:89210X1-89210X9.
[9]ALEJO D,COBANO J A,HEREDIA G,et al.Particle Swarm Optimization for collision-free 4D trajectory planning in Un⁃manned Aerial Vehicles[C]//2013 International Conference on Unmanned Aircraft Systems.Atlanta:IEEE,2013:298-307.
[10]DAI Y,LIU L,LI Y,et al.An improved particle swarm optimization based on cellular automata[J].International Journal of Computing Science and Mathematics,2014,5(1):94-106.
(责任编辑:曾婷)
Scene Path Planning Simulation System Design by Solvable-Space Algorithm
ZHOU Jing1,FU Xuchang2
(1.School of Mathematics and Computer Sciences,Jianghan University,Wuhan 430056,Hubei,China;2.Department of Manufacturing Execution System Devlopment,Hongfujin Percision Industry Company Limited,Wuhan 430204,Hubei,China)
A new particle swarm solvable-space pathfinding algorithm is proposed,and the Vega Prime(VP)three-dimensional visual path planning simulation system is achieved.The algorithm as⁃sumes that each initial particle is a potentially viable solution and can reach the terminal point.Dur⁃ing the full iterations,each particle updates its position continually and saves the numbers of path points.When the search ended,find the particle whose number of the path points is fewest,and set this particle′s optimal position in each iteration as the wayfinding route.Meanwhile in VP large map scene,adding a circular gradient for the rectangular obstacles can easily solve the algorithm′s de⁃fect.The simulation system runs correctly proves the practicality of the algorithm and effectiveness of the system.
solvable-space algorithm;scene simulation;path planning;circular gradient
TP391.9
A
1673-0143(2014)06-0085-07
2014-09-09
武汉市教育局教研项目(2011059,2014016);湖北省住房和城乡建设厅科研开发项目——空间信息融合的多目标协同轨迹规划应用研究
周静(1981—),女,讲师,博士,研究方向:计算机可视化仿真、图形图像处理。
