动力总成悬置系统优化及稳健性分析

童东红郝志勇

（浙江大学）

动力总成悬置系统优化及稳健性分析

童东红郝志勇

（浙江大学）

为改善动力总成悬置系统的隔振性能，以某车辆的悬置系统为研究对象，在扭矩轴坐标系下建立6自由度振动分析数学模型，阐述能量解耦的计算方法。以悬置系统振动解耦率和固有频率分布为设计目标，以悬置刚度为设计变量，采用遗传算法对该悬置系统进行优化设计，并且用蒙特卡罗模拟方法对优化结果进行稳健性分析。结果表明，优化后悬置系统的振动解耦率和频率满足设计要求，且系统设计稳健性较好。

1 前言

动力总成悬置系统作为连接动力总成与车身（或车架）的元件，其作用主要为[1]：支撑动力装置的质量；抵抗发动机产生的扭矩；减小从发动机传递到车身（或车架）的振动激励，同时衰减路面激励，减小高频结构噪声传递；缓冲汽车在加速、减速和转弯时形成的冲击力，避免发动机与周围零部件之间的碰撞，因此其设计好坏直接影响整车NVH性能的优劣。

通过选择适当的悬置系统参数（安装位置、角度和刚度），达到合理配置动力总成刚体振动模态的固有频率和实现系统振动解耦等是悬置系统设计的基本任务[2～6]。由于悬置元件在制造、加工、装配和测量过程中存在很大的误差波动，如悬置刚度的理论值与实际值通常有±15%的偏差，从而造成悬置系统性能不稳定，甚至有潜在失效的风险，所以有必要对悬置系统进行稳健性分析和优化。基于试验设计方法（Design Of Experiment，DOE），文献[7]计算分析了悬置刚度的变化对动力总成悬置系统频率配置和能量解耦率的影响；文献[8]以悬置刚度值为因素变量，以能量解耦率为目标，采用田口鲁棒设计方法对汽车动力总成悬置系统进行了稳健设计；文献[9]将悬置刚度、安装位置和角度当作正态分布的随机变量，利用6σ优化方法对悬置系统进行了解耦鲁棒优化设计。本文以某款动力总成悬置系统为研究对象，建立悬置系统的数学模型，结合工程实际在优化时以悬置刚度为优化变量，以系统振动解耦率和固有频率为优化目标，利用Matlab软件编写相应程序对悬置系统进行解耦优化设计。

2 悬置系统数学模型

动力总成悬置系统通常采用3点或4点布置，发动机有横置和纵置两种不同的布置方式，本文所研究悬置系统为3点横置布置型式。由于动力总成悬置系统的振动固有频率一般低于30 Hz，通常将发动机和变速器总成及车架视为绝对刚体，同时把各个悬置简化为沿空间3个垂直方向的弹性阻尼元件，省略支撑元件间的扭转弹性作用。动力总成悬置系统构成一个空间6自由度振动系统，如图1所示[10]。图1中，动力总成质心为C，坐标系C-XYZ为动力总成曲轴坐标系，坐标系C-XTRAYTRAZTRA为动力总成扭矩轴坐标系，q为系统广义坐标向量，ri为第i个悬置的弹性中心到动力总成质心C的位移向量。

2.1 坐标系定义

该系统中常采用3个互相关联的坐标系，即发动机曲轴坐标系C-XYZ、主惯性轴坐标系CXPYPZP，以及扭矩轴坐标系C-XTYTZT，其原点均设在动力总成质心C处，如图2所示。

曲轴坐标系的X轴平行于曲轴轴线指向发动机前端面，Z轴平行于气缸中心线指向发动机上端面，Y轴由右手定则确定。扭矩轴XT为无约束三维刚体的旋转轴，其与刚体的惯性特性和施加在刚体的转矩方向有关。动力总成受到绕曲轴的倾覆转矩作用，且由于其质量分布不均，曲轴轴线和动力总成的主惯性轴XP不重合，因此动力总成的转动既不绕着曲轴，也不绕着主惯性轴，而是绕着空间某一特定轴线，即扭矩轴。当检验动力总成的振动情况和隔振性能时，一般都在曲轴坐标系下进行分析。然而，在进行动力总成悬置系统的解耦布置设计时，则需要在动力总成的扭矩轴坐标系下进行分析[3]。在悬置系统设计初期，将悬置弹性中心落在扭矩轴上，可以使动力总成刚体模态在侧倾自由度和垂向自由度与其它自由度之间解耦。主惯性轴坐标系和扭矩轴坐标系的方位可按如下方法求得[2]：

构造动力总成惯性矩的2阶张量[ST]：

式中，JX、JY、JZ、JXY、JYZ和JZX为动力总成在曲轴坐标系下的惯性矩，可以通过试验测得或者由三维模型获取。该张量的3个特征值即为相应的主惯性矩，标准特征向量即为相应的主惯性轴在曲轴坐标系下的方向余弦。

扭矩轴XT在曲轴坐标系下的方位为：

式中，JXp、JYp和JZp为动力总成的3个主转动惯量；α、β和γ为主惯性轴在曲轴坐标系下的方位角。

扭矩轴坐标系中只有XT轴是惟一确定的，其它两条坐标轴可以有不同的选择方式，通常取ZT轴在曲轴坐标系的XCZ平面内，进而由空间基向量的性质可以确定YT轴的位置。

2.2 振动微分方程

在微小振幅作用下忽略阻尼影响，系统在扭矩轴坐标系下的自由振动微分方程为：

式中，M是系统6阶质量矩阵，由动力总成的质量、转动惯量和惯性积构成，具体计算方法详见文献[10]；K为系统的6阶刚度矩阵，包含每个悬置元件的安装位置、安装角度和刚度，具体计算方法详见文献[10]。

悬置系统的固有频率和模态可由下式求得：

式中，Φ为悬置系统的振型矩阵；ω为相应的振动角频率矩阵。

求解公式（4）即可得到动力总成悬置系统的6阶振动固有频率fi=ωi/2π（i=1，2，...，6）及与之相对应的振型φi。当系统以第i阶固有频率fi和振型φi振动时，第t个广义坐标上分配的动能占系统总动能的百分比（能量解耦率）为[4～6]：

当Tpi=100%时，即表示系统在该阶次振动模态下只存在t方向上的振动。

3 解耦优化实例

某直列4缸发动机（怠速750 r/min）采用3点悬置横置布置，动力总成质量和惯性参数见表1，各悬置安装位置、安装角度分别见表2和表3，各参数值的参考坐标系均为曲轴坐标系。

表1 动力总成质量和惯性参数

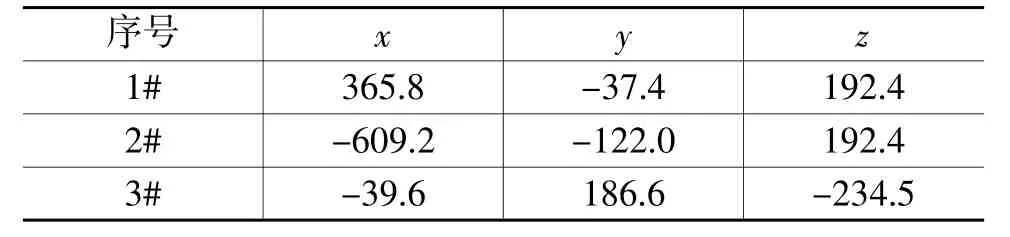
表2 悬置安装位置mm

表3 悬置安装角度（°）

3.1 设计变量

设计化变量通常可取悬置安装位置、安装角度和悬置的3向刚度，由于悬置安装位置和角度受整车布置影响一般很难更改，故此处只取悬置低频段动刚度作为优化变量。为了得到良好的隔振效果，同时能够很好的限制动力总成在相应工况下的位移，取各变量优化空间为[60，400]N/mm。

3.2 设计目标

3.2.1 激励频率

车辆在行驶中受到两个激励：一个来自路面，另一个来自高速运转的发动机及传动系统。路面的激励虽然广阔，但是基本上都属于低频范围，而且是通过悬架系统传递给发动机的，其频率除个别点外，一般是在2.5Hz以下。而来自发动机的激励频率相对高一些，因此进行悬置系统的隔振设计时需要重点对发动机的内部激振频率进行分析。发动机的点火频率：

式中，N为气缸数；n为曲轴转速；τ为冲程数，一般等于4。

3.2.2 频率和解耦率目标值

根据式（6）可求得该发动机最低点火频率为25Hz，根据隔振理论可知，当系统固有频率小于激励频率的时才会起到隔振效果，所以悬置系统的最大振动固有频率必须小于17.5 Hz；最小固有频率应高于半阶次发动机最低点火频率，否则可能导致怠速工况车内抖动严重的现象；发动机最低点火频率与绕曲轴方向的模态频率之比一般在2～3之间；同时还要避开4～7 Hz的人体敏感频率范围。

通常用前后（Fore/after）、左右（Lateral）、上下（Bounce）、侧倾（Roll）、俯仰（Pitch）和横摆（Yaw）来描述动力总成悬置系统的6个振动模态，分别对应整车坐标系的x、y、z、θx、θy和θz6个方向。工程实际中很难实现6个自由度完全解耦，考虑发动机的激励主要是2阶不平衡往复惯性力和绕曲轴方向的扭矩波动，所以该2个方向的解耦率均要求达到90%以上，其它几个方向解耦要求相对较低。通过以上分析，各优化目标要求具体见表4。

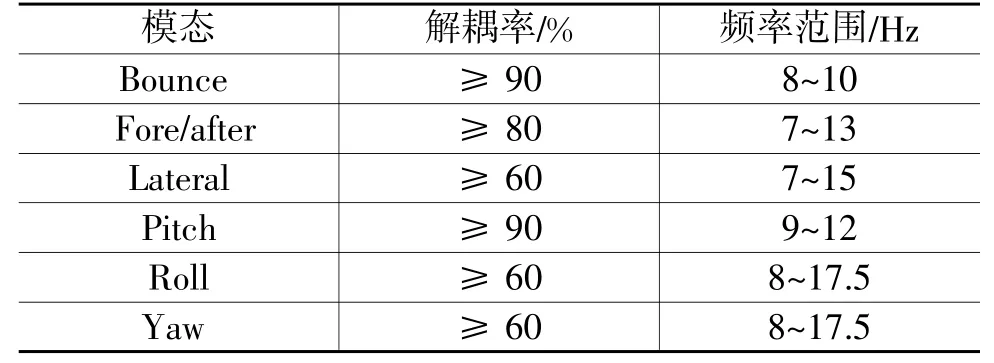
表4 能量解耦设计目标

3.2.3 优化目标函数

对于多目标优化问题，一般通过设置各目标的权重以加权求和为最终优化目标，这样可以将多目标优化问题转化为单一目标的优化问题。由于各解耦率和频率优化目标均为某个区间，可构造如下优化目标函数：

式中，wi为第i个子目标的权重；fi（x）为第i个子目标。

式中，hi（x）为第i阶振动固有频率或解耦率目标；a、b分别为hi（x）的设计下限和上限。

3.3 约束条件

目前的优化设计都未考虑悬置3个主轴向刚度之间的约束关系，因此优化得到的悬置刚度有时是不合理的，或者在结构上由于边界条件等限制而无法实现。本文结合工程实际，在优化时对设计变量施加如下约束：

式中，k表示单个悬置的刚度。

综合考虑橡胶的压缩和剪切刚度比（一般为3～8）以及该款动力总成悬置的结构型式，各悬置3个主轴向刚度之间存在如表5所列的约束关系。

表5 刚度比例约束

3.4 优化算法

汽车动力总成悬置系统能量解耦的数学模型与悬置参数之间的函数关系复杂，存在许多局部最优解[11]。求解该类问题时，传统的优化算法容易陷入局部最优解而使寻优过程停滞不前，而遗传算法（Genetic Algorithm，GA）可以很好的解决该问题。GA作为一种实用、高效、鲁棒性强的优化技术，广泛应用于函数优化、自动控制等领域。通过Matlab提供的遗传算法工具箱函数ga，可以对目标函数进行编程优化计算，其调用格式如下：

[x，fval，exitflag，output]=ga（@optfun，nvars，[]，[]，[]，[]，lb，ub，@confun，options）

其中，x是返回优化得到的设计变量值，fval是返回优化得到的目标函数值，exitflag是返回算法迭代求解终止的原因，output是返回算法迭代求解的相关信息，optfun和confun分别为优化目标函数和约束函数m文件，nvars为设计变量的个数，lb和ub分别为设计变量的取值下限和上限，options为ga函数的结构参数设置选项。

3.5 计算结果

表6为优化前、后各悬置的刚度，表7为优化前悬置系统的固有频率及能量分布情况，表8和表9分别为无约束和有约束优化后悬置系统的固有频率和能量分布情况。

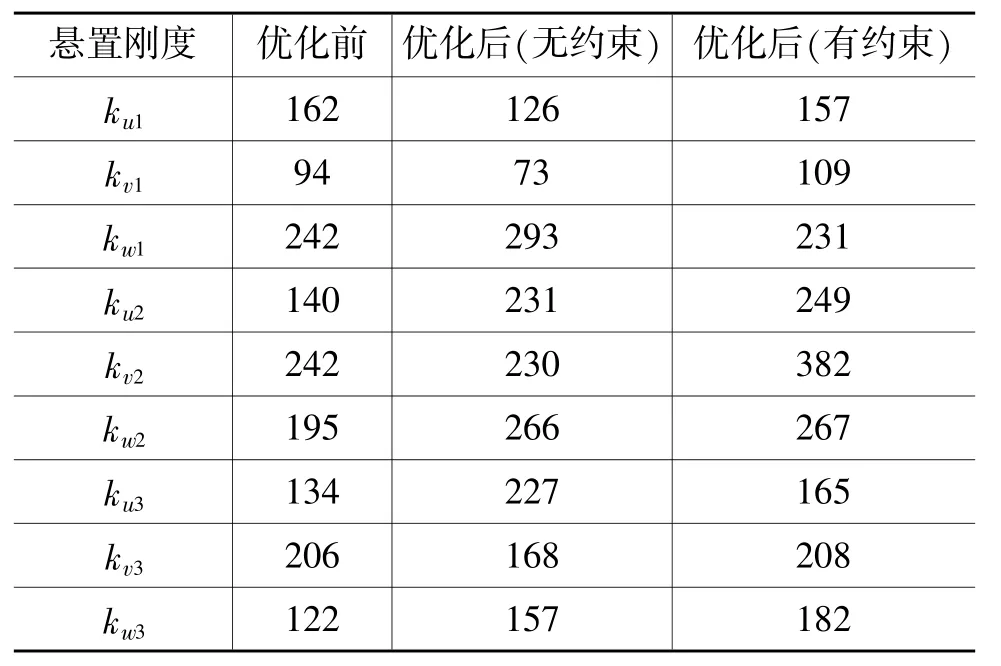
表6 优化前、后悬置刚度N·mm-1

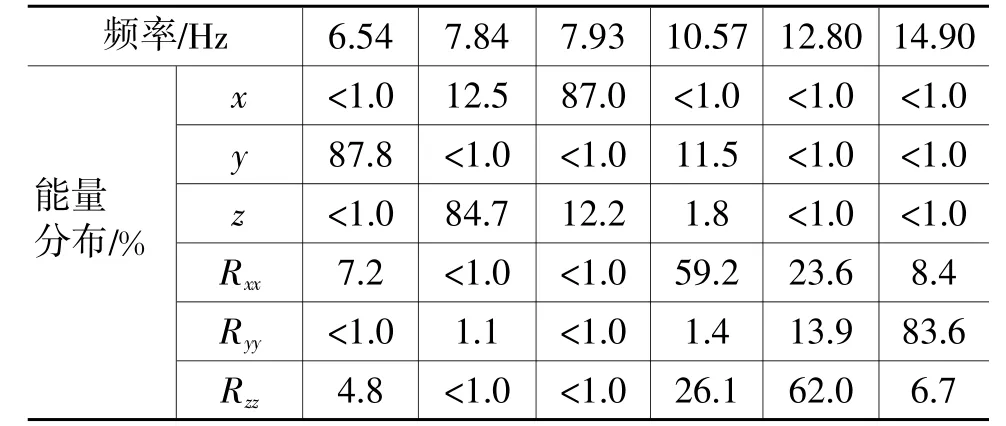
表7 优化前频率和能量分布

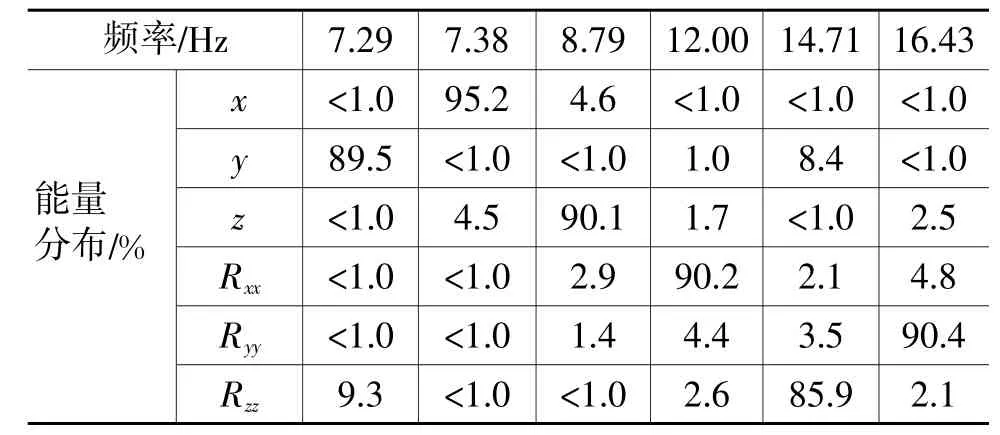
表8 优化后频率和能量分布（无约束）

表9 优化后频率和能量分布（有约束）

对比优化前、后结果可知，优化前悬置系统第1阶振动固有频率偏低，而且Pitch模态（Rxx方向）的解耦很差，优化后各项指标均满足设计目标。另外，对比表8和表9结果可知，无约束优化得到的悬置系统Roll模态（Ryy方向）和Yaw模态（Rzz方向）的解耦均比有约束优化的高，但优化得到的悬置1和悬置3的刚度在结构上无法实现，可见在进行悬置系统的优化设计时，对各悬置刚度比进行约束是很有必要的。

3.6 Adams建模仿真

为了验证所编写的Matlab解耦优化程序的准确性，用机械动力学仿真软件Adams进行悬置系统的动力学仿真分析，其仿真模型如图3所示。

Adams模型里扭矩轴坐标系为大地坐标系，根据式（10）求得曲轴坐标系在扭矩轴坐标系下的欧拉角坐标(ψ，θ，φ)。将扭矩轴坐标系绕自身z轴旋转ψ角，然后绕x轴旋转θ角，最后再绕z轴旋转φ角即可得到曲轴坐标系。然后便可以由曲轴坐标系为参考坐标系设置悬置点位置、安装角度、3向刚度和动力总成转动惯量。

式中，A为扭矩轴坐标系在曲轴坐标系下的方向余弦矩阵；Cψ=cosψ，Sψ=sinψ，其它类同。

Adams仿真分析结果见表10，与表9对比可知，Adams仿真计算结果和Matlab理论计算结果误差很小，从而说明Matlab程序的编写是准确可靠的。

表10 优化后频率和能量分布Adams仿真结果（有约束）

4 稳健性分析

悬置的刚度、安装位置和安装角度由于制造、加工、测量及安装等误差而存在不确定性，因此需要对优化后的设计进行稳健性分析。本文运用蒙特卡罗模拟方法对优化结果进行稳健性分析，悬置刚度在其均值±15%范围内服从正态分布，采样点数取10 000，利用Matlab编写相应计算程序。图4～图7依次为第1阶固有频率、第6阶固有频率、ZT向和绕XT方向解耦率的概率分布情况，从结果（均值mean和标准差std）可知通过该程序优化后悬置系统性能稳健性较好。

5 结束语

建立了悬置系统的6自由度振动分析模型，详细阐述了在扭矩轴坐标系下的固有频率和能量解耦计算方法。以某动力总成悬置系统为计算实例，利用Matlab编写解耦优化程序对该悬置系统进行解耦优化设计，通过对比Adams计算结果，表明所编写的程序是准确可靠的。考虑到悬置刚度的制造、加工误差，运用蒙特卡罗模拟方法，对优化后悬置系统的稳健性进行分析，结果表明，通过该程序优化后悬置系统稳健性较好。另外，由于优化时以悬置某主轴向和另外两个主轴向刚度比为约束条件，使得优化得到的结果符合工程实际情况。

1庞剑，谌刚，何华.汽车噪声与振动_理论与应用.北京:北京理工大学出版社，2006.

2上官文斌，蒋学锋.发动机悬置系统的优化设计.汽车工程，1992（2）:103～110.

3吕振华，罗捷，范让林.汽车动力总成悬置系统隔振设计分析方法.中国机械工程，2003（3）:91～95.

4阎红玉，徐石安.发动机-悬置系统的能量法解耦及优化设计.汽车工程，1993（6）:321～328.

5徐石安.汽车发动机弹性支承隔振的解耦方法.汽车工程，1995，17（4）:198～204.

6叶向好，郝志勇.基于Matlab的发动机总成悬置系统设计研究.小型内燃机与摩托车，2004（5）:12～15.

7M Q，M S，F J.Robustness of powertrain mount system for noise，vibration and harshness at idle.Proceedings of the Institution of Mechanical Engineers，Part D:Journal of Automobile Engineering，2002，216（10）:805～810.

8赵云飞，成艾国，黄清敏，等.田口鲁棒设计用于汽车动力总成悬置系统.计算机仿真，2011（12）:343～347.

9吴杰，上官文斌.基于6σ的动力总成悬置系统鲁棒优化设计.振动与冲击，2008（8）:64～67.

10Taeseok J，Rajendra S.Analytical Methods of Decoupling the Automotive Engine Torque Roll Axis.Journal of Sound and Vibration，2000，234（1）:85～114.

11付江华，史文库，沈志宏，等.基于遗传算法的汽车动力总成悬置系统优化研究.振动与冲击，2010（10）:187～190.

（责任编辑晨曦）

修改稿收到日期为2013年5月1日。

Optimization and Robustness Analysis of Powertrain Mounting System

Tong Donghong，Hao Zhiyong
（Zhejiang University）

To improve the vibration insulation performance of the powertrain mounting system，we use a mounting system as research object and construct a DOF vibration analysis mathematical model in the torque axis coordinate system，and analyze energy decoupling method.The mounting system is optimized with genetic algorithm with vibration decoupling ratios and natural frequencies as design objectives，and dynamic stiffness of individual mount as design variables.Finally，the design robustness is analyzed by using Monte Carlo simulation method.The results illustrate that the decoupling ratios and frequencies meet the design requirements after optimization，and the design robustness is also satisfactory.

Powertrain,Mounting system,Robustness,Energy decoupling

动力总成悬置系统稳健性能量解耦

U461

：A文献标识码：1000-3703（2014）02-0019-05