制造业供应链产销协同计划冲突协商模型

杜同，蒋国瑞

北京工业大学经济与管理学院，北京 100124

制造业供应链产销协同计划冲突协商模型

杜同，蒋国瑞

北京工业大学经济与管理学院，北京 100124

面对市场竞争日益剧烈和客户需求多样化的趋势，制造业供应链的制造商和经销商努力实现产销协同计划。然而在产销协同计划中时常出现冲突，及时有效消解冲突，能提高整个供应链的协作效率，改善供应链上企业间的合作关系；反之，会降低供应链的运作效率，削弱供应链的竞争力。针对这类冲突问题，引入让步协商策略，在有限信息共享条件下，建立供应链产销协同计划冲突协商模型；设计具有历史提议回顾特点的协商流程；通过文化基因算法，产生反提议生成策略；通过算例验证文化基因算法及冲突协商模型的有效性。

冲突消解；让步协商；文化基因算法；制造业供应链；产销协同计划；有限信息共享

1 引言

供应链产销协同包括需求预测、产品设计、生产计划、库存与物流、销售等供应链协同中的核心业务，是制造业每时每刻都在进行的最重要活动[1]。协同计划是产销协同的重要环节。由于各企业追求的目标、价值观以及获得信息的渠道不尽相同，协同计划中往往不可避免地会产生价格、数量和交货时间等决策变量上的冲突[2]。如果不能及时有效地消解冲突，将影响供应链产销协同计划，降低供应链竞争力[3]。

以前供应链产销协同计划的研究，常常假设信息在整个供应链系统上是可以实现完全共享的，一般采用集中式的计划模型来解决企业之间的冲突[4]。然而由于供应链系统组织结构和信息保密的限制，整个供应链系统上的信息完全共享往往难以实现，有限信息共享条件下的协同计划更符合供应链的现实情况，从而成为协同计划研究的重要发展方向[5]。信息不完全也使产销协同计划冲突消解更加复杂。例如，Dudek等针对双边的多产品能力约束批量计划中的冲突问题，利用一种基于多目标规划思想的计划调整策略，通过在协商中反复交换计划方案和成本信息获得相对较优的计划[6]；在此方法基础上，张瀚林等以遗传算法的选择、交叉和变异过程为调整机制，将协商中交流的备选计划及其所产生的成本变化信息融入到计划调整算法中，产生一种具有多点搜索和概率搜索特点的协同计划冲突消解方法[5]；李应等针对具有合作伙伴关系的多级分布式供应链协同计划问题，采用一种基于合作对策的两步协商方法来消解上下游企业之间冲突[7]；戢守峰等将代理机制引入供应链协同计划中，给出一种有限信息共享下基于协同Agent的生产-分销计划模型[4]。

以上研究都假设供应链上企业拥有相同的决策目标（整体收益最优等），在此基础上研究有限信息共享下的产销协同冲突消解问题。然而供应链上企业各自追求收益最大化是更为现实的实际问题，这种情况下的冲突消解是亟需解决的新问题。针对有限信息共享下供应链产销协同计划中的冲突问题，本文假设制造商和经销商都以自身收益最优为决策目标，引入让步协商策略，建立协商模型，设计运行流程，提出基于文化基因算法的反提议生成策略，通过协商消解冲突，达成合作或协作协议，从而实现双赢。

2 产销协同计划数学规划模型

2.1 问题描述及参数定义

考虑供应链下游的制造商和经销商产销协同计划问题。制造商负责生产多种产品，并以批发价格卖给经销商，经销商再以销售价格卖给消费者。假设制造商的产品制造能力、库存能力均存在限制，并且能力上限随周期的改变而变化；假设产品的运输费用包含在销售成本中，由经销商承担；假设经销商每一周期的需求必须被制造商完全满足，不允许缺货[8]。下面定义产销协同计划问题相关的符号。

T为周期；I为产品。

决策变量：

pit为第t周期产品i的销售价格；xit为第t周期产品i的生产量。

状态变量：

ait为0-1变量，反映第t周期产品i是否进行产品制造活动，取0时表示不发生产品制造活动，取1时发生产品制造活动；NIit为第t周期产品i的库存；dit为第t周期产品i的需求量。

相关参数：

NLit为第t周期产品i的制造能力上限；NSLt为第t周期产品库存能力上限；PULit为第t周期产品i的销售价格上限；PCit为第t周期产品i的单位制造成本；PSCit为第t周期产品i的单位库存成本；MCit为第t周期产品i的单位销售成本；WPit为第t周期产品i的批发价格；UISi为单位产品i所占的库存；SPCi为产品i制造活动的生产准备成本；γt为第t周期经销商所分担的库存成本的比例；B为大常数。

2.2 数学规划模型

假设产品i需求：dit=αi-βipit，其中，αi，βi都是大于零的常数。αi是市场容量，βi是价格敏感系数。则制造商与经销商的数学规划模型如下：

I制造商收益=产品批发收入-可变生产成本-固定生产成本-制造商承担库存成本，表达式为：

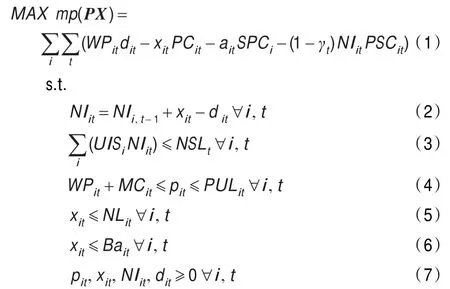
II经销商收益=产品销售收入-产品订购成本-销售成本-经销商承担库存成本，表达式为：

其中，mp(PX)与rp(PX)分别是制造商和经销商的收益函数，PX是由全部决策变量组成的向量；式（2）表示产品库存平衡；式（3）表示产品库存能力约束；式（4）表示价格取值约束；式（5）表示产品制造能力约束；式（6）确保式ait∈{0，1}；式（7）表示非零约束。令计划开始时产品的库存为零，即NIi，0=0。

3 产销协同计划冲突协商模型

3.1 协商描述与假设

协商双方分别为协商发起者与协商接受者，每轮协商中，协商发起者先发出提议，协商接受者评价后发出反提议，然后协商发起者评价反提议并在下一轮提出新提议[9]。另对协商作出如下假设：

假设1制造商和经销商是平等的，不存在中间协调者。

假设2制造商和经销商是理性的，以自身收益最大化为目标。

假设3制造商和经销商只共享有限信息。本文中库存成本、能力约束、产品需求函数以及库存成本分摊比例为共享信息，其他信息为私有信息。

假设4协商失败对于制造商和经销商而言都是不好的结果。

3.2 协商模型

协商模型可以描述为一个十元组：NM=＜S，B，IS，fs(IS)，fb(IS)，hs(r)，hb(r)，CX，R，NR＞。其中，S，B分别表示协商发起者和协商接受者；IS={is1，is2，…，isn}为协商议题集合，本文以协同计划问题的决策变量为协商议题，fs(IS)与fb(IS)分别表示S与B的收益函数；hs(r)，hb(r)分别表示S与B的让步函数；CX为协商的可行方案集合（可行域），CX中的所有方案必须满足式（2）～（7）的约束；R表示最大协商轮次；NR={N1，N2，…，NR}，Nr表示第r轮协商中交互提议的数目。

另外，为方便描述协商流程，令MSD、MBD分别表示可行域内使S与B收益最大的提议；SPSrk与BPSrk分别表示S和B第r轮提出的提议方案中的第k个提议，r=1，2，…，R，k=1，2，…，Nr；sp，bps分别表示SPSrk与BPSrk的第l个议题。

3.3 协商流程

协商开始时需要检测协商双方是否存在冲突，具体方法是：协商双方交互最大收益提议MSD、MBD，若两者相等，说明冲突不存在，以MSD为协商结果，协商结束。若两者不相等，说明冲突存在，需要通过协商来消解冲突，随机选择两者之一为协商发起者，进入协商过程。协商流程如图1所示。

图1 双方交互过程中的协商流程

每轮协商中，协商参与者都需要计算本轮让步区间。本文将让步区间划分为与最大协商轮次R相关的若干子让步区间，区间之间不重叠，前一让步区间的下限即为后一让步区间上限，区间内利用文化基因算法搜索有效提议，实现搜索区间的全覆盖。令第r轮协商发起者的让步下限为SLr，让步上限为SUr，则

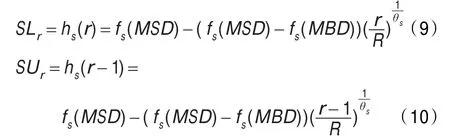
其中θs是决定协商发起者让步函数形状的参数。当协商发起者让步到fs(MBD)时，可以直接接受MBD作为协商结果，而MBD必然会被协商接受者所接受，所以没有再继续协商的必要。相应的，记第r轮协商接受者的让步下限为BLr，让步上限为BUr，协商接受者让步函数：

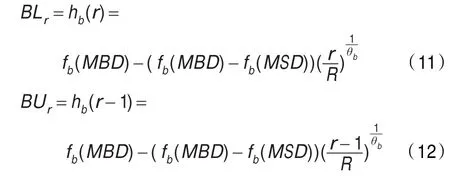
其中θb是决定协商接受者让步函数形状的参数。首轮协商开始时，协商发起者直接计算首轮让步区间，生成并向对方发送首轮提议。由于没有历史提议，首轮协商中，协商双方无需回顾历史提议。除首轮外，协商参与者每次作出让步后先要回顾对方提出的所有提议，若发现其中最优提议的收益已经不小于当前的让步区间下限，则以之为协商结果，协商结束；否则协商参与者生成反提议发送给对方。对方收到反提议方案后，若发现其中最优提议的收益不小于让步下限，则以该提议为协商结果，协商结束；否则，执行更改让步区间，回顾历史提议，生成反提议等过程。如果直到第R轮协商结束，双方仍没有达成一致，则以MSD为协商结果，协商结束。

3.4 反提议生成策略

协商参与者若不接受对方提出的提议，可以提出反提议，反提议生成策略如下：在第r轮协商中，协商参与者利用文化基因算法求解反提议生成模型，从算法最后一代种群中选出前Nr个最优个体，组成反提议方案发送给对方。记XD表示待评价提议，xdl表示其第l个议题。以相似度最大化为目标构造反提议生成模型，第r轮协商发起者反提议生成模型如下：

III协商发起者反提议相似度=反提议与协商接受者各提议相似度之和/提议数目

采用向量夹角余弦法计算相似度，gs是协商发起者的反提议相似度函数；式（14）表示让步区间约束，式（15）表示可行域约束。与模型III相似，第r轮协商接受者的反提议生成数学模型如下：

IV协商接受者反提议相似度=反提议与协商发起者各提议相似度之和/提议数目

gb是协商接受者的反提议相似度函数；式（17）表示让步区间约束；式（18）表示可行域约束。

4 冲突协商模型求解算法

4.1 文化基因算法流程

本文利用文化基因算法求解模型III、IV，生成反提议。1989年，Moscato以达尔文自然进化理论与道金斯文化进化理论为基础，首先提出文化基因算法（Memetic Algorithm）的概念[10]。文化基因算法是一种求解大规模复杂优化问题的有效方法[11]，已经被广泛应用到图像处理[12]、生产计划[13]、网络分布设计[14]等多个领域，但尚未有人将其应用到自动协商中。本文以自适应遗传算法为全局搜索算法，以Powell算法为局部搜索算法，算法基本流程如图2所示。

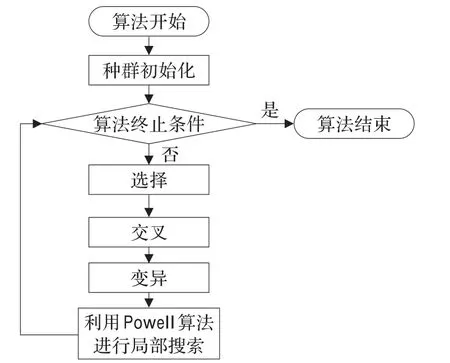
图2 文化基因算法流程

4.2 文化基因算法的局部搜索

局部搜索过程发生在进化操作之后。因为基本的Powell算法具有二次终止性，所以本文采用一种改进算法，算法具体流程如下[15]：

步骤1取初始点x(1)，置n个线性无关的方向d(1)，d(2)，…，d(n)，置精度要求为ε，搜索代数k=1，最大搜索代数为K。

步骤2对于i=1，2，…，n，令f表示适应度函数，求解一维问题：

4.3 文化基因算法的全局搜索

本文全局搜索算法是一种自适应遗传算法，算法具体如下。

编码：采用二进制编码方式，令[lbi，ubi]表示议题i的取值范围，lb′i表示不大于lbi的最大整数，ub′i表示不小于ubi的最小整数。用二进制表示议题i的值，二进制码长度为NIi+MIi，NIi是ub′i-lb′i对应的二进制代码长度，MIi是精度要求，表示算法执行过程中精确到1/2MIi；将所有议题的二进制码串联起来即构成一个染色体。因此染色体的长度CHL=∑NIi+MIi，如图3所示。

图3 编码示意图

种群初始化：以随机的方式生成初始种群。

适应度函数：交互协商中，以反提议相似度函数为算法的适应度函数。

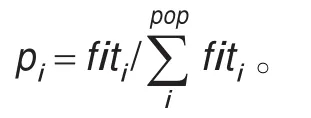
交叉算法：采用最简单的单点交叉方式，交叉点随机选取；交叉概率随父代适应度自动变化，且具有非线性变化的特性，自适应的交叉概率：

表1 三个周期数值参数选择

表2 两种产品数值参数选择

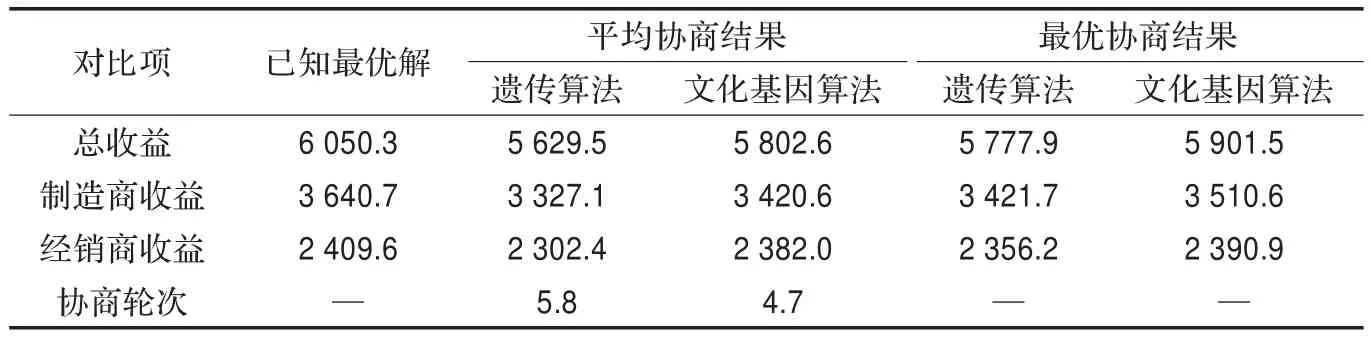
表3 两种算法的协商结果比较

其中，fitmax是种群中最优秀个体的适应值；fitavg是每代种群的平均适应度值；fit′是交叉的两个个体中较优秀的适应值；pcmax及pcmin分别表示交叉率值的上、下限，λc是一固定常数。

变异算法：通过变异引入新基因可以保持种群多样性，并在一定程度上避免早熟，随机选取变异位置，非线性变化的变异概率：

其中，pmmax及pmmin分别表示变异率值的上、下限，λm是一固定常数。fit″是变异个体的适应值。

5 实验

考虑供应链在三个计划周期内销售两种产品的产销协同计划问题，数值实验的具体参数如表1～表2所示。表1是不同周期供应链成本与能力限制参数，表2是有关产品销售、产品库存、生产准备成本的参数。

以制造商为协商发起者，最大协商轮次R=10，制造商与经销商的让步形状参数θs与θb分别为2与1.5，Nr=2。

文化基因算法的参数方案如下：Powell算法的最大迭代代数为50，精度要求为0.01，随机选择12个线性无关的初始方向；自适应遗传算法的种群规模为20，最大进化代数50，初始化、选择、交叉、变异过程如4.3节所述。为了验证文化基因算法的有效性，本文还利用遗传算法求解冲突协商模型，遗传算法的参数方案如下：采用二进制编码方式，随机生成初始种群，种群规模20，最大进化代数50；采用轮盘赌选择方法，单点交叉，交叉率0.8，单点变异，变异率0.05。两种算法中制造商与经销商都以反提议相似度函数作为适应度函数。

利用Matlab平台对协商过程进行编程实现。协商前利用MATLAB，以总收益最大化为目标求得该供应链协同计划问题的最优解：制造商收益3 640.7，经销商收益2 409.6，总收益6 050.3。

两种算法的协商程序在Intel Pentium Dual T3200，2.00 GHz，2 GB内存的计算机上各自独立运行30次，协商结果如表3。

实验结果分析及结论：将两种算法的协商结果进行比较，发现文化基因算法明显优于遗传算法。利用文化基因算法进行协商可以通过较少的协商轮次获得更加接近最优解的协商结果。

将基于文化基因算法的协商结果与最优解相比较，发现协商结果已经十分接近最优解。平均制造商收益、平均零售商收益、平均供应链总收益与已知最优解的差距不超过7%；最优制造商收益、最优零售商收益、最优供应链总收益与已知最优解的差距均不超过4%；而且协商达成一致所需轮次平均不足最大协商轮次的50%。

6 结束语

供应链产销协同计划包含供应链协同大量的核心业务，有效地消解产销协同计划中的冲突，对于提高供应链运行效率具有重要意义。本文将让步协商策略引入产销协同计划冲突消解中，针对下游企业决策冲突的问题，建立协商模型，在协商流程中加入历史提议回顾过程，加快协商达成一致的进程，利用文化基因算法寻优能力强的优势，搜索有效反提议。实验结果表明文化基因算法比遗传算法更有效，基于文化基因算法的冲突协商模型可以使供应链上的企业在共享有限信息的情况下，通过较少的交互轮次获得接近最优解的决策。

[1]Maxime O，van Dat C，Julien B，et al.Decentralised planning coordination with quantity discount contract in a divergent supply chain[J].International Journal of Production Research，2013，51（9）：2776-2789.

[2]Shima M，Li Xueping.Designing intelligent agents to support long-term partnership in two echelon e-supply networks[J].Expert Systems with Applications，2012，39（18）：13501-13508.

[3]蒋国瑞，段晓敏，张瀚林.基于冲突检测的供应链协同计划[J].计算机工程，2010，36（3）：247-249.

[4]戢守峰，张吉善，张川，等.基于代理的分散式生产—分销系统协同计划模型[J].计算机集成制造系统，2010，16（4）：822-827.

[5]张瀚林，蒋国瑞，黄梯云.一种有限信息共享的全局寻优供应链双边协同计划方法[J].管理工程学报，2010，24（2）：153-158.

[6]Dudek G，Stadtler H.Negotiation-based collaborative planning in divergent two-tier supply chains[J].International Journal of Production Research，2007，45（2）：465-484.

[7]李应.供应链多层规划问题及其合作对策协商求解[J].运筹与管理，2012，21（4）：52-58.

[8]Zhang Jian，Liu Xiao，Tu Y L.A capacitated production planning problem for closed-loop supply chain with remanufacturing[J].International Journal of Advanced Manufacturing Technology，2011，54（5）：757-766.

[9]Lai G，Sycara K，Li C.A decentralized model for automated multi-attribute negotiations with incomplete information and general utility functions[J].Multiagent Grid System，2008，4：45-65.

[10]Raúl B，Consolación G，Juan R，et al.A pareto-based memetic algorithm for optimization of looped water distribution systems[J].Engineering Optimization，2010，42（3）：223-240.

[11]Saman P M，Zanjirani F R，Wout D.A memetic algorithm for bi-objective integrated forward/reverse logistics network design[J].Computers and Operations Research，2010，37（6）：1100-1112.

[12]Sharif K M，Mohamad A A F，Amitay I，et al.A smart repair embedded memetic algorithm for 2D shape matching problems[J].Engineering Optimization，2012，44（10）：1229-1243.

[13]Schemeleva K，Delorme X，Dolgui A，et al.Multi-product sequencing and lot-sizing under uncertainties：a memetic algorithm[J].Engineering Applications of Artificial Intelligence，2012，25（8）：1598-1610.

[14]Raúl B，Consolación G，Juan R，et al.A memetic algorithm applied to the design of water distribution networks[J].Applied Soft Computing Journal，2010，10（1）：261-266.

[15]薛毅.最优化原理与方法[M].北京：北京工业大学出版社，2004.

DU Tong,JIANG Guorui

School of Economics and Management,Beijing University of Technology,Beijing 100124,China

In the face of increasingly fierce market competition and increasingly diversified demand,manufacturers and dealers of manufacturing supply chain pay great effort to achieve production marketing collaborative planning.However, it often generates conflicts in the process of production marketing collaborative planning.Resolving conflicts timely and effectively can enhance collaboration efficiency of the whole supply chain and improve cooperation relations between the enterprises in the supply chain.Whereas it will reduce operational efficiency of the supply chain and weaken competitiveness of supply chain.For this kind of conflict problem,concession negotiation strategy is introduced and a conflict negotiation model for supply chain production marketing collaborative planning is built in the case of limited information shared.The negotiation process has the feature of reviewing history proposals.A strategy for generating counter proposals is presented by memetic algorithm.The validity of memetic algorithm and the conflict negotiation model is verified by numerical experimentations.

conflict resolution;concession negotiation;memetic algorithm;manufacturing supply chain;production marketing collaborative planning;limited information shared

A

TP311

10.3778/j.issn.1002-8331.1309-0511

DU Tong,JIANG Guorui.Conflict negotiation model for production marketing collaborative planning in manufacturing supply chain.Computer Engineering and Applications,2014,50（6）：265-270.

国家自然科学基金（No.71371018）。

杜同（1989—），男，硕士，研究领域为商务智能谈判，供应链管理；蒋国瑞（1954—），男，博士，教授，研究领域为管理信息系统，商务智能谈判，智能化供应链管理。E-mail：jianggr@bjut.edu.cn

2013-10-08

2013-12-26

1002-8331（2014）06-0265-06