量子门线路神经网络及其改进学习算法研究

侯旋

西北工业大学电子信息学院，西安 710071

量子门线路神经网络及其改进学习算法研究

侯旋

西北工业大学电子信息学院，西安 710071

量子门线路神经网络（QGCNN）是一种直接利用量子理论设计神经网络拓扑结构或训练算法的量子神经网络模型。动量更新是在神经网络的权值更新中加入动量，在改变权值向量的同时提供一个特定的惯量，从而避免权值向量在网络训练过程中持续振荡。在基本的量子门线路神经网络的学习算法中引入动量更新原理，提出了一种具有动量更新的量子门线路网络算法（QGCMA）。研究表明，QGCMA保持了网络100%的收敛率，同时，相对于基本算法，在具有相同学习速率的情况下，提高了网络的收敛速度。

量子神经网络；量子计算；量子门；动量更新；学习算法；权值

1 引言

人工神经网络（Artificial Neural Network），也称为神经网络（Neural Network，NN），或称为连接模型（Connectionist Model），它是一种模仿动物神经网络行为特征，进行分布式并行信息处理的算法数学模型。这种网络依靠系统的复杂程度，通过调整内部大量节点之间相互连接的关系，从而达到处理信息的目的[1-3]。人工神经网络是通过直观性思维方式模拟人的思维，是一种非线性动力学系统，将分布式存储的信息综合起来，在忽然间产生想法或解决问题的办法。这种思维方式的根本之点在于信息是通过神经元上的兴奋模式分布在网络上，并且通过神经元之间同时相互作用的动态过程完成信息处理[4-7]。人工神经网络技术与量子计算相结合，是一个具有开拓性的尝试。量子计算采用一种与传统的计算方式截然不同的新型计算方法，量子并行处理极大地提高了量子计算的效率，使其达到常规计算技术不能达到的解题速度，还可以解决常规计算不能解决的某些计算复杂度很高的问题。量子计算与传统意义上的计算存在质的不同，量子计算源于对传统计算进行量子改造，而神经计算是对生物行为以信息处理方式进行模拟，若将神经计算推广到量子领域，就有可能利用到量子计算的强大能力[8-12]。同时，神经网络的动力学特征与量子系统之间存在着诸多类似之处，神经网络与量子理论相结合，从而构建量子神经计算（Quantum Neural Computation），以及一种全新的神经计算模型，即量子神经网络（Quantum Neural Network，QNN），它是人工神经网络研究的重要前沿课题[10，12-17]，同时它也是未来人工智能发展的新热点。

量子神经网络是由量子物理学与数学、计算机科学、信息科学、认知科学、复杂性科学等多学科交叉形成的、全新的研究领域[18-20]。量子神经网络是经典神经网络与量子计算结合而产生的一种新的计算范式，其研究原因有两个，一方面大量研究表明人脑存在量子效应，并且量子效应在人脑中具有重要作用；另一方面由于量子理论是经典物理发展到微观层次的产物，因此它具有更普遍、更本质的特征。对量子神经网络的研究，主要包括两个方面[21-26]：一是在经典神经网络的结构或训练过程中引入量子理论，提高神经网络的学习和推广能力；二是直接借用量子理论中的某些原理或概念，指导设计神经网络拓扑结构或训练算法形成新的量子神经网络模型。

2 基本量子门

在量子力学中，量子门通过对量子位进行一系列酉变换，以实现相应的逻辑功能。由通用量子门可以组合成任意的量子门，而最基本的通用量子门是由一位相移门和两位受控非门组成。

2.1 一位相移门

一位相移门的作用是完成相位移动，它可以定义为：

2.2 受控非门

2.2.1 量子非门

量子非门（即Pauli-X门）的作用是交换一个量子位的两个概率幅，可以定义为：

2.2.2 两位受控非门

在量子计算中，可由一位量子门构成任意位量子门。由量子非门σX可构成两位受控非门C2qubit-NOT：

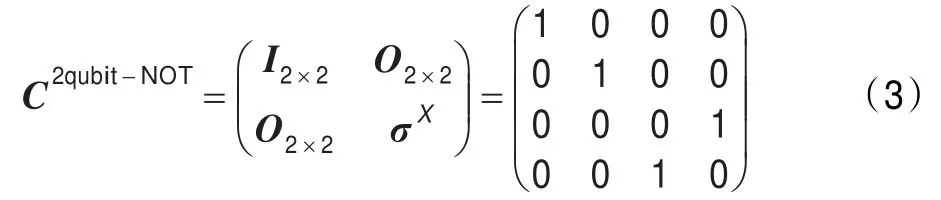
其中I为单位矩阵，O为零矩阵。C2qubit-NOT的作用是当一个双量子比特通过该量子门时，且第一个量子位处于态时，第二个量子位进行翻转。

2.2.3 n位受控非门

由量子非门σX可构成n位受控非门Cnqubit-NOT：

其作用是当一个n量子比特通过该量子门，且前n-1个量子位处于态时，第n个量子位进行翻转。

3 量子门线路网络

3.1 网络模型

量子门线路神经网络（QGCNN）分为三层，即输入层、隐层、输出层，如图1所示，主要参数包括：

图1 量子门线路神经网络模型

（10）目标空间t=(t1t2…ts)。其中目标向量ti=(ti1ti2…tim)T。

3.2 权值更新

QGCNN是直接基于量子门构造的神经网络，它不直接存在经典神经网络或基于经典神经元构造的量子神经网络中的连接权值，这种经典的连接矩阵在量子门线路网络中可以被近似地认为是两个量子门矩阵U(ω)和U(γ)，因此权值更新可被认为是更新这两个矩阵中对应的角度参数ω和γ。

通过网络的目标输出ti和实际输出ai定义误差函数为：

利用梯度下降法计算角度梯度：

其中α为学习速率。

4 改进的量子门线路学习算法

4.1 动量更新

在神经网络的权值更新中加入动量的目的在于改变权值向量的同时，提供一个特定的惯量（即动量），从而避免权值向量在网络训练过程中持续振荡，以提高网络的收敛性能。加入动量的方法是在权值更新中添加一个动量项，权值向量w的动量项可以表示为当前时刻的权值向量w(k)与前其一时刻w(k-1)的权值差异：

其中0＜η＜1为动量参数。

4.2 具有动量更新的量子门线路网络学习算法

步骤1实值样本的量子态描述

步骤2初始化

（1）初始化隐层量子门矩阵U(ω)：

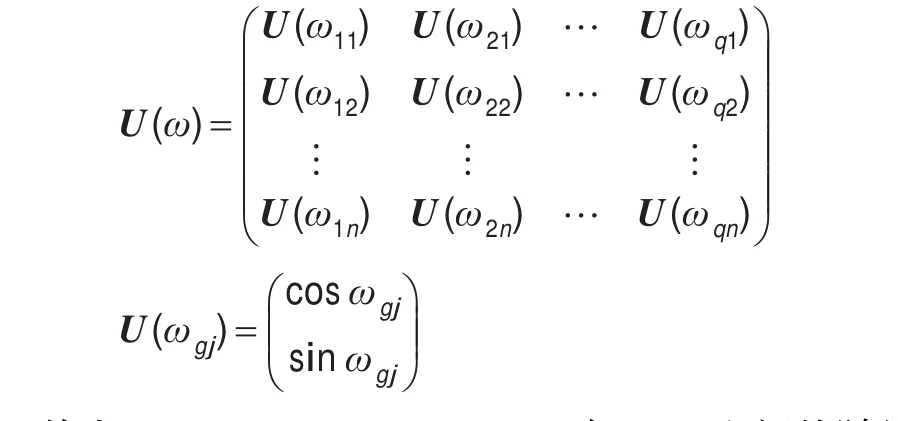
其中ω=2π·random，random为[0，1]之间的随机数。

（2）初始化输出层量子门矩阵U(γ)：

其中γ=2π·random，random为[0，1]之间的随机数。

（3）设置最大循环次数max、循环次数计数k=1、学习速率α、动量参数η。

步骤3若没有达到指定的循环次数，或循环次数计数k小于所设定的最大循环次数max，即k＜max，则继续执行步骤4；若达到指定的循环次数，或循环次数计数k等于所设定的最大循环次数max，即k=max，则结束训练，退出。

步骤4计算隐层的量子输出和实值输出：

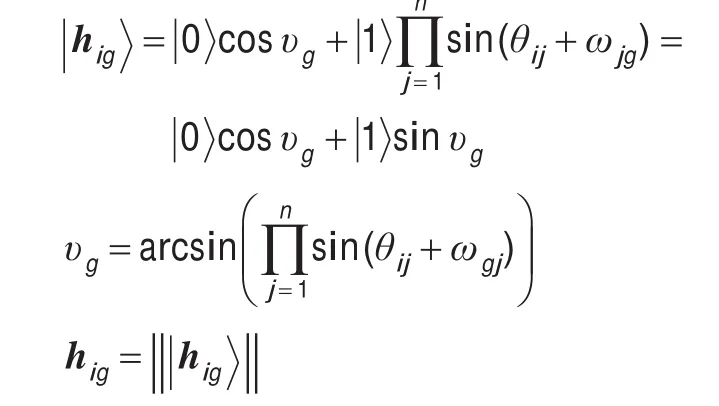
步骤5计算输出层的量子输出和实值输出：

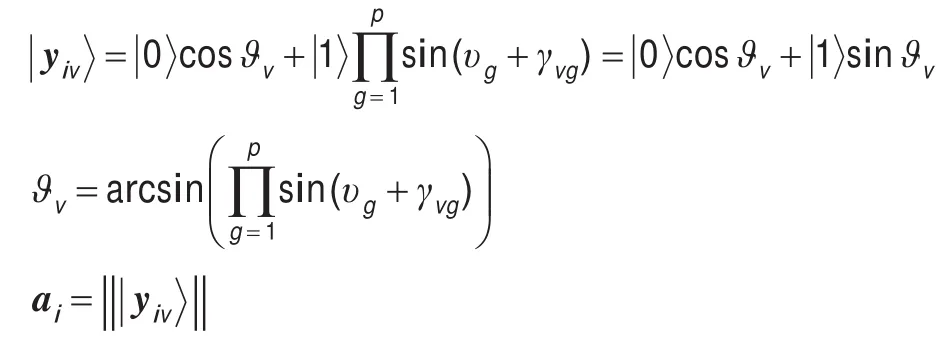
步骤6对隐层和输出层进行权值更新后返回步骤3：

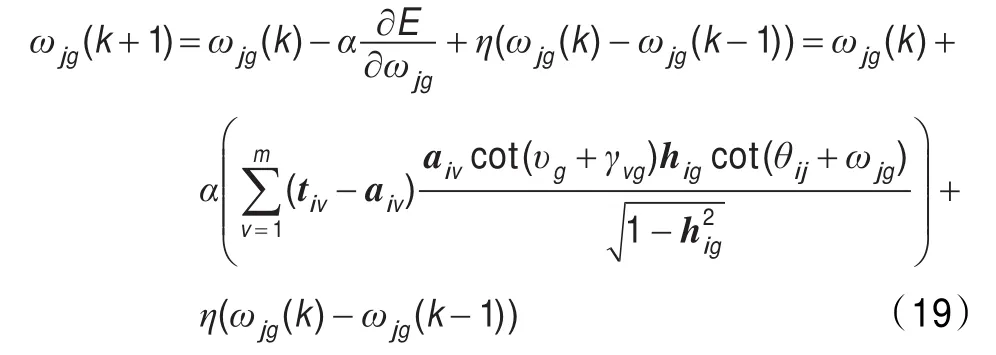
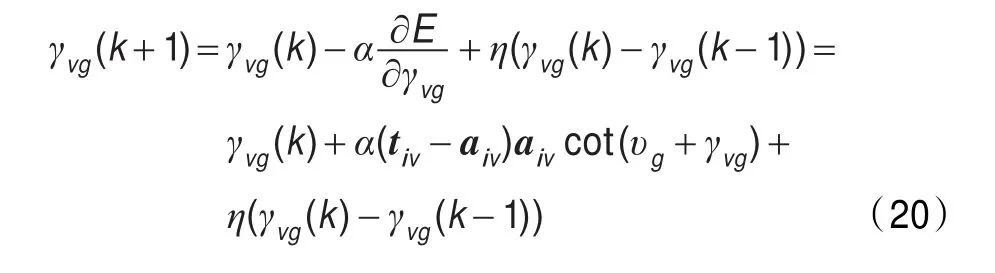
5 性能比较

通过对模式识别问题的研究，对量子门线路网络的基本算法和改进算法进行对比。利用Iris数据集建立一组二维训练样本，将其分为三类，共150个数据，前120个数据作为训练样本，如图2所示，后30个数据作为测试样本，如图3所示。QGCNN输入层神经元个数为2，隐层量子门矩阵为2×10矩阵，输出层量子门矩阵为10×3矩阵，循环计数初始值k=1。

图2 Iris数据-训练样本

图3 Iris数据-测试样本

（1）动量参数η与学习速率α变化对收敛率的影响：

设置两种算法最大循环次数为max=20，学习速率α取值为0.1、0.2、…、0.9、1，QGCMA中的动量参数η取值为0.1、0.2、…、0.9、1，利用Iris数据集训练样本，通过两种算法分别对网络进行训练，如图4所示，基本算法具有100%的网络收敛率；如图5所示，QGCMA也保持了100%的网络收敛率。

（2）学习速率α、动量参数η的变化对网络训练循环次数k的影响：

图4 基本算法学习速率α与收敛率的关系

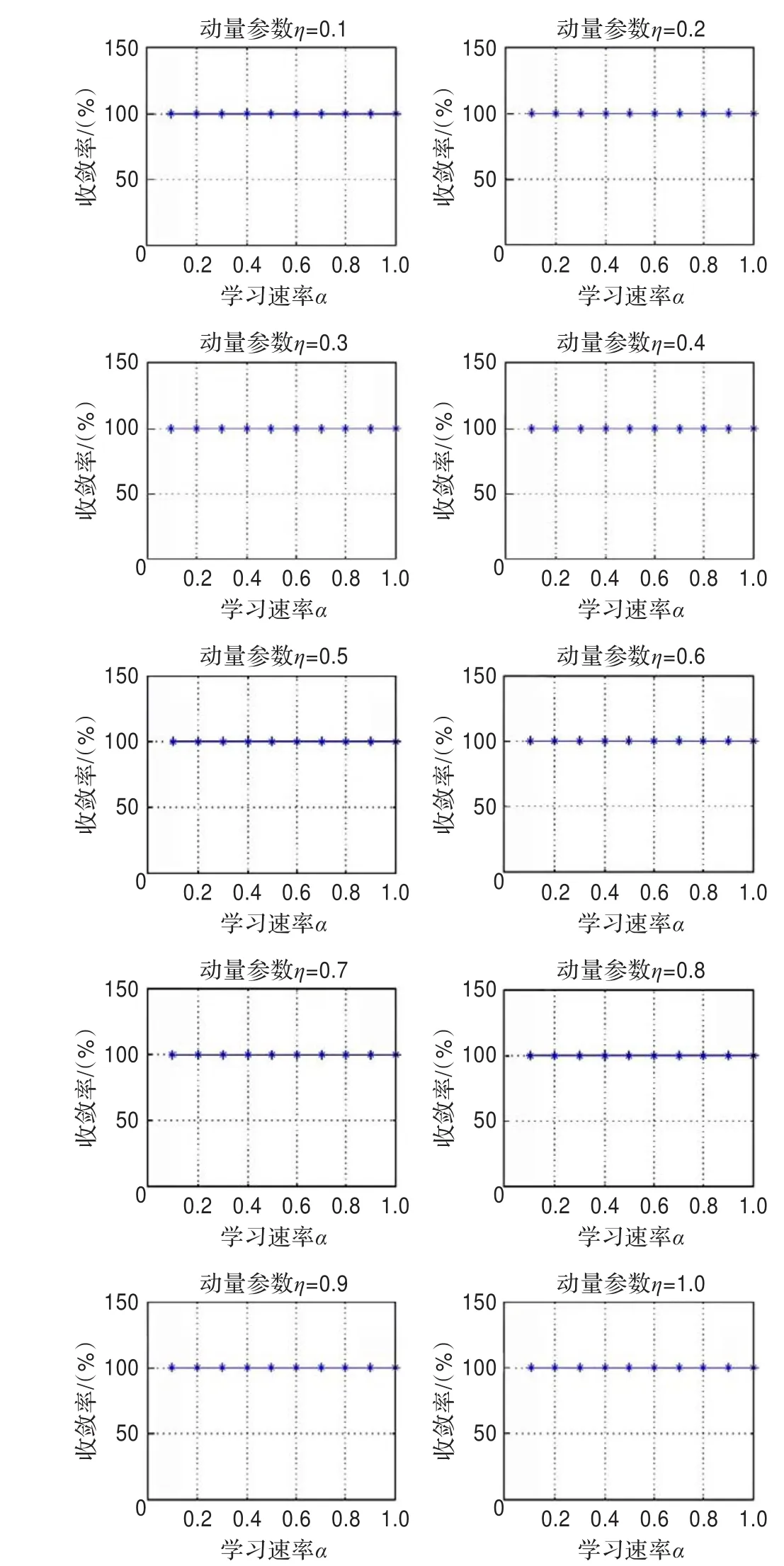
图5 QGCMA学习速率α、动量参数η与收敛率的关系

设置误差精度为0.1，学习速率α取值为0.1、0.2、…、0.9、1，QGCMA中的动量参数η取值为0.1、0.2、…、0.9、1，利用Iris数据集训练样本，通过两种算法分别对网络进行训练。由表1可知，在确定误差精度的情况下，网络训练次数k在η=0.5、α=0.9时达到最优，k获得最小值为3。如图6所示，两种算法在训练时，基本算法达到误差精度所需训练的循环次数k最大值为8，最小值为5；QGCMA在η=0.5的情况下，达到误差精度所需训练的循环次数k最大值为8，最小值为3。结果表明，QGCMA在η取值为0.3、0.4、0.5、0.6、0.7时性能优于基本算法。

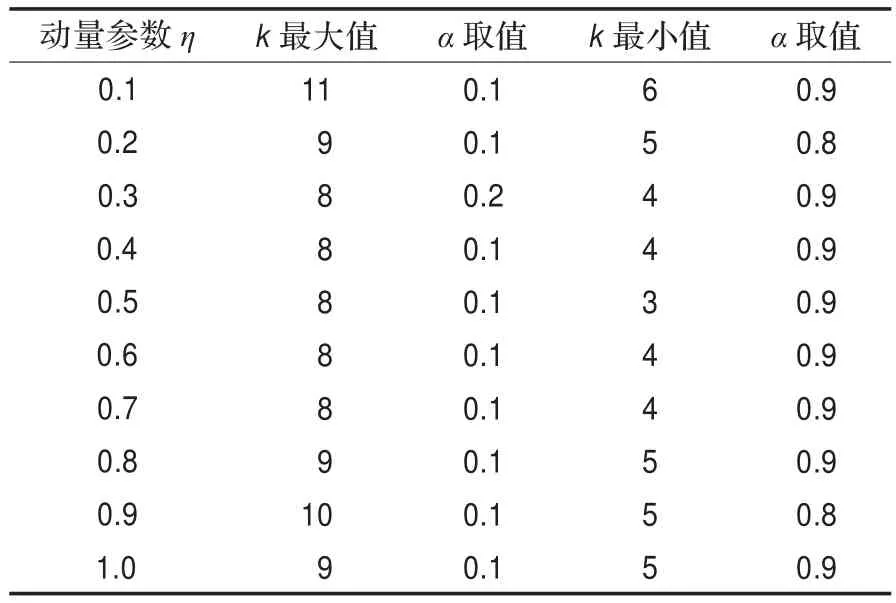
表1 QGCMA中α、η与k的关系

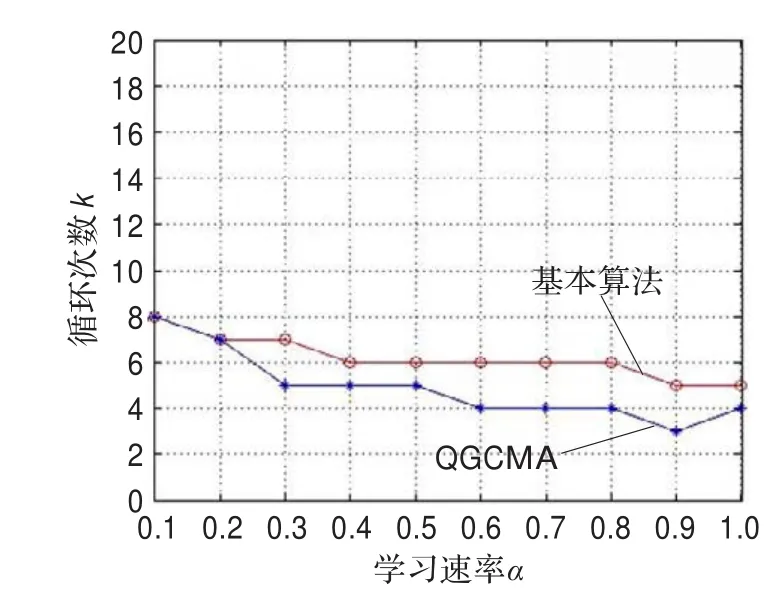
图6 学习速率α与网络训练循环次数k的关系(η=0.5)

6 结束语

量子门线路神经网络（QGCNN）是一种直接利用量子理论设计神经网络拓扑结构或训练算法的量子神经网络模型。在基本的量子门线路神经网络的学习算法中引入动量更新原理，提出了一种具有动量更新的量子门线路网络算法（QGCMA）。研究表明，QGCMA保持了100%的网络收敛率，同时，相对于基本算法，在具有相同学习速率的情况下，提高了网络的收敛速度。

[1]Rabunal J R，Dorado J.Artificial neural networks in reallife applications[M].[S.l.]：Idea Group Publishing，2005.

[2]Gupta S，Zia R K P.Quantum neural networks[J].Journal of Computer and System Science，2001，63：355-383.

[3]Narayanan A，Menneer T.Quantum artificial neural network architectures and components[J].Information Sciences，2000，128：231-255.

[4]Griffiths D J.量子力学概论[M].英文版，原书第2版.北京：机械工业出版社，2007.

[5]Dirac P A M.量子力学原理[M].英文版，第4版.北京：科学出版社，2008.

[6]Jain A K，Duin R P W，Mao Jianchang.Statistical pattern recognition：a review[J].IEEE Transactions on Pattern Analysis and Machine Intelligence，2000，22：4-33.

[7]Ventura D.Quantum computing and neural information processing[J].Information Sciences，2000，128：147-148.

[8]Kak S.Quantum neural computing[J].Advances in Imaging and Electron Physics，1995，94：259-313.

[9]Ezhov A A，Ventur A D.Quantum nerual networks[M]// Kasabov N.Future Directions for Intellgent Systems and Information Sciences.Heidelberg：Springer-Verlag，2000.

[10]Kak S.On quantum neural computing[J].Information Sciences，1995，83：143-160.

[11]Gopathy P，Nicolaos B，Karayiannnis N B.Quantum neural network computes entanglement[J].IEEE Transactions on Neural Network，1997，8（3）：679-693.

[12]Duda R O，Hart P E.Pattern classification and scene analysis[M].New York：John Wiley&Sons，1973.

[13]Hughes G F.On the mean accuracy of statistical pattern recognizers[J].IEEE Trans on Information Theory，1968，14（1）.

[14]Amari S.Mathematical theory of neural learning[J].New Generation Computing，1991，8：281-294.

[15]李盼池，宋考平，杨二龙.基于受控旋转门的量子神经网络模型算法及应用[J].控制与决策，2011，26（6）：898-901.

[16]郭光灿.量子信息技术[J].重庆邮电大学学报：自然科学版，2010，22（5）：521-525.

[17]Hagan M T，Demuth H B，beale M H.神经网络设计[M].戴葵，译.北京：机械工业出版社，2006.

[18]Ham F M，Kostanic I.神经计算原理[M].叶世伟，王海娟，译.北京：机械工业出版社，2007.

[19]周日贵.量子神经网络模型研究[D].南京：南京航空航天大学，2008.

[20]李士勇，李盼池.量子计算与量子优化算法[M].哈尔滨：哈尔滨工业大学出版社，2009.

[21]张贤达.矩阵分析与应用[M].北京：清华大学出版社，2004.

[22]Leon S J.线性代数[M].张文博，张丽静，译.北京：机械工业出版社，2008.

[23]Nielsen M A，Chuang I L.量子计算和量子信息（一）——量子计算部分[M].赵千川，译.北京：清华大学出版社，2004.

[24]Nielsen M A，Chuang I L.量子计算和量子信息（二）——量子信息部分[M].郑大钟，赵千川，译.北京：清华大学出版社，2004.

[25]钟艳花，余永权，余晓敏.量子神经动力学分析[J].量子电子学报，2005，22（2）：192-195.

[26]周树德，王岩，孙增圻，等.量子神经网络[C]//2003中国智能自动化会议论文集（上），北京，2003：163-168.

HOU Xuan

School of Electronics and Information,Northwestern Polytechnical University,Xi’an 710071,China

Quantum Gate Circuit Neural Network（QGCNN）is a kind of quantum neural network model,which directly uses quantum theory to design the neural network topology or training algorithms.In the neural network,Momentum update is adding momentum parameter in weight renew and provides a specific inertia while renewing weight vector.It avoids sustained oscillation of weight vector in network training.It introduces the principle of momentum update in the basic learning algorithm of Quantum Gate Circuit Neural Network,proposes Quantum Gate Circuit neural network Momentum update Algorithm（QGCMA）.The research shows that QGCMA has 100%convergence rate and enhances convergence speed compared to the basic algorithm with the same learning rate.

Quantum Neural Network（QNN）;quantum computation;quantum gate;momentum update;learning algorithm;weight

A

TP391.4

10.3778/j.issn.1002-8331.1205-0249

HOU Xuan.Research on quantum gate circuit neural network and improved learning algorithm.Computer Engineering and Applications,2014,50（6）：213-218.

侯旋（1979—），男，博士，研究方向：智能信息处理、量子信息处理。

2012-05-24

2012-07-30

1002-8331（2014）06-0213-06

CNKI网络优先出版：2012-08-20，http://www.cnki.net/kcms/detail/11.2127.TP.20120820.1518.002.html