双参数五点插值细分法
2014-07-07张艳艳檀结庆
张艳艳,檀结庆
合肥工业大学数学学院,合肥 230009
双参数五点插值细分法
张艳艳,檀结庆
合肥工业大学数学学院,合肥 230009
提出包含两个参数的五点ternary插值细分法。利用生成多项式等方法对细分法的一致收敛性,CK连续性进行了分析。讨论了参数对细分法的收敛性及连续性的影响,同时给出了细分法C0到C2连续的充分条件和数值算例。
ternary细分法;插值;一致收敛性;CK连续性
1 引言
细分方法是一种根据初始数据或初始控制多边形由计算机直接生成曲线曲面或其他几何形体的离散化的造型方法。具有算法简单、易于实现和高效性等优点,因而在几何造型中得到广泛应用。1987年Dyn等[1]提出生成曲线的四点插值细分法(C1连续)。Dyn等[2-3]从理论上对binary细分法及其极限曲线的存在性及光滑性进行了研究。Hassan等[4-5]提出ternary四点插值细分法,生成的极限曲线达到C2连续,并给出了三重格式的一些充分条件。郑红婵等[6-8]将四点插值细分法进行推广,提出了一类包含两个形状参数的双参数四点binary细分法和多参数ternary细分格式。蔡志杰[9-10]对非均匀控制顶点时四点法及变参数四点法的收敛性和连续性进行了分析。丁友东[11]提出非线性四点插值细分法。Faheem等[12]提出了ternary六点插值细分法,生成曲线达到C2连续。
提出了双参数五点ternary插值细分法,利用生成多项式等方法对细分法的收敛性和连续性进行了分析。可以通过调节形状参数取值来实现对细分曲线形状的调控,并达到一致收敛,C1或C2连续。
2 预备知识

其中∂={∂j|j∈Z}⊂R,其中J0为有限下标集,∂j中只有有限个数不为零,称为该细分法的mask,将此细分法表示为S,因此有Pk+1=SPk,S为线性算子,表示从Pk到Pk+1的线性变换。一般地,有Pk+1=SPk=Sk+1P0。
定义1对于ternary细分法S和初始控制点集f0=为第k次细分后的控制点集,且对应的参数为(h为初始值的步长),若存在定义在R或R子集上的不恒为零的连续函数f(x),满足则称细分法S一致收敛,记S∈C0,并记f(x)=S∞f0。若S∞f0∈CK,则称细分法S为CK连续的,简记为S∈CK。
定理1[4,8]若由式(1)定义的ternary细分法S一致收敛,则其mask∂={∂j}满足:
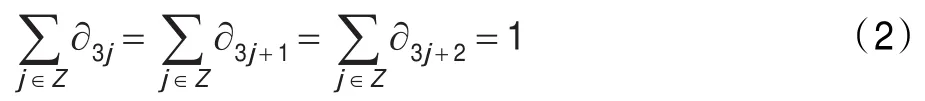
定理2[4,7]设ternary细分法S的mask∂={∂j}满足式(2),则存在一个细分法S1,满足:dfk+1=S1dfk。fk= Skf0且记Sn的mask为∂(n)={∂},其生成多项式为:

定理3[4,8]ternary细分法S一致收敛当且仅当细分法S1对任何初始数据f0一致收敛于零,即
定理4[4,8]设ternary细分法S一致收敛,则S决定了一个紧支集上唯一的连续函数S∞f0。

3 双参数五点ternary插值细分法

其中ω,μ为形状参数。
上述规则可改写为:
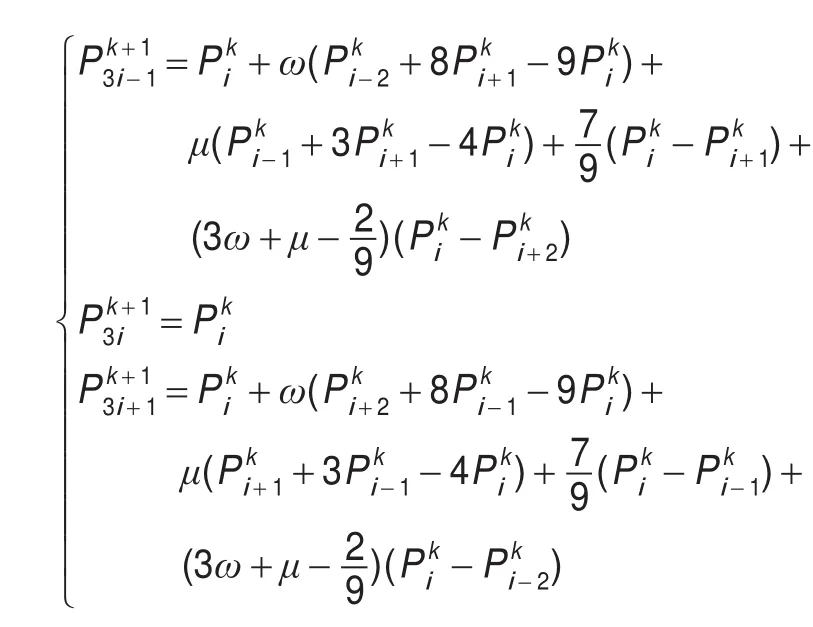
ω,μ的几何意义如图1所示。

图1 参数μ,ω的几何意义

4 双参数五点ternary插值细分的收敛性和连续性分析

定理6当参数μ,ω满足:

时,此细分法一致收敛,即存在惟一紧支集的连续函数S∞P0∈C0[0,n]为其极限函数。


时,此细分法是C2连续的。形状参数取值域如图2所示。
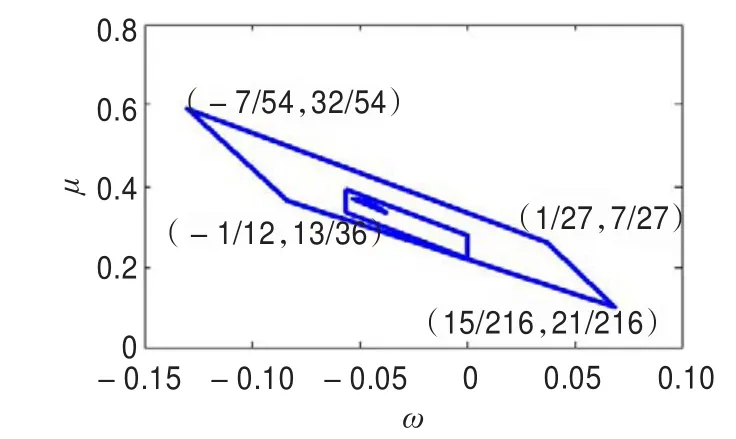
图2 双参数五点插值法的参数取值域
5 结论与数值算例
在Hassan四点插值细分法的基础上提出了双参数五点ternary插值细分法。算法中引入了两个控制参数,增强了对极限曲线的可控性。且由于五点法相对于四点法增加了控制顶点,产生的曲线整体上与控制点的关系更加密切。图3-1所示为采用本文方法,经过5次细分所得到的C1~C2连续的细分曲线图形(虚线为初始控制多边形,实线为利用本文方法生成的极限曲线)。

图3 -1双参数五点插值法C1和C2细分曲线
图3-2(a)是文献[4]方法经过10次细分后生成的极限曲线,图3-2(b)是本文方法经过5次细分后生成的极限曲线。比较可知,本文方法经过较少的细分次数可以得到与文献[4]方法相同效果的极限曲线。

图3 -2文献[4]方法细分曲线和本文方法细分曲线
图4以固定μ值(μ取0.35)为例说明了形状参数ω的取值对细分曲线形状的影响。可以看出,固定形状参数μ另一形状参数ω在一定范围内从小到大逐渐增加时,极限曲线先“向外插值”,再“向内插值”,同时向内微缩。图5以ω取定-0.045为例说明形状参数μ的取值对细分曲线也有类似影响。

图4 参数ω对细分曲线形状的影响
如果选取某些特殊的参数值会使极限曲线产生如图6所示的分形现象。

图5 参数μ对细分曲线形状的影响
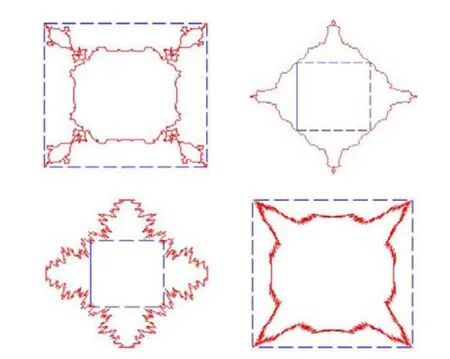
图6 分形现象
实验表明,多点数的三重细分法具有分形性质,但除经典的细分法外(文献[13-15]给出证明),并没有完整的关于多点数细分法的分形性质的理论证明。这方面有待于进一步研究。
[1]Dyn N,Levin D,Gregory J A.A 4-point interpolatory subdivision scheme for curve design[J].Computer Aided Geometric Design,1987,4(4):257-268.
[2]Dyn N,Gregory J A,Levin D.Analysis of uniform binary subdivision schemes for curve design[J].Constructive Approximation,1991,7(2):127-147.
[3]Dyn N.Subdivision schemes in computer-aided geometric design[C]//Lighted W.Advances in Numerical Analysis.[S.l.]:Clarendon Press,1992:36-104.
[4]Hassan M F,Ivrissimitzis I P,Dodgson N A.An interpolating 4-pointC2ternary stationary subdivision scheme[J]. Computer Aided Geometric Design,2002,19(1):1-18.
[5]Hassan M F,Dodgson N A.Ternary and three-point univariate subdivision schemes[C]//Proceedings of Curve and Surface Fitting:Saint-Malo 2002.Brentwood:Nashboro Press,2003:199-208.
[6]郑红婵,叶正麟,赵红星.双参数四点细分法及其性质[J].计算机辅助设计与图形学学报,2004,16(8):1140-1145.
[7]郑红蝉,叶正麟,赵红星.双参数C2插值细分法[J].西北工业大学学报,2004,22(3):329-332.
[8]胡玫瑰,郑红婵,许婷,等.静态ternary逼近细分格式的连续性分析和构造[J].计算机工程与应用,2011,47(9):167-170.
[9]Cai Zhijie.Convergence,error estimation and some properties for four-point interpolation subdivision scheme[J]. Computer Aided Geometric Design,1995,12(5):459-468.
[10]Cai Zhijie.The theory and application of four-point scheme with non-stationary parameter[J].Chinese Annals of Mathematics:Ser A,1995,16(4):524-531.
[11]丁友东.一类非线性保凸插值离散细分格式及其性质[J].复旦学报,2000,39(1):9-14.
[12]Faheem K,Mustafa G.Ternary six-piont interpolating subdivision scheme[J].Lobachevskii Journal of Mathematics,2008,29(3):153-163.
[13]Zheng Hongchan,Ye Zhenglin,Chen Zuoping,et al.Fractal rang of a 3-point ternary interpolatory subdivision scheme with two parameters[J].Chaos,Solitons and Fractals,2007,32(5):1838-1845.
[14]Zheng Hongchan,Ye Zhenglin,Lei Youming,et al.Fractal properties of interpolatory subdivision schemes and their application in fractal generation[J].Chaos,Solitons& Fractals,2007,32(1):113-123.
[15]Wang Juan,Zheng Hongchan,Xu Feng,et al.Fractal properties of the generalized chaikin corner-cutting subdivision scheme[J].Computers&Mathematics with Applications,2011,61(8):2197-2200.
ZHANG Yanyan,TAN Jieqing
School of Mathematics,Hefei University of Technology,Hefei 230009,China
A new scheme is presented to design subdivision curves by introducing two control parameters in the ternary subdivision scheme.The sufficient conditions of the uniform convergence property andCKcontinuity properties of the five-point ternary subdivision scheme with two parameters are proved.It can generateC2limit functions by choosing two parameters appropriately.Some examples of the curve design are given to show the efficiency of the proposed subdivision scheme.
ternary subdivision scheme;interpolation;uniform convergence;CK-continuity
A
TP391.72
10.3778/j.issn.1002-8331.1211-0081
ZHANG Yanyan,TAN Jieqing.Five-point interpolating subdivision scheme with two parameters.Computer Engineering and Applications,2014,50(6):135-138.
国家自然科学基金(No.60773043,No.61070227);教育部科学技术研究重大项目(No.309017);国家自然科学基金-广东联合基金重点项目(No.U1135003)。
张艳艳(1989—),女,硕士研究生,主要研究方向:计算机辅助几何设计;檀结庆(1962—),男,教授,博导,主要研究方向:非线性数值逼近理论与方法、科学计算、计算机辅助几何设计、计算机图形学、图像处理技术。E-mail:hfutzhyy@sina.com
2012-11-06
2013-01-15
1002-8331(2014)06-0135-04
CNKI网络优先出版:2013-01-29,http://www.cnki.net/kcms/detail/11.2127.TP.20130129.1539.010.html
