彩色空间阈值分割的色差变换方法研究

唐从飞，韩潇，彭力

江南大学物联网工程学院，江苏无锡 214122

彩色空间阈值分割的色差变换方法研究

唐从飞，韩潇，彭力

江南大学物联网工程学院，江苏无锡 214122

为实现对图像更好的阈值分割，针对原始色差变换存在的同色异值、异色同值的问题，基于HSI彩色空间色差变换，提出正余弦交叉法（SCCM）取参考点。该变换方法是根据各点色调正余弦值计算总体正、余弦均值，再由此求得对应的色调值。方法能够根据不同图像自适应地计算色差变换的参考点，使得变换后的灰度图有较好的灰度分布，为阈值分割提供更好的分割对象，提高分割质量。

正余弦交叉法；HSI空间；色差变换；参考点

1 引言

阈值分割在图像处理、图像分析中有广泛的应用[1]，在医学图像分割、运动跟踪、三维重建等领域中受到广泛的重视[2]。在HSI空间中，使用彩色差是计算该空间中两点弧线距离的一种方法，由此产生的色差变换能够将HSI空间中的各点映射到灰度图像当中[3]。然而直接对图像进行变换存在同色异值、异色同值等问题[4]。

为解决直接色差变换上述问题，本文在此基础上提出正余弦交叉法计算色差变换所需要的参考点。

2 彩色空间转换

图像的表示方式有多种，其中彩色图像表示有RGB、HSI、LAB等模型[5-6]。

2.1 图像的HSI彩色空间

目前，大多数彩色图像采用RGB色彩空间，但本文采用HSI色彩空间，它是美国色彩学家M unseu于1915年提出的，它反映了人的视觉系统感知彩色的方式，同时也有利于图像处理[7]。它以色调、饱和度和强度三种基本特征量来感知颜色，在HSI色彩空间中，色调H （Hue）与光波的波长有关，它表示人的感官对不同颜色的感受，如红色、绿色、蓝色等，它也可表示一定范围的颜色，如暖色、冷色等[8-9]。饱和度S（Saturation）表示颜色的纯度，纯光谱色是完全饱和的，加入白光会稀释饱和度。饱和度越大，颜色看起来就会越鲜艳，反之亦然。强度I（Intensity）对应成像亮度和图像灰度，是颜色的明亮度[10]。

由RGB色彩空间到HSI色彩空间的转换由下式给出[11]：

其中，θ为：

物体的色度和饱和度通常由构成物体的原材料的光线吸收和反射特性来决定，而亮度明显地受光照和视角的影响[12]。一般的基于灰度的图像阈值分割容易受到光照不均匀以及阴影的干扰，引入彩色图像的色度的信息后可以降低这些干扰，使分割结果更接近真实情况[13]。

2.2 HSI空间色差变换

为将图像的彩色信息引入图像分割中，本文采用色差转换，将HSI空间的各点根据其彩色属性，变换为相应的灰度图像，即彩色差，该灰度图像包含了图像的彩色信息，在充分利用图像的彩色信息的同时，减少计算复杂程度。

假设HSI空间中的两个彩色属性值分别为V1= (H1，S1，I1)T和V2=(H2，S2，I2)T，彩色差定义为：

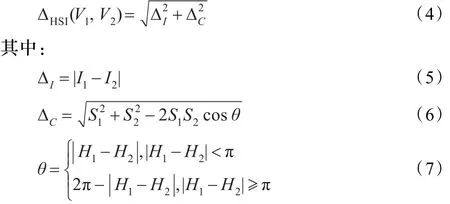
从公式可以看出，色差变换是两点在HSI柱形坐标中的距离，表示两点之间的差异性大小，可利用此特性将彩色图像转换为对于某点的灰度图。

3 选取色差变换参考点

彩色差一般用于区域间的分割交换，本文是为实现阈值分割将整幅图像中的各像素点转换为相对于某一参考点的空间彩色差图像，与本文的使用环境有所区别，要选择相应的参考点来配合色差变换。

3.1 特殊点作为参考点

HSI空间中H用角度表示，取值范围为[0，2π），S和I的取值范围均为[0，1]。则坐标的特殊点可以有O（0，0，0），B（0，1，0），C（0，0，1），D（0，1，1）。

由公式（6）中的项2S1S2cosθ可以看出色调H的信息是通过饱和度值表现出来的。当式中有一个S取零时，色调的余弦值的系数为零，不能够被表现在彩色差变换的结果当中。由于O、C两点饱和度都为0，故不选作参考点。

B、D两点分别位于圆柱坐标的上、下边缘处，相对于HSI空间中所有点的整体变换效果相同。B、D两点的选取不同对结果无明显影响，故选B点为色差变换的参考点，对图2作色差变换分析。

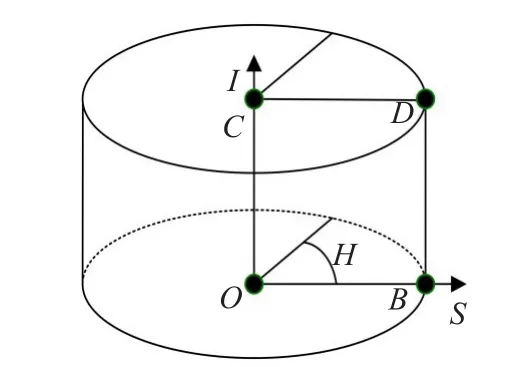
图1 HSI坐标及其中的特殊点

图2 满饱和测试图

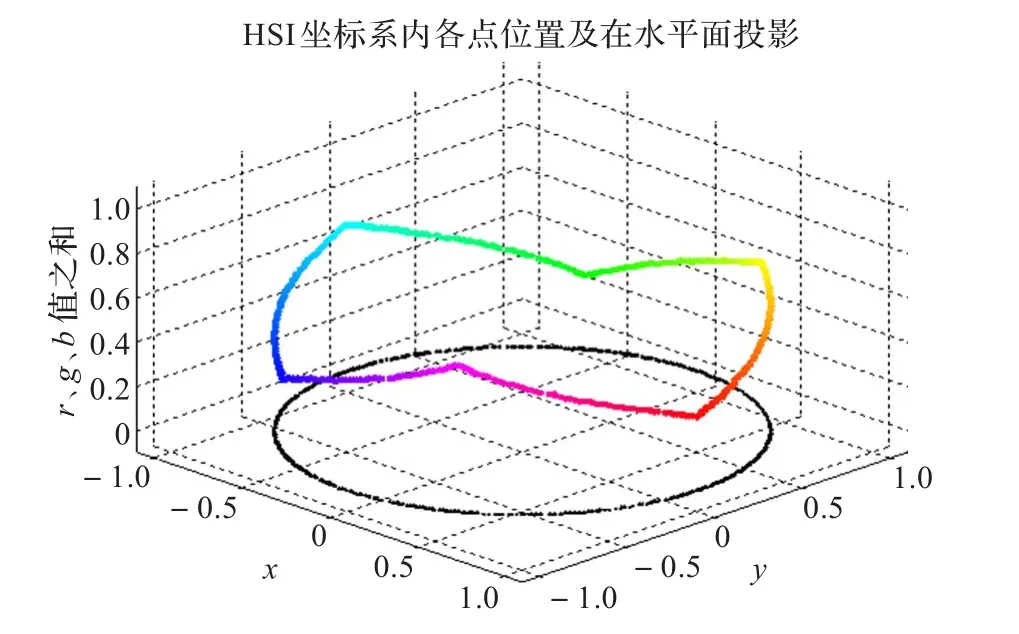
图3 各点投影

如图4（c），原图色调值域[0°，360°）的左、右边界处颜色表现相近却有色调值突变的问题。色差变换在不破坏HSI彩色空间模型可以降低光照影响的性能的同时，解决了红色区域对应的色调值存在突变的问题。

由图4（f）可以看出色差变换后的图像于180°处呈轴对称图形，从中间的湖蓝向两边绿、蓝色的数值变化趋势一致，在绿、蓝色处有相同的色差变换值，这从图5的分析中也可以看出，2π/3与4π/3处值相等。

图4 各值对应灰度图及变换结果

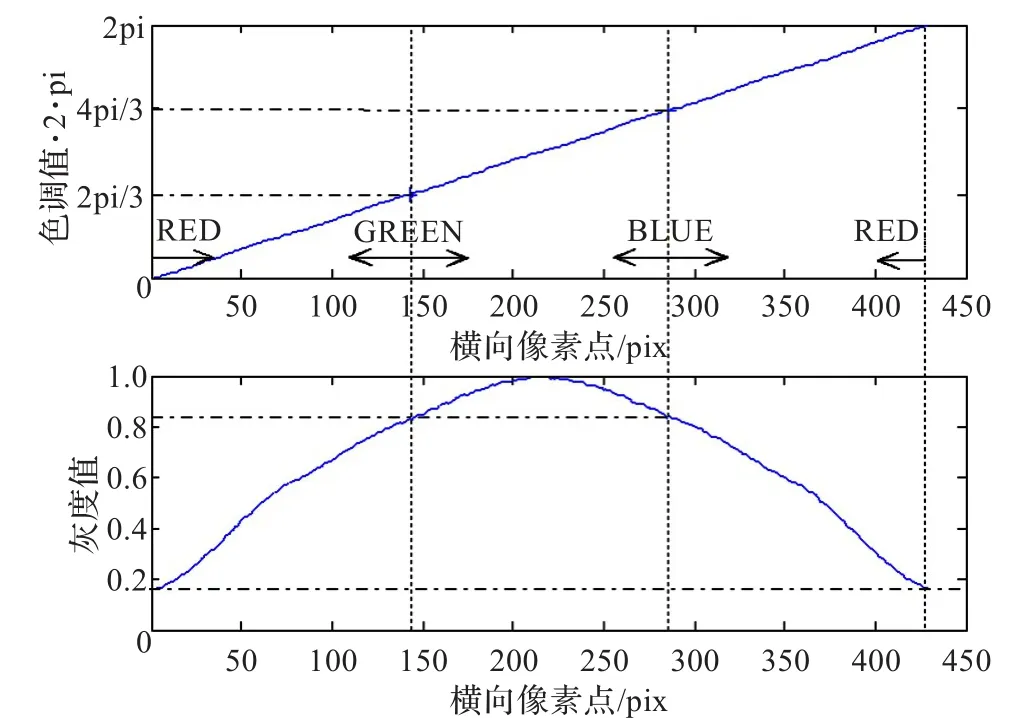
图5 色调值及变换曲线

当选取图1中点B（0，1，0）为参考点时，彩色差模型在定义域（0，2π）上的值域是以π为轴对称的。此时彩色差模型不能够有效地区别色调在定义域（0，π）与（π，2π）上的颜色差别，也就是在进行色差变换时不同的颜色会出现相同的彩色差值。

3.2 图像色调均值作为参考点色调

色差变换时的参考点的选取应该根据图像的具体情况来确定。自然图像中出现如图2，像素点颜色均匀分布，色度都是100%，亮度有规律的分布的情况是极少的。通过选取点B（0，1，0）为色差变换参考点的仿真实验中可以发现，在HSI圆柱形坐标中，参考点色调的确定尤为重要。当图像的色调分布在某一区域时，若取参考点的H值为图像色调的平均值，可做如下分析：

暂且撇开H空间区域左右极值处颜色相等问题，设图像色调均值为hˉ：

点M、N分别处于色调均值的左右邻域，点M∈ˉ-δ，，点N∈(ˉ+δ)，λM、λN∈(0，1)。分析知在通过公式（7）计算θ时H1-H2|=δ的值恒小于π。则：

若取λM=λN，则θM=θN，M、N两点的色调贡献值相同，而两点处的颜色是不同的。由此可以知道，当参考点的色调取为均值hˉ时，色调H轴上点hˉ两侧图像的色调分量对色差变换的影响相等，若图像色调分布呈多峰，该变换不能够有效区分色调差异，与变换的目的相违背。

由以上分析可知，对于一幅已知的图像，色差变换时，参考点的H值的选取应在图像色调集中区域的一端，才能使变换对不同的色调值产生不同的变换结果。在变换时使用到了式（6）-（7），余弦函数是以2π为周期的周期偶函数，则有：

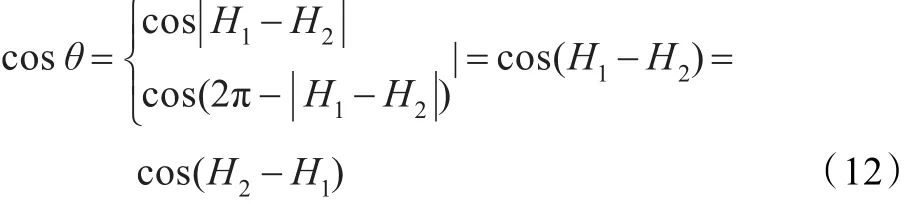
右侧与左侧取参考点色调值并无差异，习惯在该区域的左侧选取。

3.3 正余弦交叉法取参考点

正余弦交叉法（Sinusoidal Cosine Cross M ethod，SCCM）选取参考点色调关键在于图像色调中心点的确定，而色调中心点的确定又与每一幅图像色调密切相关。因为红色区域跨在色调定义域的两端，假设图像中的像素点的色调在圆柱坐标中0点处呈三角分布，则在H轴上是图6分布情形，取到的平均值会在π的位置处，与实际情况0或2π不符，之间相差π。故不能直接对色调取平均值。

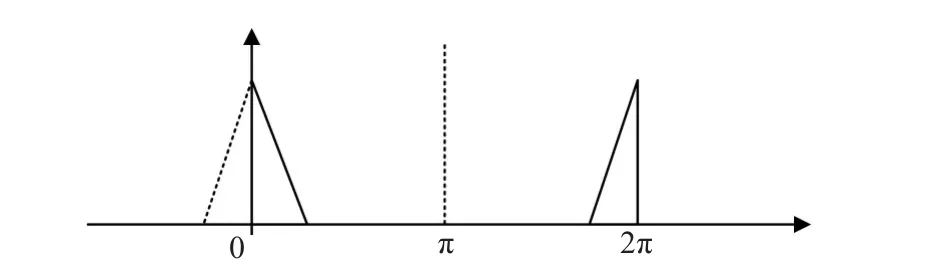
图6 色调特殊分布及均值

那么该如何来取图像色调中心值呢？

本文提出正、余弦结合的方法，联合求中心点P。

因正弦、余弦函数都是非单调函数，单独使用正弦逆函数或单独使用余弦逆函数求目标值都会得出双值，不能单独确定要求的色调中心值。现将两者结合，如图7示，步骤如下：

（1）将各像素点的色调值乘以2π，由区间[0，1）映射到[0，2π）。

（2）求各像素点对应的正弦、余弦值。

（3）分别对正弦值矩阵、余弦值矩阵求平均值m、n。

（4）根据所求得的正弦、余弦均值作L1、L2横竖两条直线分别割圆O于(P，P1)、(P，P2)。

（5）则两对交点的共同点P对应的值即为所要求的色调中心值。

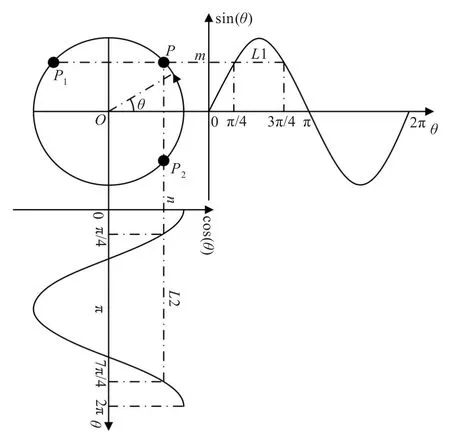
图7 正余弦联合求中心值几何原理图

根据所求得的色调中心值，选取向左偏移π/2即为色差变换的最终参考点色调值。对于参考点的另外两个参数饱和度与亮度不存在色调的复杂情况，可直接取为零。则最终的参考点为(HP，0，0)。

然而，图7所示的P点绝大多数情况是不在圆上的，即两条线与圆的两对交点很少会在圆上，基本上会出现在圆内部，如图8。

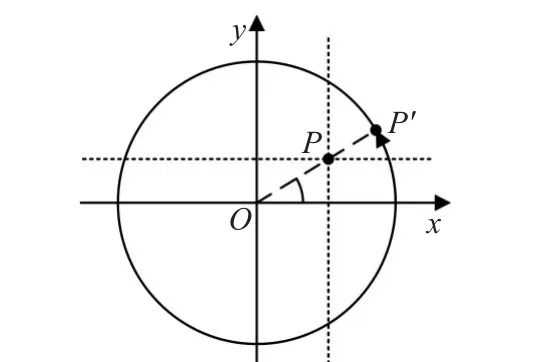
图8 通常情况下P的位置

此时，要求的色调区域中心值就P点所对应P′的角度确定。

P′与交点的关系可由式表示：

4 小波分解提取阈值

f(x)是一个离散序列，则对f(x)展开得到的系数称为f(x)的离散小波变换（DWT）。

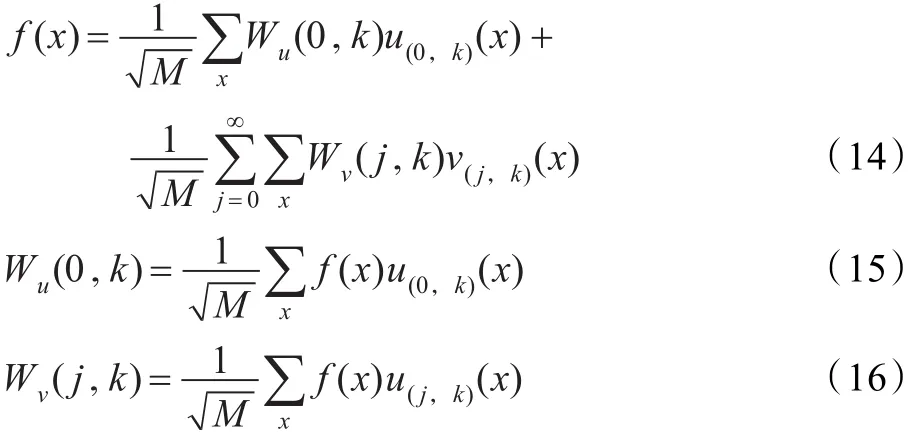
一般选M为2的整数次幂，所以上述求和时对x=0，1，…，M-1，j=0，1，…，J-1，k=0，1，…，2j-1进行。系数Wu(0，k)和Wv(j，k)分别为近似系数和细节系数[14-15]。

利用小波函数的特性，可以对彩色差图像作多分辨率的分析，尺度参数M决定分解的尺度，小尺度分析细节特性，大尺度分析总体特性。选取小波系中具有对称性的db1(N=1)小波（与haar小波相同）为小波变换函数，对彩色差图像直方图进行小波变换。

适当尺度下小波分解出来的低频波谷点就是可能的阈值分割的分割点。

对某两幅图像的彩色差图像直方图作小波分解，选取合适的小波参数，如图9。随着分解层数的增加，波谷数量减少，根据不同图像的彩色差图像直方图分解结果可以看出，当分解层数level=3时，能够得到较准确的分割阈值。故下文阈值分割仿真所选取的小波分解参数为：db1(N=1)，level=3。

图9 不同图像不同分解层数的低频系数

5 实验结果与分析

5.1 归一化测度

归一化测度是评价图像分割质量的一个衡量指标，其函数表达形式为：

其中ωi是每一类的概率，是每一类的方差，是图像的总方差。U的取值范围是[0，1]，U越大表示分割质量越高。

5.2 算法仿真

为验证本文算法的有效性与优越性，现用M atlab仿真平台，设计仿真程序，处理步骤如图10所示。

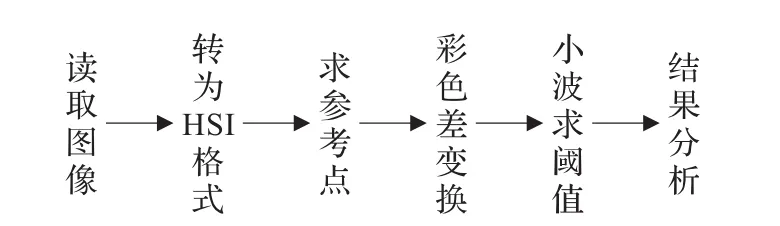
图10 算法处理步骤

图11为四幅彩色图片在使用SCCM法和原始方法处理效果对比。图（c1）中人物脸部、肩部、饰品以及背景各部分差异较小，相互之间差异较明显，效果优于（b1）；（c2）（c3）效果优于（b2）（b3），（b2）中红色椒和（b3）中的天空存在明显的突变，而（c2）（c3）中没有出现此问题；（c4）中不同颜色的物体对应不同的灰度，而（b4）中蓝色桌面与绿色的桔子却表现出相近的灰度。（d1～d4）为各图采用本文所提方法分割后的图像。

5.3 数据分析

在使用相同的分割方法下，对比使用两种色差变换方法对分割的结果和性能的影响。可以看出，本文所提的SCCM色差变换算法在分割质量评价指标归一化测度U上有明显的优势。本文所提的方法在时间上要略高于原始方法，但综合性能要好，在耗时相当的情况下能够有更好的分割效果，提高图像分割质量。

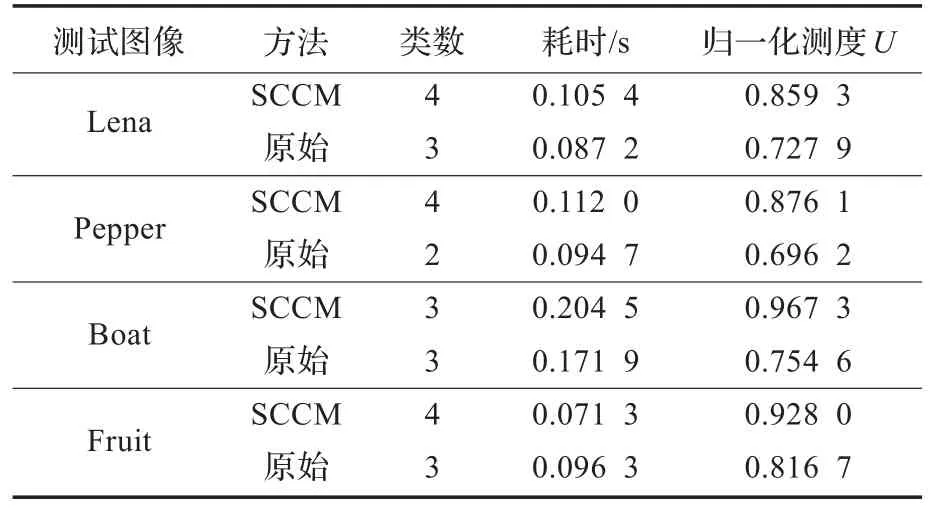
表1 两种变换方法分割结果比较

6 结束语

本文提出基于HSI彩色空间彩色差的算法改进，解决了基础色差变换存在的同色异值、异色同值等问题。本文所提的SCCM变换方法能够根据不同图像自适应地选择色差变换的参考点，使得变换后的灰度图有较好的灰度分布，为后续阈值分割算法提供更好的分割对象。仿真结果表明，在使用相同分割算法时，SCCM变换方法效果明显优于原始色差变换，可应用于实际图像处理和工程当中。

图11 处理效果对比

[1]Huang Deng-yuan，Wang C H.Optimal multi-level thresholding using a tw o-stage Otsu optimization approach[J]. Pattern Recognition Letters，2009，30（3）：275-284.

[2]Osher S，Sethian J A.Fronts propa-gating with curvaturedependent speed：algorithms based on Ham ilton-Jacobi formulateons[J].Journal of Computational Physics，1988，79（1）：12-49.

[3]Fan Jiulun，Zhang Xuefeng，Zhao Feng.Three-dimension maximum between-cluster variance image segmentation method based on chaotic optimization[C]//Lecture Notes in Computer Science 4222.[S.l.]：Springer，2006：164-173.

[4]李厚强，刘政凯，詹曙.一种彩色纹理图像的分割方法[J].计算机学报，2001，24（9）：965-971.

[5]倪培梅.光照变化下颜色模型稳定性比较[J].计算机光盘软件与应用，2012，1（7）.

[6]严春来.彩色图像分割算法的研究[D].成都：电子科技大学计算机科学与工程学院，2008：10-11.

[7]原春锋，王传旭，张祥光，等.光照突变环境下基于高斯混合模型和梯度信息的视频分割[J].中国图象图形学报，2007，12（11）：2068-2072.

[8]杨克己，邵泉钢.基于多分辨率阈值的非均匀光照微视觉图像实时分割技术研究[J].工程设计学报，2011，18（2）：139-144.

[9]高业文，熊鹰，潘晶晶，等.基于IGA与GMM的图像多阈值分割方法[J].计算机应用研究，2012，29（3）：1130-1134.

[10]吴一全，朱兆达.图像处理中阈值选取方30年（1962-1992）的进展（一）[J].数据采集与处理，1993（3）：193-201.

[11]景晓军，李剑峰，刘郁林.一种基于三维最大类间方差的图像分割算法[J].电子学报，2003，31（9）：1281-1285.

[12]田军委，黄永宣.基于熵约束的快速FCM聚类多阈值分割算法[J].模式识别和人工智能，2008，21（2）：221-226.

[13]王永波，陈继荣.二维Otsu阈值分割算法的改进及应用[J].计算机仿真，2008，25（4）：263-264.

[14]杨福生.小波变换的工程分析与应用[M].北京：科学出版社，1999：112-121.

[15]宗常进，毕军涛，董军宇.基于离散小波变换的信号分解算法研究[J].计算机工程与应用，2009，45（8）：165-167.

TANG Congfei,HAN Xiao,PENG Li

School of IoT Engineering,Jiangnan University,Wuxi,Jiangsu 214122,China

In HSI color space,there’re some problem s with original color difference transformation such as the same color may be different values or different color with the same value.For solving the problem and achieving better effect of image threshold segmentation,the Sine&Cosine Cross Method（SCCM）is proposed to calculate the reference point based on original color difference transformation.This method can calculate the reference point of the transformation adaptively according to different image,which makes the grayscale image a better grayscale distribution,provides better segmented object,improves segmentation effect.

Sine&Cosine Cross Method（SCCM）;HSI color space;color difference transform;reference point

A

TP391

10.3778/j.issn.1002-8331.1209-0350

TANG Congfei,HAN Xiao,PENG Li.Research of color difference transformation method used in color space threshold segmentation.Computer Engineering and Applications,2014,50（16）：183-187.

国家自然科学基金（No.60973095）。

唐从飞（1988—），男，硕士研究生，主要研究领域为计算机图像处理、视觉跟踪；韩潇（1989—），男，硕士研究生，主要研究领域为图像处理；彭力（1967—），男，教授，博导，研究方向为视觉传感器网络、人工智能、计算机仿真。E-mail：tangfei719@163.com

2012-09-28

2012-11-08

1002-8331（2014）16-0183-05

CNKI网络优先出版：2012-12-19,http://www.cnki.net/kcms/detail/11.2127.TP.20121219.0957.001.htm l