混沌蚂蚁群优化求解自由节点B样条曲线拟合

徐善健，郭有强，戚晓明，夏伟

蚌埠学院计算机科学与技术系，安徽蚌埠 233000

混沌蚂蚁群优化求解自由节点B样条曲线拟合

徐善健，郭有强，戚晓明，夏伟

蚌埠学院计算机科学与技术系，安徽蚌埠 233000

B样条曲线拟合问题中，将节点作为自由变量可大幅提高拟合精度，但这就使曲线拟合问题转化为求解困难的连续多峰值、多变量非线性优化问题，当待拟合的曲线是不连续、有尖点情况，就更为困难。针对这一问题，基于混沌蚂蚁群优化算法CASO，提出了一种新的B样条曲线拟合算法CASO-DF。该算法结合B样条曲线拟合原理，通过蚁群中蚂蚁个体的混沌行为，调整自由节点位置，通过蚁群的自组织行为自适应地调整内部节点数目，解决了B样条曲线拟合问题。仿真结果表明了CASO-DF算法能够有效实现自由节点B样条曲线拟合，且性能优于其他同类算法。

曲线拟合；混沌蚂蚁群优化算法；节点放置；B样条

1 引言

在测试数据处理、逆向工程和图像处理等工程领域中，B样条曲线拟合技术应用较为广泛[1-2]。B样条曲线拟合问题是指：给定一组有序数据点，寻找一条B样条曲线通过或逼近这些数据点。B样条具有较好的逼近能力和强大的数学性质（局部修改，投影不变性等），可以非常灵活地表示种类繁多的形状。合适地产生B样条参数是获最优近似解的前提条件，特别是节点数目和位置选择对数据拟合精度有很大影响。

B样条曲线拟合问题已经引起众多学者关注，国内外的研究都取得了一定的进展。国内学者周明华、汪国昭[3]提出了基于遗传算法的B样条曲线，并解决了Bézier曲线拟合，表现较好的性能。郭改文、黄卡玛[4]提出一种模拟自然树生长的竞争优化算法，并将其应用在曲线拟合中。通过与遗传算法和经典最小二乘法对比两条经典的函数曲线拟合的结果，显示其算法的有效性。国外一些学者，采用固定节点数[5-7]，将B样条最小二乘拟合转化为简单的线性优化，拟合精度较低。Satoshi M等[8]提出一种新思想，采用自由节点（Free knot）代替固定节点，样条曲线的平滑程度由节点位置和节点的多样性来灵活调整。这种灵活性能抓住待拟合曲线的结构变化和适应分段曲线。因此，自由节点样条对非平滑数据拟合时，可以大幅度提高样条函数逼近程度，减少拟合误差。处理方法是：采用一定数量的自由节点，在迭代中修改自由节点数量，使之满足预定的误差界限[9]。该方法通常需要主观决策参数[10-11]（如误差容忍、平滑因子、代价函数和节点的初始位置），不能自动产生较好的节点向量，很难得到平滑的曲线。Lindstrom[12]进一步提出了克服主观决策的弱点，但其方法不适用于不连续、有尖点的拟合曲线。另一方面，从自由节点位置出发，Li 等[13]提出一个自适应节点放置（knot placement）方法，能够有效地自动选择合适的节点位置，但其仅适用于可微函数，并且很大程度上依赖于特征点（如曲率极值点和拐点）的信息，但有时很难获得这些信息。一个非常有希望的研究路线是基于元启发式算法放置节点。Yoshimoto等[14]将连续非线性、多变量优化问题转化为离散的组合优化问题，通过遗传算法解决。Ülker等[15]采用人工免疫算法代替遗传算法，得到较好结果。Zhao 等[16]采用随机优化方法逼近，通过高斯混合分布和聚类技术分布式评估获得节点，但该算法局限于封闭曲线。

综上所述，将B样条的节点作为自由变量，数据拟合精度会大幅度提高[17]，但是亟需克服以下困难：（1）采用自由节点时，B样条不是线性，而是线性与非线性参数的混合，形成较难的非线性最小二乘优化问题；（2）采用自由节点受最优节点位置解析式难以表达和最小二乘目标函数存在多局部最优等问题困扰；（3）采用自由节点向量包含节点数量和位置选取，若选取不当，可能导致绘制曲线不光滑，特别是不连续、带尖点的曲线。

为此，本文提出CASO-DF（Chaotic Ant Swarm Optimization for Data Fitting）算法，自适应地解决自由节点数量和位置选取问题。CASO-DF算法借助混沌蚂蚁群优化算法CASO[18]的非线性搜索能力，根据给定的数据特点自动产生多个自由节点、克服不连续和尖点带来的困难。实验结果表明提出的CASO-DF非常有效，不仅可以计算出最佳内部节点（Internal knot）数，而且可以得到最佳内部节点数目的最优拟合。

2 B样条数据拟合

k次B样条曲线B(t)可表示为[5-6]：

式中pi为控制点（Control point），i=1，2，…，n；Ni，k(t)为k次B样条在节点向量u={u0，u1，…，un+k}上的基函数，节点向量是区间[a，b]上的非减实数值节点。节点向量u的第一个和最后一个节点的重复度为k：u0=…=uk-1=a，un+1=…=un+k=b。不失一般性，假设[a，b]=[0，1]。Ni，k(t)是Cox-de Boor的递归函数[15]：

式中k=1，i=0，1，…，n+k-1。

式中k＞1，i=0，1，…，n。式（3）中，节点存在分子、分母，表明B(t)是节点的非线性函数。

不失一般性，假设待拟合的数据可以写成：

其中F(t)为数据的未知函数；εj为测量误差。式（4）运用最小二乘法，通过残差的平方之和Q决定B样条曲线B(t)的控制节点pj(j=0，1，…，n)：

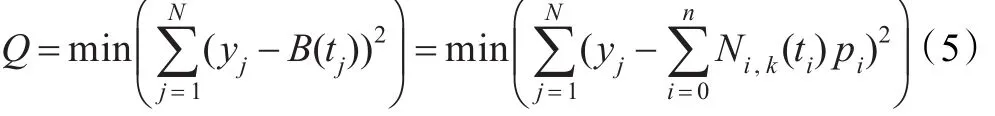
显然，目标函数Q依赖于B样条基函数和控制点。这样，求Q的过程就是解决连续的多峰值非线性最小化问题。

根据上述解释，目标函数式（5）和它的变量是B样条系数和内部节点。B样条系数是线性参数，而内部节点是非线性参数。显然这个最小化问题是一多峰值的最优化问题。

3 混沌蚂蚁群优化算法

混沌蚂蚁群优化算法（Chaotic Ant Swarm Optimization，CASO）基本原理源于蚂蚁个体的确定性混沌行为和蚁群的周期性自组织行为。CASO算法受蚂蚁混沌行为启发，基于动力学和最优值理论而设计。CASO是一种全局搜索算法，在求解函数优化[19]、参数识别[20]、聚类[21]等问题表现出较好的性能。CASO算法搜索范围与问题的搜索空间一致。设蚁群由M只蚂蚁组成，搜索空间RD是D-维实数连续空间。在蚂蚁的搜索空间S中，求函数f:S→R的最小值。因此，空间S中的每个点都是一个合法解。蚂蚁m的位置表示一个变量zm=(zm1，zm2，…，zmD)，m=1，2，…，M。CASO算法数学模型为[18]：

式中τ为当前迭代，(τ-1)为上一次迭代；ym(τ)为蚂蚁m当前迭代的组织变量，其初始值通常为ym(0)=0.999；rm为蚂蚁m的组织因子，它影响CASO的收敛速度。因为需要蚂蚁个体随时间演化有小的差异，所以选择rm值范围为0≤rm≤0.5，如rm=0.01+0.2×rand(1)；zmd(τ)是蚂蚁m第d维，d=1，2，…，D；qmd(τ-1)为蚂蚁m及其邻居在(τ-1)次迭代内发现的最优位置；a为较大的正数，可取a=200；b为常数0≤b≤2/3。ψd决定了变量的第d维的搜索区间[0，ψd]。文献[18]完整地讨论了式（6）中的参数与优化效果的关系。

在CASO算法中，蚂蚁邻居被定义为：在搜索空间中某蚂蚁周围一定距离内的有限只蚂蚁。文献[18]以欧氏距离作为判定邻居的依据。在搜索空间中，两只蚂蚁的位置分别为(zm1，zm2，…，zmD)和(zl1，zl2，…，zlD)，那么，这两只蚂蚁之间的距离为：

其中，m≠l，m，l=1，2，…，M。

为便于理解CASO-DF算法，图1给出混沌蚂蚁群优化算法CASO算法的流程图。由图1可以看出，CASO算法步骤：

（1）设置蚁群规模为N、迭代次数τ、每只蚂蚁的组织因子ri和位置xi。

（2）计算每只蚂蚁的当前目标函数值f(xi)，即适应值。

（3）计算每只蚂蚁及其邻居的最优位置pi。

（4）采用式（6）更新每只蚂蚁的组织变量yi和位置xi。

（5）判断是否满足终止条件，若满足，则退出；否则，转到步骤（2）。

图1 CASO算法流程图

4 基于CASO的数据拟合算法

根据第2章式（4），待拟合数据的未知函数可以用B样条曲线逼近。由混沌蚂蚁群优化算法CASO的特点，它是一种群体协同求解算法，在算法求解过程中，混沌个体的探索能力和群体的自组织能力相互结合，可以逼近任意的非线性函数[20]。于是，采用全局混沌蚂蚁群优化算法自动搜索决定最好的内部节点（Internal knot）{uk，uk+1，…，un}。下面基于CASO，提出B样条数据拟合获得最优节点向量的方法。

4.1 方案描述

设内部节点数为L，L=[λN]，其中0≤λ＜0.5，λ称为内部节点率，N是待拟合的节点数，0表示没有内部节点，0.5表示内部节点数是N的一半。因此，L是可变参数，采用CASO进行数据拟合时，不同蚂蚁处理的内部节点数不一定相同，也就是说，L对不同的蚂蚁维数不同。于是，假设蚂蚁m的维数L，每一维表示一个内部节点的实数值。图2给出一个编码实例。

图2 蚂蚁编码表示

图2中，每只蚂蚁的初始维数在L内随机产生，在混沌演化过程中，蚂蚁的维数可以根据邻居蚂蚁的适应值，调整其维数。蚂蚁的一个“空位”表示此维不需要，即内部节点数少1。

蚂蚁每维数值zmd(τ)有其混沌行为产生，根据蚂蚁的自组织行为更新其编码信息。终止条件为固定迭代次数Iter，经过多步迭代，每只蚂蚁逐步收敛到最优值。

4.2 适应函数

采用三个不同的适应函数。第一个是残差之和Q，如式（5）所示，这种计算方法比较简单：仅需计算误差，不考虑计算模型的复杂度。因此，获得最好的误差需要牺牲大量的变量。考虑这个问题，采用其他两个适应函数，A IC（Akaike Information Criterion）[22]和BIC （Bayesian Information Criterion）[23]。这两个是惩罚信息论标准，通过简单地平衡精度，发现最优逼近模型，它们包括两项，第一项是模型函数的精度，第二项是最小化式中的自由参数数目的惩罚。AIC和BIC的表达式如下：

其中N是待拟合数据点数；Q由式（5）计算得到。由式（8）（9）可得，两个表达式很相似，但BIC较AIC应用了大量的惩罚。然而，不同点是对不连续、有尖点的函数，AIC可能产生不必要的冗余节点，因此，BIC更适用于自由节点数据拟合问题。

AIC和BIC的优势在于它们不需要主观参数，如误差边界、平滑因子。同时它们提供了一个简单和直观的过程决定最好的模型，AIC和BIC的值越小，适应值越好。于是可用它们选择最好的计算结果。

4.3 CASO-DF算法

由4.1节和4.2节，可得CASO-DF算法的伪代码。

算法1 CASO-DF算法的伪代码

输入：B样条次数k和待拟合的有序数据序列

5 实验结果及分析

5.1 仿真环境

为清楚展现CASO-DF算法的性能，采用文献[14]中的3个函数作为本文的测试函数，如表1。表1给出了函数的表达式和定义域。图3给出了三个函数的图像，显示三个测试函数的特性。选择这些函数的原因：首先，检验算法适用多样性；其次，其他B样条数据拟合算法常采用这些函数。函数包括连续平滑、不连续、有尖点三种类型。每个函数采样201个数据点，n-k为内部节点数。这些点按照正弦函数g(t)=e2tsin(20t)的均匀随机采样U(0，1)。同时为了检验提出方法的鲁棒性，对数据增加白噪音ξ，ξ符合正态分布N(0，σ2)，平均值为0，方差为σ2，三个函数的标准差为σ=0.1。

f1(t)是一个除t=0.4之外都是连续光滑的，在t=0.4时，函数发生阶跃的函数。f2(t)是一个富有挑战性的函数，在t=0.6处非连续，且此点两侧函数增减性不同。f3(t)在t=0.5时有尖点，是一种比较好的、适用于评价CASO-DF的函数。

仿真实验的硬件环境是CPU Intel Core 2 Duo 2.4 GHz，内存2 GB，软件环境是W indow s XP，以M atlab 7.0作为实验工具。CASO-DF算法最大进化代数为200，蚁群规模为20。其他相关参数按式的要求设置。

5.2 仿真结果及分析

表1 测试函数

为验证CAS-DF算法的性能，对f1(t)、f2(t)、f3(t)适应值与内部节点数之间的关系以及它们随迭代次数增加的演化收敛趋势进行仿真和分析。在仿真图中，‘x’点是根据仿真函数加入白噪音ξ后生成。

图4的（a）（b）（c）分别给出了f1(t)的AIC、BIC适应值变化与内部节点数之间的变化趋势，BIC适应值和内部节点数随迭代次数的演化情况以及f1(t)的4阶B样条曲线拟合的最好仿真结果。

图5的（a）（b）（c）分别给出了f2(t)的AIC、BIC适应值与内部节点数之间的演化趋势，BIC适应值和节点数随迭代次数的变化情况以及f2(t)的4阶B样条曲线拟合的最好仿真结果。

图6的（a）（b）（c）分别给出了f3(t)的AIC、BIC适应值与内部节点数之间的演化趋势，BIC适应值和节点数随迭代次数的变化情况以及f3(t)的4阶B样条曲线拟合的最好仿真结果。

由图4～6中可以看出，CASO-DF算法都能产生较好的B样条曲线。图4～6中的（a）显示当内部节点数量少时，AIC和BIC相对较大。AIC和BIC随内部节点数增加而减小，直至达到最小值，之后它随内部节点数增加而增大，表明了f1(t)、f2(t)、f3(t)三个函数的最优内部节点数分别为4、8、5。图4～6中的（b）表明了BIC和内部节点数随迭代次数演化的收敛性。以三个函数的最优内部节点数，分别绘出图4～6中的（c）4阶B样条拟合曲线。

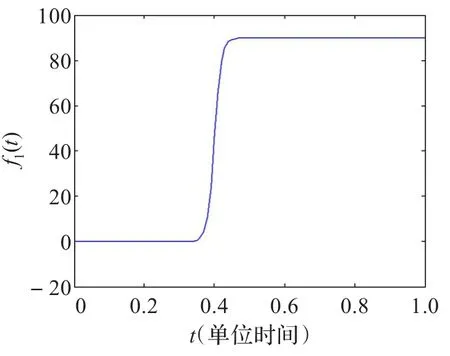
图3 （a）f1(t)的函数图像

图3 （b）f2(t)的函数图像

图3 （c）f3(t)的函数图像

具体看，图4（c）f1(t)的结果与文献[14]一致，表明CASO-DF算法拟合效果较好。图5（a）表明f2(t)的适应值AIC、BIC有相同的特征，都随内部节点数从1到7增加而急剧减少，内部节点数为8时有最小值。随内部节点数增加，适应值AIC、BIC缓慢增大。图6（a）中，内部节点数从1到4，f3(t)的适应值AIC、BIC急剧下降，最好的内部节点数为5。随内部节点数增加，适应值AIC、BIC缓慢增大。图4～6（c）表明了CASO-DF算法能够对连续、非连续、有尖点函数进行数据拟合。为体现图4～6（c）中CASO-DF算法自动放置能力，表2给出三个函数的内部节点数目及放置的横坐标。

由图4（c）、图5（c）、图6（c）和表2可以看出，CASO-DF算法不仅能够获得三种函数的较好的数据拟合结果，而且能够得到最优内部节点的位置，其原因在于CASO-DF算法的混沌行为可以搜索到内部节点的位置，而自组织行为可使蚁群选取到最少内部节点数目。

图4 （a）函数f1(t)的AIC、BIC适应值与内部节点数之间的关系

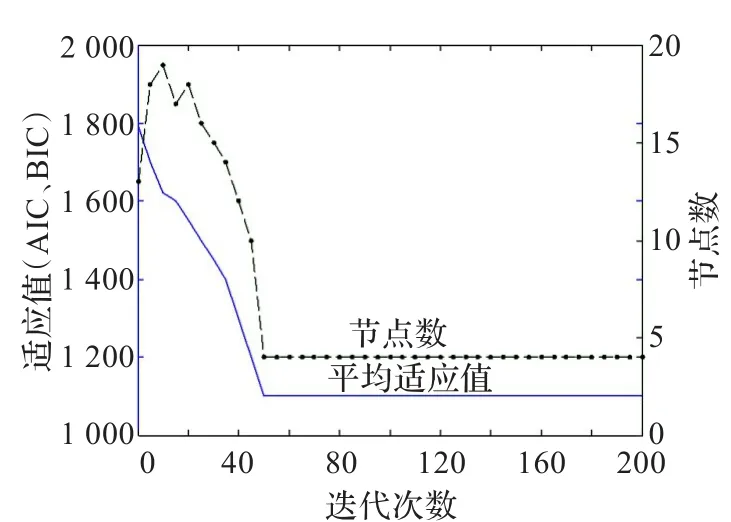
图4 （b）函数f1(t)的BIC适应值和内部节点数随迭代次数演化过程

图4 （c）函数f1(t)的4阶B样条曲线拟合结果

图5 （a）函数f2(t)的AIC、BIC适应值与内部节点数之间的关系

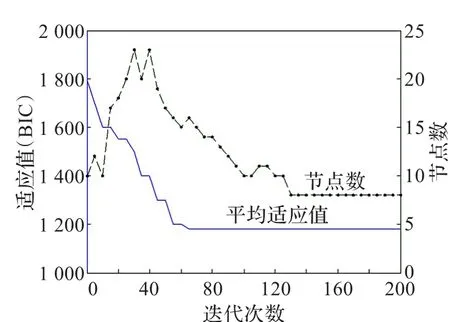
图5 （b）函数f2(t)的BIC适应值和内部节点数随迭代次数演化过程

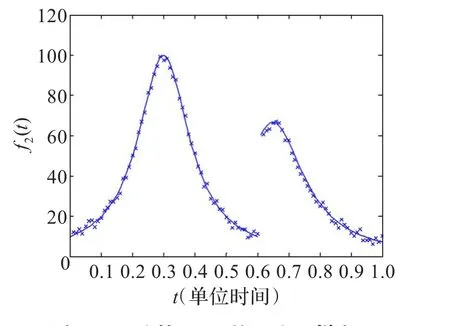
图5 （c）函数f2(t)的4阶B样条曲线拟合结果

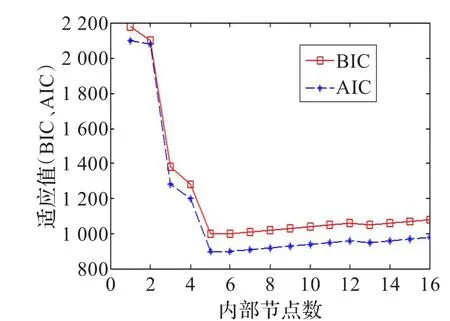
图6 （a）函数f3(t)的AIC、BIC适应值与内部节点数之间的关系

图6 （b）函数f3(t)的BIC适应值和内部节点数随迭代次数演化过程

图6 （c）函数f3(t)的4阶B样条曲线拟合结果

表2f1(x)、f2(x)、f3(x)最优内部节点数及位置

5.3 与其他算法的比较

为了评估所提出的CASO-DF算法的节点自动放置能力，将该算法与演化相关算法[14-16，24-25]进行比较。Yoshimoto等[14]将数据拟合作为基于遗传算法的离散组合优化问题。Ülker等[15]采用人工免疫算法处理数据拟合问题。Yoshimoto等[24]采用自适应实数编码的遗传算法。Sarfraz等[25]采用基于遗传算法和探测技术解决数据拟合问题。Zhao等[16]将高斯混合模型和k-均值方法结合，解决数据拟合问题。采用5.1节给出的测试函数，以M atlab7.0作为仿真工具，将CASO-DF算法与这些算法比较分析，相关算法的参数设置参考相关文献。表3考虑它们的迭代次数、计算时间等因素，给出了比较结果。“—”表示不存在。

表3 CASO-DF与相关算法的比较

从表3可以看出，CASO-DF算法较其他算法优秀，适用于多种类型的函数，特别是计算速度快。究其原因是，CASO算法是基于蚂蚁个体的混沌行为和整个蚁群的自组织行为设计，蚂蚁个体的混沌行为探索能力较强，对内部节点的位置搜索有较大帮助，而自组织行为能够较好协调个体之间的最优位置，加快了蚁群的搜索能力。因而CASO-DF算法的节点自动放置能力强于其他算法。

由5.2节和5.3节的仿真实验可以看出，基于CASO算法设计的CASO-DF算法，有较好的性能，在计算精度和计算时间上优于其他相关算法。

6 结束语

本文结合新型混沌蚂蚁群算法，提出了基于混沌蚂蚁群算法的B样条曲线拟合算法CASO-DF，该算法将节点作为自由变量，把B样条曲线拟合转化为连续多峰值非线性优化问题，应用CASO自动计算最优内部节点数，实现自由节点数目和位置自动选择。文中给出了混沌蚂蚁群算法解决曲线拟合问题的具体方法及步骤。仿真结果表明了CASO-DF在计算精度和计算速度方面优于相关算法。下一步的研究是将CASO-DF算法应用于图像边缘检测。

[1]PARK H.An error-bounded approximate method for representing planar curves in B-splines[J].Computer-Aided Geometric Design，2004，21（5）：479-497.

[2]Li W，Xua S，Zhao G.Adaptive knot placement in B-spline curve approximation[J].Computer-Aided Design，2005，37（8）：791-797.

[3]周明华，汪国昭.基于遗传算法的B样条曲线和Bézier曲线的最小二乘拟合[J].计算机研究与发展，2005，42（1）：134-143.

[4]郭改文，黄卡玛.模拟自然树生长的竞争算法及在曲线拟合中的应用[J].电子学报，2008，36（9）：1839-1842.

[5]Jing L，Sun L.Fitting B-spline curves by least squares support vector machines[C]//Proc of the 2nd Int Conf on Neural Networks&Brain.[S.l.]：IEEE Press，2005：905-909.

[6]Park H，Lee J H.B-spline curve fitting based on adaptive curve refinement using dominant points[J].Computer-Aided Design，2007，39：439-451.

[7]Wang W P，Pottmann H，Liu Y.Fitting B-spline curves to point clouds by curvature-based squared distance minimization[J].ACM Transactions on Graphics，2006，25（2）：214-238.

[8]Burchard H G.Splines（with optimal knots）are better[J]. Applicable Analysis，1974，3：309-319.

[9]Lyche T，Morken K.A data-reduction strategy for splines with applications to the approximation of functions and data[J].IMA Journal of Numerical Analysis，1988，8：185-208.

[10]A lhanaty M，Bercovier M.Curve and surface fitting and design by optimal control methods[J].Computer-Aided Design，2001，33：167-182.

[11]Goldenthal R，Bercovier M.Spline curve approximation and design by optimal control over the knots[J].Computing，2004，72：53-64.

[12]Lindstrom M J.Penalized estimation of free-knot splines[J]. Journal of Computational and Graphical Statistics，1999，8（2）：333-352.

[13]Li W，Xu S，Zhao G，et al.Adaptive knot placement in B-spline curve approximation[J].Computer-Aided Design，2005，37：791-797.

[14]Yoshimoto F，moriyama M，harada T.Automatic knot placement by a genetic algorithm for data fitting with a spline[C]//Proceedings of the International Conference on Shape Modeling and Applications.[S.l.]：IEEE Computer Society Press，1999：162-169.

[15]ÜLker E，Arslan A.Automatic knot adjustment using an artificial immune system for B-spline curve approximation[J].Information Sciences，2009，179：1483-1494.

[16]Zhao X，Zhang C，Yang B，et al.Adaptive knot placement using a GMM-based continuous optimization algorithm in B-spline curve approximation[J].Computer-Aided Design，2011，43：598-604.

[17]Molinari N，Durand J F，Sabatier R.Bounded optimal knots for regression splines[J].Computational Statistics&Data Analysis，2004，45（2）：159-178.

[18]Li L，Peng H，Wang X，et al.An optimization method inspired by chaotic ant behavior[J].International Journal of Bifurcation and Chaos，2006，16（8）：2351-2364.

[19]Ge F，Wei Z，Lu Y，et al.Disturbance chaotic ant swarm[J]. International Journal of Bifurcation and Chaos，2011，21 （9）：2597-2622.

[20]Peng H，Li L，Yang Y，et al.Parameter estimation of dynamical systems via chaotic ant swarm[J].Physical Review E，2010，81（1）.

[21]Wan M，Li L，Xiao J，et al.CAS based clustering algorithm for web users[J].Nonlinear Dynamics，2010，61：347-361.

[22]Akaike H.A new look at the statistical model identification[J].IEEE Transactions on Automatic Control，1974，19（6）：716-723.

[23]Schwarz G E.Estimating the dimension of a model[J]. Annals of Statistics，1978，6（2）：461-464.

[24]Yoshimoto F，Harada T，Yoshimoto Y.Data fitting with a spline using a real coded algorithm[J].Computer-Aided Design，2003，35：751-760.

[25]Sarfraz M，Raza S A.Capturing outline of fonts using genetic algorithms and splines[C]//Proc of Fifth International Conference on Information Visualization IV’2001.[S.l.]：IEEE Computer Society Press，2001：738-743.

XU Shanjian,GUO Youqiang,QI Xiaoming,XIA Wei

Department of Computer Science and Technology,Bengbu College,Bengbu,Anhui 233000,China

Data fitting through B-splines improves the accuracy of the solution dramatically if the knots are treated as free variables.However,in this case the problem becomes a very difficult continuous multimodal and multivariate nonlinear optimization problem,especially the unknown functions are discontinuous and cusps.To this end,a Chaotic Ant Swarm Optimization（CASO）based curve fitting with B-splines,called CASO-DF,is proposed to implement the smoothness fitting quickly.The approach is devised based on the curve fitting with B-splines using chaotic coordination of a single ant and self-organizing capacity of the whole ant colony.CASO-DF can adaptively adjust knots placement and choose the number of internal knots.Simulation results show that the proposed approach can perform effectively as well as efficiently,and this algorithm has better performance than other similar algorithms.

curve fitting;chaotic ant swarm optimization;knot placement;B-splines

A

TP18

10.3778/j.issn.1002-8331.1209-0312

XU Shanjian,GUO Youqiang,QI Xiaoming,et al.Chaotic ant swarm optimization in solving cu rve fitting with free knot B-sp lines.Computer Engineering and Applications,2014,50（16）：177-182.

安徽省自然科学基金（No.11040606M 151）。

徐善健（1973—），男，讲师，研究领域为数字信息处理，信息检索；郭有强（1966—），男，教授，硕士生导师，研究方向为网络信息处理、智能控制和优化算法；戚晓明（1975—），男，博士，副教授，研究方向为数字信息处理，信息检索；夏伟（1973—），男，博士，讲师，研究方向为形式化技术及应用，混杂系统理论及控制。E-mail：xiawei_0987@163.com

2012-09-26

2013-01-21

1002-8331（2014）16-0177-06

CNKI网络优先出版：2013-02-28,http://www.cnki.net/kcms/detail/11.2127.TP.20130228.1148.005.htm l