K-聚类的模糊神经网络对DO的控制研究

王彬，贠卫国

西安建筑科技大学信息与控制工程学院，西安 710055

K-聚类的模糊神经网络对DO的控制研究

王彬，贠卫国

西安建筑科技大学信息与控制工程学院，西安 710055

运用一种基于K-聚类算法的模糊径向基函数（RBF）神经网络对污水处理中的溶解氧质量浓度进行控制，该方法结合了模糊控制的推理能力强与神经网络学习能力强的特点，将模糊控制、RBF神经网络以及K-聚类学习算法相结合以在线调整隶属函数，优化控制规则。通过对阶跃输入仿真分析，其结果表明基于RBF的模糊神经网络控制器具有良好的动态性能、较强的鲁棒性和抗干扰能力，使其快速、准确地达到期望水平。

K-聚类算法；RBF神经网络；模糊控制；溶解氧；MATLAB仿真

1 引言

曝气池系统中的微生物都是好氧菌，要保证活性污泥系统正常运行，必须在混合液中保持一定浓度的溶解氧。溶解氧浓度过高，耗能太大；溶解氧浓度过低，丝状菌易于在系统中占优势，诱发产生污泥膨胀影响水质。因此如何把曝气池中溶解氧质量浓度控制在一个适当的水平是污水处理中研究的热点，传统的控制方式对溶解氧质量浓度的控制精度不高、实时性不够理想，缺乏一定的自适应能力。鉴于此，本文设计了一种基于K-聚类算法的模糊RBF神经网络控制器。

2 模型的确定

依据活性污泥法污水处理系统的基本原理及国际水协会废水生物处理设计与运行数学模型课题组建立的活性污泥1号模型（AMS1），并结合实际污水处理厂的性质和文献中的动力学参数[1-3]，确定污水处理厂的数学模型为：

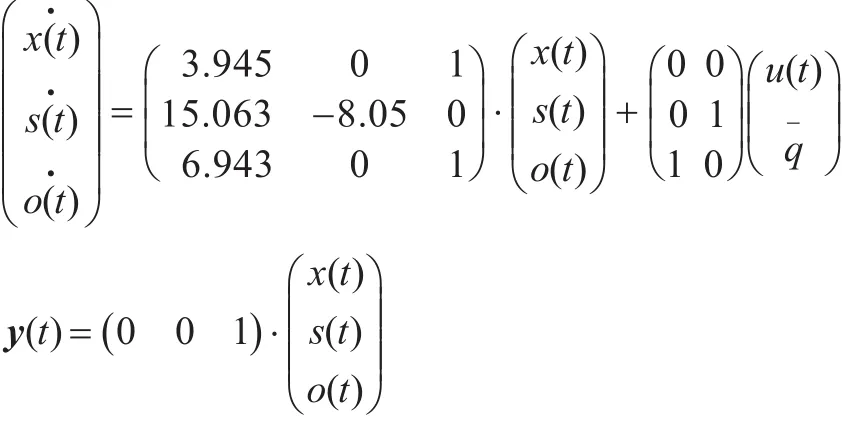
3 传统模糊控制器的设计

3.1 模糊控制器的结构

在图1中，r是溶解氧浓度给定输入，y是溶解氧浓度实际输出，e是给定值与实际输出值的偏差：e=r-y，E和EC分别是误差和误差变化的模糊量，u是模糊控制器输出量。

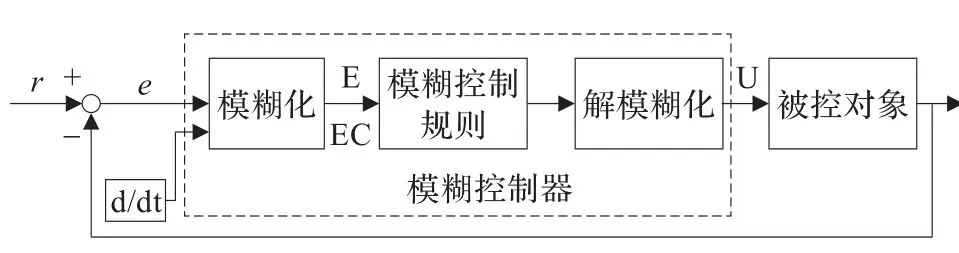
图1 模糊控制器结构图

3.2 量化因子的确定

根据污水处理工艺的要求，溶解氧浓度一般保持在2 mg/L，溶解氧浓度误差e和误差变化ec的物理论域分别为e=[-1.5，+1.5]，e=[-0.5，+0.5]。定义系统中误差、误差变化和输出控制量的离散论域均为[-6，6]，因此，利用量化因子求解公式并经过反复仿真修正，则可得到最终量化因子具体为：ke=1.2，kec=0.7，ku=0.5。

3.3 控制规则的确定

为保证溶解氧浓度的平稳性，隶属度函数采用平滑的高斯型隶属函数，并且根据溶解氧浓度调节的要求，对e和ec均取{PB（正大），PM（正中），PS（正小），ZO（零），NS（负小），NM（负中），NB（负大）}7个模糊子集，同时可确定模糊控制规则如表1。

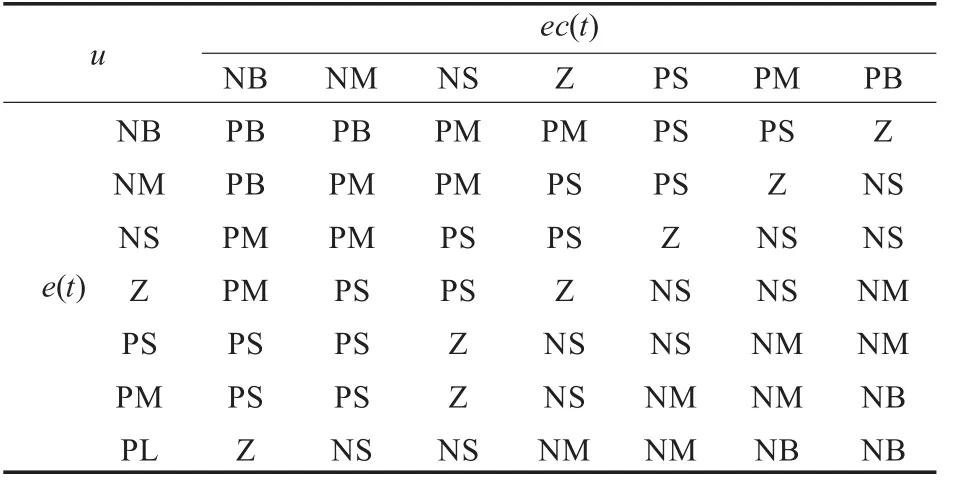
表1 模糊控制规则

4 模糊RBF神经网络控制器的设计

4.1 模糊RBF神经网络的结构

本文设计的模糊RBF神经网络共有4层。第1层为输入层，有2个节点。第2层为模糊化层，有7个节点。第3层为模糊推理层，有7个节点。第4层为输出层，有1个节点[4-6]。

下面为各层的具体描述，其中，fn(x)为各层的活化函数；n为层数，在这里n为1～4。

（1）输入层。该层起着将输入传送到下一层的作用。该层每个节点代表经过预处理过的输入变量，根据溶解氧浓度实际情况，将该层节点数设为2个，分别为溶解氧浓度误差和误差的变化，该层的输入为x1和x2，其中x1=e，x2=ec；活化函数为f1(x)=x。因此该层的输出为x1和x2。预处理过程是指将这两个实际连续变化量转化为(-6，6)之间的连续变化量。

（2）模糊化层。该层的功能是对输入量进行模糊化，求出各输入的隶属度。根据溶解氧浓度调节和控制要求，误差及误差变化率均取{NB，NM，NS，ZO，PS， PM，PB}7个模糊集合。因此，该层有7个节点。该层的输入为x1=e，x2=ec，选取高斯型函数作为隶属度函数进行模糊化。所以该层输出为：

其中，i=1，2；j=1，2，…，7。c和b分别为高斯函数的第i个输入变量的第j个模糊集合的隶属函数的中心和宽度。

（3）模糊推理层。该层有7个节点，它们各代表了一种模糊控制规则，通过表1的模糊控制规则和NAMDANI模糊推理方法，将上层中2个输入的模糊量经过两两相乘，得到这层的输出值。因此，本层的活化函数即输出为：

其中，i=1，2，…，7；j=1，2，…，7；f2(1，i)和f2(2，j)分别表示误差e及误差变化率ec对每个模糊集合的隶属函数，第2层和第3层的连接权值均为1。

（4）输出层。该层由1个节点构成，作用是实现清晰化计算，本文采用重心法来实现。对应的公式如下：

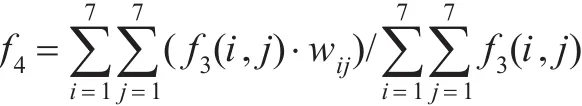
其中，i=1，2，…，7；j=1，2，…，7；上式中，wij是3层和4层的连接权值，如果对结论语言值也采用钟型函数，则就是该语言变量的中心值。

为了对比模糊控制和模糊RBF神经网络控制的性能，本文设定溶解氧浓度误差及误差变化的论域、模糊集合与模糊控制系统中均相同，模糊推理也采用NAMDANI推理方法，而清晰化过程也同样采用了重心法。

4.2 模糊RBF神经网络的学习算法

在本文中，AFNNC的输入量的隶属函数采用钟型分布，调整其中心值可改变其在论域上的分布位置，调节宽度即可改变其形状。而对于结论语言值，由于第3、4层的连接权值就是结论语言变量的中心值，因此调整就等效于调整其隶属函数[7]。

下面研究参数的调整问题，由于BP算法学习速率较慢，而且容易落入局部极小点，因此本文中采用了径向基函数中心和宽度运用K-聚类算法进行调节，权值运用梯度下降法进行调节的方法。

4.2.1K-m eans聚类算法

本文就是严格按以下的步骤编写算法程序进行在线训练。K-means聚类算法步骤主要如下所示：

（1）给定大小为N的数据集，令i=1，选取k个初始聚类中心Zj(i)，j=1，2，…，k。

（2）计算每个数据对象与聚类中心的距离D(Xi，Zj(i))。其中i=1，2，…，n，j=1，2，…，k，如果满足式（1）：则Xi∈Wk。

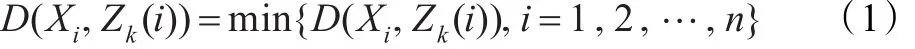
（3）计算K个新的聚类中心

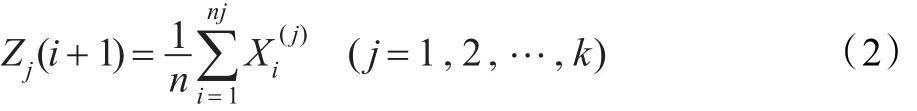
（4）判断：若Zj(i+1)≠Zj(i)，j=1,2,…，k，则i=i+1，返回（2），否则该算法结束。

整个算法的基本流程如图2所示。

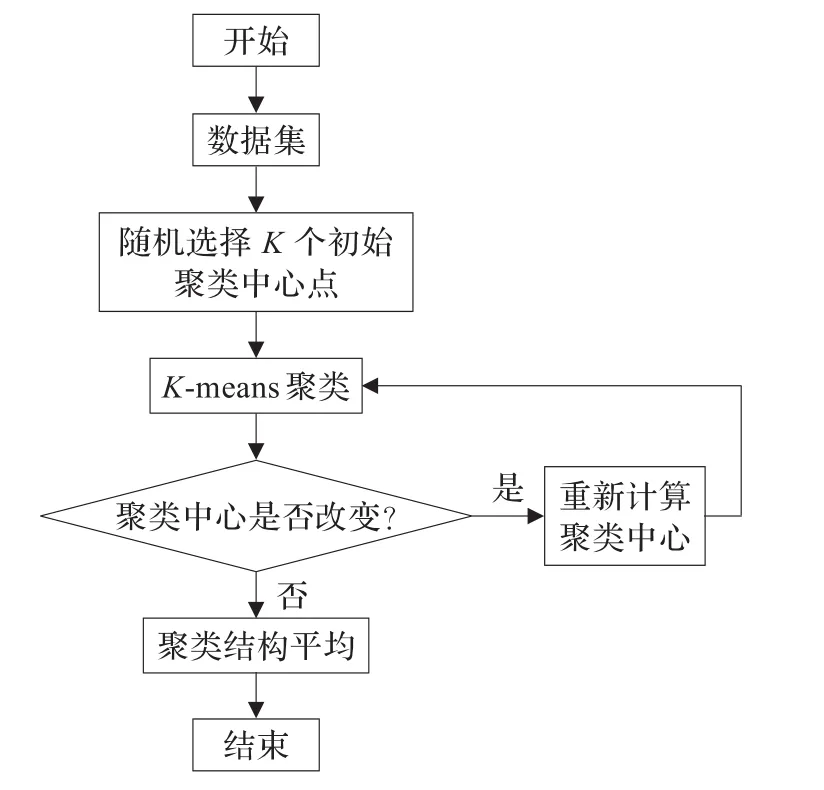
图2K-means算法的基本流程图

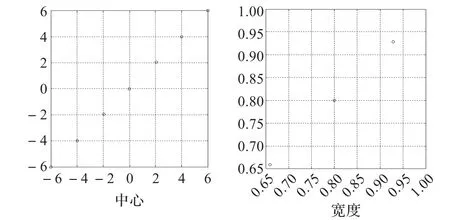
图3 中心和宽度的聚类结果

4.2.2 梯度下降法

在这里，用梯度下降法对神经网络输出层权值参数进行修正，则输出层的权值为：

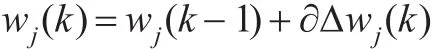
其中，∂为学习动量因子；k为迭代步骤。学习算法的关键就是计算Δwj(k)，学习方法如下：

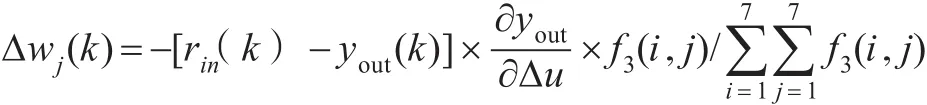
其中，∂为学习速率；wj就是输出节点与上一层各节点的连接权，j=1，2，…，49。

5 仿真研究

为了便于和传统的模糊控制效果进行对比，因此本文中首先进行的是模糊控制器的设计，应用MATLAB 2010（b）中.M文件对这种控制器性能以及抗干扰性进行仿真。

在仿真过程中，模糊RBF神经网络的输入信号为两个，即控制系统的误差信号和误差变化信号，针对每个输入取7个模糊集进行模糊化，即n=2，N=7，模糊RBF神经网络结构取2-7-7-1的形式，网络学习参数取η=0.3，α=0.1。量化因子为：ke=0.7，kec=0.6，ku=0.7。聚类循环条件为：dist＜0.1。

5.1 模糊控制系统仿真

图4所示为模糊控制器阶跃响应仿真曲线，阶跃输入为2 mg/L。从仿真曲线可以看出，在现有模糊控制模糊规则查询表条件下，模糊控制器阶跃响应具有较好的上升时间，稳态误差接近为零，但是超调量较为显著，过渡时间相对较长。因此说明模糊控制动态性能不太理想。

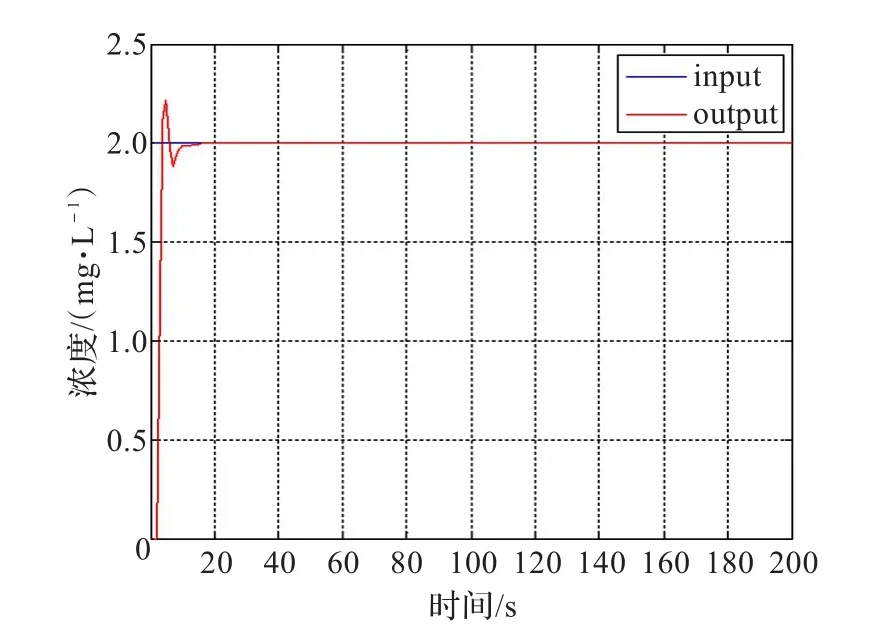
图4 模糊控制器阶跃响应仿真曲线

5.2 基于RBF网络的模糊神经控制系统仿真

设定阶跃变化为2 mg/L。从图5仿真曲线可以看出；基于RBF网络的模糊神经控制器的阶跃动态响应具有较好的上升时间，超调量接近为零，过渡时间较短为9 s，其稳态误差为0.000 1，与单纯模糊控制器阶跃响应相比动态性能要理想得多。

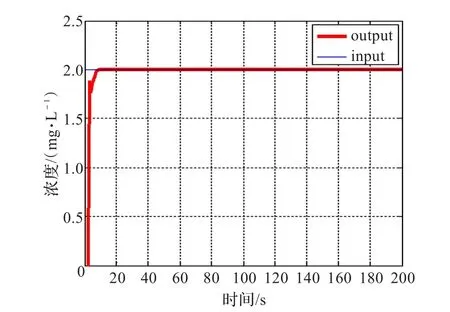
图5 基于RBF网络的模糊神经控制系统仿真

5.3 隶属函数在线动态变化仿真

图6可以看出传统模糊控制的隶属度函数曲线是固定不变的，而模糊RBF神经网络控制的隶属度函数曲线是自适应、在线动态调整的。因此无论在动态性能还是稳态性能上其控制效果均优于传统模糊控制。

图6 隶属函数在线动态变化仿真

5.4 变参数、加扰动的模糊RBF神经网络仿真

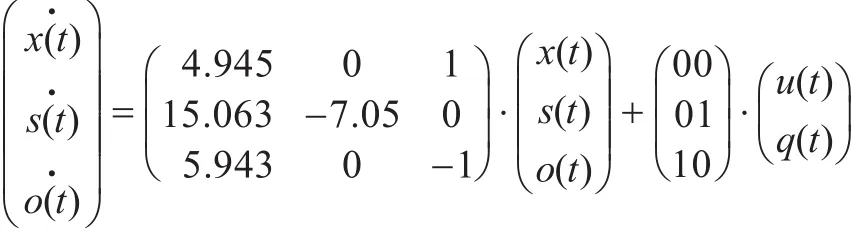
由图7仿真可以看出：在阶跃输入中加入干扰pluss= 0.05×(1-2×rand(1，1))和采用上述变化参数模型后，传统模糊控制的响应曲线很难精确地稳定在设定值2 mg/L，其阶跃响应曲线受扰动的影响较大，整个过程有较强的抖动。而模糊RBF神经网络的响应曲线能够快速准确地达到设定值2 mg/L，其阶跃响应曲线几乎不受扰动的影响，稳态误差几乎为0。表明其具有较强的抗干扰能力和鲁棒性能。

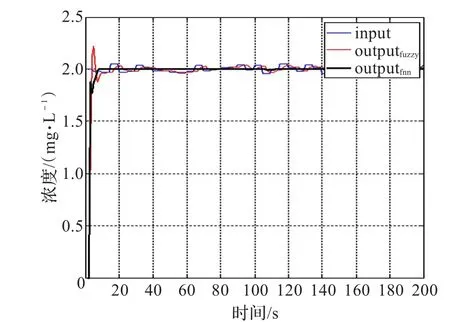
图7 变参数、加扰动的模糊RBF神经网络仿真

6 结论

本文将K-聚类算法与模糊RBF神经网络相结合避免了梯度下降法中学习速率慢，易陷入局部极小点等缺点，通过对带扰动的不同参数的污水系统模型进行仿真试验，均得到了良好的控制效果。实验研究结果表明该模糊神经网络控制器具有以下性能：

（1）控制精确，拥有极强的抗干扰能力，能够减少对执行元件的冲击损害。

（2）具有较好的自适应，能够满足参数在允许范围内的变化要求，以及较强鲁棒性。

[1]Feng Yuzhao，Long Tengrui，Guo Jingsong，et al.Optimal robustness control method of activated sludge system based on uncertain parameters[J].China Water＆Wastewater，2003，19（3）：14-16.

[2]Orhon D，A rtan N.Modelling of activated sludge system[M]. Lancaster，PA，USA：Technomic Publisher Co，1994.

[3]陈兆波，陈志强，林海龙.污水处理系统数学模型[M].哈尔滨：哈尔滨工业大学出版社，2009.

[4]胡玉玲，冉维丽，乔俊飞.污水处理过程中DO的模糊神经网络控制[J].计算技术与自动化，2003，22（2）：68-71.

[5]李国勇.智能控制及其MATLAB实现[M].北京：电子工业出版社，2005.

[6]包枫，赵鹤鸣，陈静.SBR系统中的模糊神经网络控制器设计[J].计算机工程，2010，36（8）：203-205.

[7]刘超彬，乔俊飞，张芳芳.污水处理过程中溶解氧的模糊神经网络控制[J].山东大学学报：工学版，2005，35（3）：83-87.

WANG Bin,YUN Weiguo

Information and Control Engineering Institute,Xi’an University of Architecture and Technology,Xi’an 710055,China

Using a fuzzy Radial Basis Function（RBF）neural network based onK-clustering algorithm controls the concentration of quality of the dissolved oxygen（do）in the sew age treatment.This method combines fuzzy control reasoning ability and neural network learning ability characteristic.Fuzzy control,RBF neural network andK-clustering learning algorithm are applied in order to adjust subjection function on-line,optimize control rules.By the step input simulation analysis,the results show that fuzzy neural network controller based on the RBF has a good dynamic performance,strong robustness and anti-interference ability,make it fast and accurately to achieve the desired level.

K-the clustering algorithm;RBF neural network;fuzzy control;Dissolved Oxygen（DO）;MATLAB simulation

A

TP183

10.3778/j.issn.1002-8331.1209-0057

WANG Bin,YUN Weiguo.K-C lustering fuzzy neural network to DO control research.Computer Engineering and Applications,2014,50（16）：150-153.

王彬（1987—），男，硕士研究生，主要研究方向为智能控制理论、方法、应用等。E-mail：w b19871226@163.com

2012-09-10

2012-12-03

1002-8331（2014）16-0150-04

CNKI网络优先出版：2012-12-18,http://www.cnki.net/kcms/detail/11.2127.TP.20121218.1520.007.htm l