内逆Pρ-集合与其概率特征

2014-07-07张曰云于秀清

计算机工程与应用 2014年16期

关键词：山东大学理学学报

张曰云，于秀清

德州学院数学科学学院，山东德州 253023

◎数据库、数据挖掘、机器学习◎

内逆Pρ-集合与其概率特征

张曰云，于秀清

德州学院数学科学学院，山东德州 253023

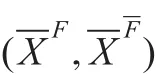
内逆P-集合内；逆Pρ-集合；元素迁移；概率特征

1 引言

2008年，史开泉教授把动态特性引入普通集合X，给出P-集合[1-2]（packet sets）的概念与结构。P-集合是由内P-集合（internal packet set）与外P-集合XF（outer packet setXF）构成的集合对；或者(，XF)是P-集合。汤积华、林宏康等给出了P-集合理论在信息系统等领域的应用[3-10]，于秀清、张凌等将元素迁移的随机特性引入P-集合，提出随机P-集合的概念[11-14]，随机P-集合是P-集合的扩展，P-集合是随机P-集合的特例，随机P-集合的提出扩大了P-集合理论的应用范围，2012年，史开泉在P-集合的研究基础上，提出了P-集合的反问题逆P-集合[15]；逆P-集合是由内逆P-集合（internal inverse packet set）与外逆P-集合（outer inverse packet set）构成的集合对，即)是逆P-集合。逆P-集合具有与P-集合相反的动态特征：给定集合X，α是X的属性集合，若在α内补充一些属性，α变成αF，α⊆αF，集合X变成内逆P-集合，X⊆；同时，在α内删除一些属性，α变成⊆α，集合X变成外逆P-集合⊆X；与构成的集合对是逆P-集合；闫立梅、赵树理等在对P-集合理论进行了深入研究的基础上，给出逆P-集合在未知信息推理-搜索与发现、信息智能融合-过滤辨识等方面的应用[16-20]。

为了更容易接受本文的研究结果，在第2章中，简要介绍了逆P-集合的概念与结构，关于逆P-集合与P-集合的更多更详细的讨论与应用见文献[1，2，15-20]。

2 逆P-集合及结构

文献[15]给出：

给定有限普通集合X={x1，x2，…，xq}⊂U，α={α1，α2，…，αk}⊂V是X的属性集合；称-XF是X生成的内逆P-集合（internal inverse packet set），简称-XF是内逆P-集合，而且

X+称作X的F-元素补充集合，而且

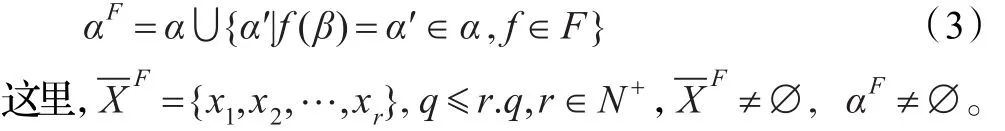
如果集合X的属性集合α内的属性不断被补充，得到

由式（7）得到内逆P-集合串

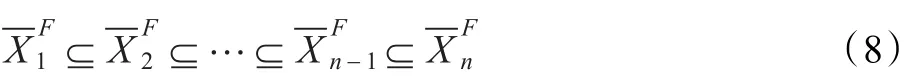
如果集合X的属性集合α内的属性不断被删除，得到

式（11）是逆P-集合的对族的形式，是逆P-集合的一般形式；I，J是指标集合。

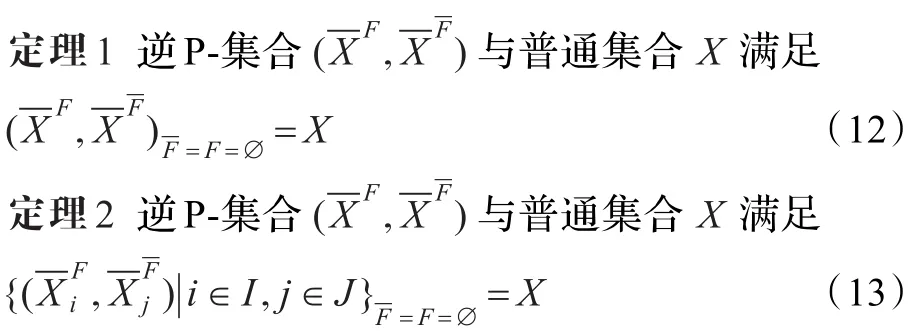
3 元素迁移概率与内逆Pρ-集合生成

定义1设元素集合X={x1，x2，…，xq}⊂U，对于元素u∈U但u∈X，称f(u)=x∈X发生的可能性大小是元素迁移f的概率，记作

这里，pF(f)∈[0，1]。

定义2设属性集合α={α1，α2，…，αr}⊂V，对于属性β∈V，但，称f(β)=α′∈α发生的可能性大小是属性迁移f的概率，记作

这里，p′F(f)∈[0，1]。

这里，pF(f(u)=x∈X)≥ρ表示：对于x∈X，，f∈F把u变成f(u)=x∈X的概率大于或等于ρ，≠。

如果-XpF的属性集αp′F，αp′F与集合X的属性集α满足

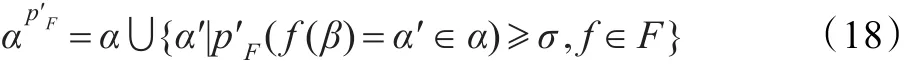
这里，p′F(f(β)=α'∈α)≥σ表示：对于β∈V，β∈α，f∈F把β变成f(β)=α′∈α的概率大于或等于σ，αp′F≠。

定义4ηpF称作内逆Pρ-集合关于集合X依概率pF(f)生成的外包度，如果

根据定义（1）～（4）可得

命题1对∀f∈F，若p′F(f)≡0，则对∀σ∈[0，1]，有αp′F=α；反之成立。

命题2对∀f∈F，若pF(f)≡1，则对∀σ∈[0，1]，有αp′F=αF；反之成立。

命题3属性集合α，αp′F，αF满足

命题4若ηpF是内逆Pρ-集合生成的外包度，则

定理3（内逆Pρ-集合第一动态关系）对于∀ρ∈[0，1]，集合X，满足

推论1对∀f∈F，若pF(f)≡0，则对∀ρ∈[0，1]，有

推论2对∀f∈F，若pF(f)≡1，则对∀ρ∈[0，1]，有

定理4（内逆Pρ-集合第二动态关系）对∀f∈F，∀ρ∈[0，1]，有

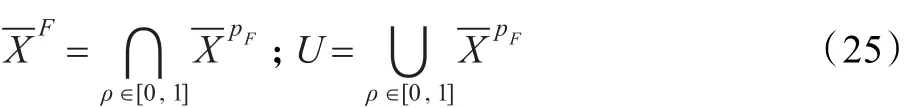
定理5（内逆Pρ-集合的不可辨识关系）对∀f∈F，若p(f)≡1，则对∀ρ∈[0，1]，有

上述证明过程是可逆的，所以充分性成立，故定理5成立。

根据定理3与定理5，可以得到结论：内逆Pρ-集合是内逆P-集合与集合X的扩展，内逆P-集合与集合X是内逆Pρ-集合的特例。

定理6（内逆Pρ-集合的可辨识定理）若ηpF是生成的外包度，则ηpF＞1的充要条件是：

4 内逆Pρ-集合的概率特征

定义7称{Ii|i=1，2，…，n;n∈N+}是概率区间[0，1]的有限分割，如果满足以下条件：

1°对任意Ii，Ij满足Ii∩Ij=，i≠j，i，j=1，2，…，n。

定理7（内逆Pρ-集合与元素迁移概率关系定理）设ρ1、ρ2是元素迁移的概率，且0≤ρ1＜ρ2≤1，则

证明：由0≤ρ1＜ρ2≤1知集合X的补充集合满足关系：

推论6设(σi，i=1，2，…，n)是属性迁移概率，且0≤σ1≤…≤σi≤…≤σn≤1，内逆Pρ-集合的属性集合为，则对∀ρ∈[0，1]有

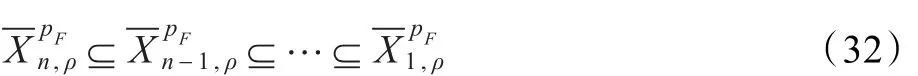
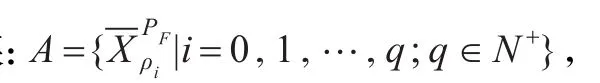
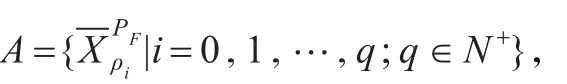
类似于离散随机变量概率分布，由定理10及推论7可知当ρ在区间[0，1]分割的子区间上取值时，内逆Pρ-集合保持不变。

5 讨论

逆P-集合是P-集合的反问题，它的提出解决了一类利用P-集合无法解决的问题，本文将概率论的知识与内逆P-集合相融合，给出了内逆Pρ-集合的概念与结构，扩展了内逆P-集合理论，使得逆P-集合在信息系统中有了更广泛的应用。

[1]史开泉.P-集合[J].山东大学学报：理学版，2008，43（11）：75-84.

[2]SHI Kai-quan.P-sets and its applications[J].An International Journal Advances in Systems Science and Applications，2009，9（2）：209-219.

[3]史开泉.P-集合，逆P-集合与信息智能融合-过滤辨识[J].计算机科学，2012，39（4）：1-13.

[4]SHI Kai-quan，LI Xiu-hong，Camouflaged information and its on identification and its applications[J].An International Journal Advances in Systems Science and Applications，2010，10（2）：208-216.

[5]史开泉.P-集合与它的应用特征[J].计算机科学，2010，37 （8）：1-8.

[6]汤积华，陈保会，史开泉.P-集合与(，F)-数据生成-辨识[J].山东大学学报：理学版，2009，44（11）：19-25.

[7]于秀清.迭代F-内嵌入信息生成与它的遗传发现-应用[J].系统工程与电子技术，2011，13（12）：2691-2795.

[8]Li Hong-kang，Li Yu-ying.P-sets and its P-separation theorem s[J].An International Journal Advances in Systems Science and Applications，2010，10（2）：209-215.

[9]于秀清.F-数据簇与缺损数据修复-还原[J].计算机工程与应用，2013，49（6）：139-142.

[10]周玉华，张冠宇，张丽.内外数据圆与动态数据发现[J].山东大学学报：理学版，2010，45（8）：21-26.

[11]于秀清.P(α，β)-集合与它的随机特性[J].计算机科学，2010，37（9）：218-221.

[12]汤积华，张凌.内P-集合的概率特性[J].龙岩学院学报，2009，27（5）：19-21.

[13]于秀清，董立华，侯玉梅，等.外PpF(f)-集合及其概率特征[J].山东大学学报：理学版，2010，45（9）：45-56.

[14]于秀清.内pρ-集合与元素迁移概率特征-应用[J].计算机工程与应用，2012，48（3）：49-52.

[15]史开泉.逆P-集合[J].山东大学学报：理学版，2012，47（1）：98-103.

[16]闫立梅，逆P-推理与未知信息推理-搜索与发现[J].计算机科学，2012，39（8）：268-272.

[17]史开泉.逆P-集合与信息智能融合挖掘-发现[J].山东大学学报：理学版，2013，48（8）：97-103.

[18]汤积华，陈保会，张凌，等.函数逆P-集合与逆P-信息规律动态分[J].山东大学学报：理学版，2013，48（8）：104-110.

[19]张景晓，徐风生.函数内逆P-集合在QSPR研究中的应用[J].山东大学学报：理学版，2013，48（8）：92-96.

[20]赵树理，王军昌，史开泉.逆P-等价类的逆P-推理分离-还原[J].山东大学学报：理学版，2013，48（1）：62-67.