基于差分进化算法的认知无线电频谱分配

毕晓君，李安宁

哈尔滨工程大学信息与通信工程学院，哈尔滨 150000

基于差分进化算法的认知无线电频谱分配

毕晓君，李安宁

哈尔滨工程大学信息与通信工程学院，哈尔滨 150000

针对认知无线电系统中认知用户分配可用频谱问题，提出基于差分进化算法的认知无线电频谱分配算法。利用差分算法设置参数少、寻优能力强、不易于陷入局部最优等特点，得到可以使认知用户平均系统效益最大化的频谱分配方案。仿真结果表明，提出的算法不仅提高了用户平均系统效益，而且缩短了运行时间，提高了频谱分配效率。

认知无线电；认知用户；差分进化算法；频谱分配；系统效益

1 引言

近几年随着人们对无线通信需求的增长，无线频段不断被授权用户分配，造成频谱日益拥挤，因此出现了认知无线电技术，以期在授权频段中寻找频谱空穴，提高频谱的利用率[1]。在认知无线电网络中[2-3]，频谱分配是一项关键技术，它允许未授权的无线系统通过对周围无线通信环境的感知，来实现共享授权用户所使用的频段，从而达到提高频谱利用效率的目的。因此，频谱分配方案的好坏将直接影响整个系统的资源利用率[4-5]。对此，已有学者进行了相关研究，其中应用效果最好的是基于改进遗传算法的频谱分配算法[6]，虽然可以在一定程度上提高用户平均效益，但是遗传算法自身存在易于陷入局部最优的缺点，无法保证每次都能获得最佳的频谱分配方案。差分进化算法是近年兴起的效果最好的优化算法，具有设置参数少、寻优能力强、不易于陷入局部最优等优点[7-8]，为此本文提出一种基于二进制差分进化算法的频谱分配算法，可以在更短的时间内得到用户效益更高的分配方案。

2 认知无线电频谱分配模型

认知无线电的频谱分配模型由可用频谱矩阵、效益矩阵、干扰矩阵和无干扰分配矩阵来描述[9]。假设分配周期相对于频谱环境变化时间很短，那么分配周期内各矩阵将保持不变[10]，假设在小区内某一时刻有N个认知用户需要通信，同时有M个空闲频带可以使用，则相关矩阵具体定义如下：

（1）可用频谱矩阵L

L={ln，m∈{0，1}}N×M，如果ln，m=1表示用户n可以使用频段m，ln，m=0表示用户n不可以使用频段m。具体的含义是如果频谱m被授权用户占用，一旦有认知用户使用频谱m则会对授权用户产生干扰，违背认知无线电在不干扰授权用户基础上提高频谱使用率这一初衷，因此分配方案需要根据可用矩阵L来进行分配。

（2）效益矩阵B

B={bn，m}N×M，bn，m表示认识用户n使用频谱m为系统所带来的效益。由于不同的认知用户采用的发射功率、调制技术等不同，因此在不同的频谱上具有不同的系统效益，如频谱利用率、最大流量。由于只有可用的频谱才会为系统带来效益，因此，当ln，m=0时，必有bn，m=0。

（3）干扰矩阵C

各个次用户之间由于使用相同的可用频谱而会对彼此产生干扰，用矩阵C表示，C={cn，k，m∈{0,1}}N×N×M。认知用户n和k(1≤n，k≤N)同时使用频谱m(1≤m≤M)产生干扰表示为cn，k，m，反之，cn，k，m=0。C由L决定，当n=k时，cn，n，m=1-ln，m；亦需满足cn，k，m≤ln，m×lk，m，即频谱m如果同时对认知用户n和k可用时，就会可能产生干扰。

（4）无干扰分配矩阵A

将可用、无干扰的频谱分别分配给用户，得到A= {an，m|an，m∈{0，1}}N×M，其中an，m=1表示将频谱m分配给认知用户n，反之，an，m=0。同时，矩阵A必须满足C定义的如下约束条件：

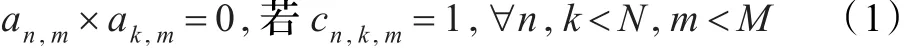
文献[6]选择最大化系统效益总和（MSR）工作目标，其目的是使整个小区内所有认知用户取得的效益总和最大化，然而当认知用户逐渐增多时并不能很好地反映系统中平均每个认知用户所取得的系统效益，为了体现出系统中认知用户平均系统效益U，本文选取认知用户平均系统效益作为工作目标[11]，具体公式如式（2）所示。

其中，N为认知用户的数目，M为可用频谱的数目。

3 差分进化算法

3.1 标准差分进化算法

差分进化算法（Differential Evolution，DE）是1995年由Storn等人提出的一种群体智能优化算法[12]，2005年被引入国内。DE算法具有记忆个体最优解和种群内信息共享的特点，通过种群内个体的合作与竞争来实现对优化问题的求解[13]，其本质是一种基于实数编码的具有保优思想的贪婪遗传算法。

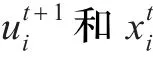
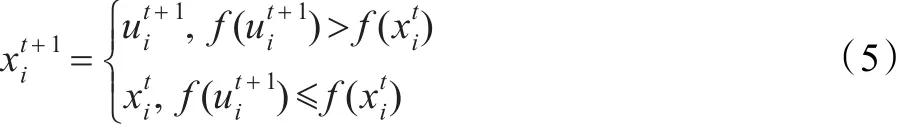
其中f为目标函数。

3.2 二进制差分进化算法

最初的DE算法主要针对解决连续空间函数优化问题，为解决离散优化问题，文献[14]提出一种二进制差分算法（Binary Differential Evolution，BDE），可以有效解决离散函数优化问题。

与标准差分算法不同之处在于问题解空间都是通过0和1编码，如果直接进行变异操作所得到的变异个体可能不符合解空间取值范围的限制，所以进行以下操作，首先按照下式对解向量映射到[0，1]之间，如公式（6）所示。

然后针对变异操作后不在[0，1]之间的解按照sigmoid函数映射到该范围内，如公式（7）所示。

最后在交叉操作之前再将解重新映射成由0和1组成的解，如公式（8）所示。

除了以上不同之外，二进制差分算法与标准差分算法完全相同。

4 基于BDE算法的认知无线电频谱分配算法

本文研究的认知无线电频谱分配问题可以描述为：在L，B，C已知的情况下，如何找到最优的无干扰分配矩阵A，使得认知用户平均系统效益达到最大化。通过研究发现本文的频谱分配问题可以归结为NP问题，而差分进化算法是近年解决复杂NP问题较为理想的方法，因此本文首次将BDE算法应用到频谱分配问题中，对公式（2）进行寻优，使U最大。在求解过程中，首先需要根据矩阵L生成初始种群，如果可用频谱矩阵L中的ln，m为0，则对应无干扰分配矩阵A中相同位置的an，m必然为零，因此可以选择对L中值为1位置对应A中的元素位置进行编码，编码长度等于L中值为1的个数l，因此种群中个体是长度为l的一维矢量[15]；在利用公式（2）计算个体目标函数值时，需要对两个矩阵对应元素相乘，因此需要将种群中个体映射成无干扰分配矩阵A，只需先将一维矢量中元素为零对应矩阵L中相应位置元素值置为0，其他保持不变得到矩阵A1，再利用公式（1）对所得到的矩阵进行约束处理，即得到矩阵A。图1给出了N=5、M=5时代表可行解的进化个体编码结构示例，由图中可以得到矩阵L中元素值为1的个数为7，种群个体pi为随机生成长度为7的一维矢量，在计算个体目标函数值前，将pi中值为0元素对应矩阵L中相应位置元素值置0，得到矩阵A1，再利用矩阵C通过公式（1）进行约束处理，可得到无干扰分配矩阵A。

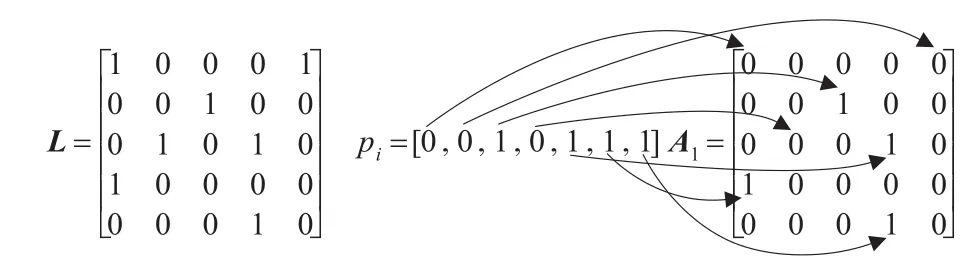
图1 差分进化个体编码结构示例

算法的实现流程如下：

（1）为了模拟实际应用中各个认知用户使用频谱所带来的效益和不同用户之间可能存在的干扰，随机生成可用频谱矩阵L、效益矩阵B（本文在创建B时给B乘以了一个系数M/N，用来模拟小区无线网络的实际情况）、干扰约束矩阵C。

（2）设定参数：设定种群规模popsize，算法迭代次数max_g，交叉概率CR，变异因子F，并根据可用频谱矩阵L确定初始种群中每个个体的维数codelength。

（3）生成初始种群：随机生成一个popsize行codelength列的矩阵，其中每一行代表一个个体。

（4）计算目标函数值：按照图2求解得到矩阵A1；并对A1利用公式（1）进行约束处理，使其满足无干扰约束条件；再根据公式（2）计算得到每个个体的目标函数值。

（5）差分和交叉算子操作：从父代种群中随机选取两个不同的个体，根据公式（3）产生变异后新的子代；根据公式（4）生成交叉后的新个体。

（6）选择操作：使变异和交叉前后的个体进行适应度比较，目标函数值大的个体保留下来进入下一代。

（7）重复步骤（4）～（6），直到满足终止条件。其中适应度值最大的解映射成的矩阵就是使用户平均系统效益达到最大的无干扰分配矩阵。

算法时间复杂度是影响算法效率的重要因素，通过算法的实现流程可以分析得到本文算法时间复杂度包括计算频谱分配模型矩阵的时间复杂度和执行种群迭代的时间复杂度，频谱分配模型矩阵的时间复杂度为O(N2M)，执行种群迭代的时间复杂度为O(popsize×N2M)，因此BDE算法迭代一次的时间复杂度为O(popsize×N2M)。

5 实验仿真与结果分析

为验证本文提出算法的效果，这里进行了仿真实验，并与目前效果最好的改进遗传算法[6]进行对比实验。仿真结果均由算法重复运行30次并计算平均值而获得，从而验证本文提出算法的有效性和先进性。实验是在Inter core i7 CPU Q720，1.6 GHz、内存4 GB的计算机上运行，程序采用MATLAB 2010b版本编写。

系统仿真实验所用到的相关参数如下：种群规模popsize=10，迭代次数max_g=500，改进遗传遗传算法中pc1=0.6，pc2=0.9，在BDE算法中CR=0.8，F=0.05。

本文分别从用户平均系统效益随迭代次数变化曲线、随认知用户数目变化曲线和随频谱数目变化曲线三方面将本文BDE算法与改进遗传算法进行对比。

图2给出了M=10、N=10时，两种算法系统效益随迭代次数的变化曲线。

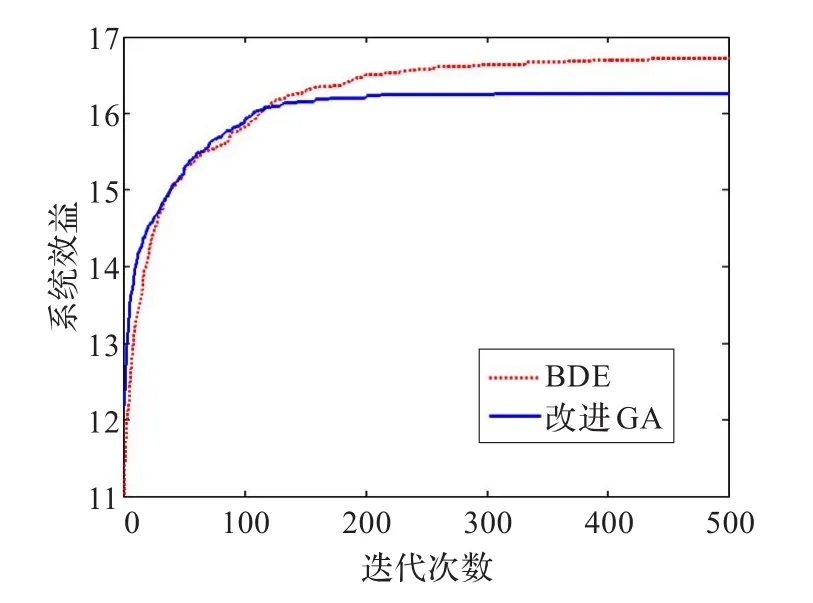
图2 用户平均系统效益变化曲线

从图中可以看出本文提出频谱分配算法迭代最后能够获得的系统效益远远高于改进遗传算法获得的系统效益。

在实际应用中，频谱分配要求算法必须在较快的时间内得到分配方案，因此要求算法的运行时间要短，在M=10、N=10时，改进遗传算法所需运行时间为1.8 s，本文的BDE算法所需运行时间为1.4 s，可以看出本文算法的运行时间要少于改进遗传算法，说明本文提出的算法不仅为认知用户带来更高的系统效益，而且花费的时间更短。两个算法达到相同精度时，本文BDE算法所需迭代次数和时间均少于改进遗传算法，说明BDE算法收敛速度快于改进遗传算法。

在实际无线环境中，频谱数目和认知用户数目实时改变，并且数目可能较大，需要分别验证用户平均系统效益随频谱数目和认知用户数目变化时的工作性能。

图3给出了认知用户数目固定，系统效益随频谱数目的变化曲线，具体参数为N=10，M从10逐渐变化到30。

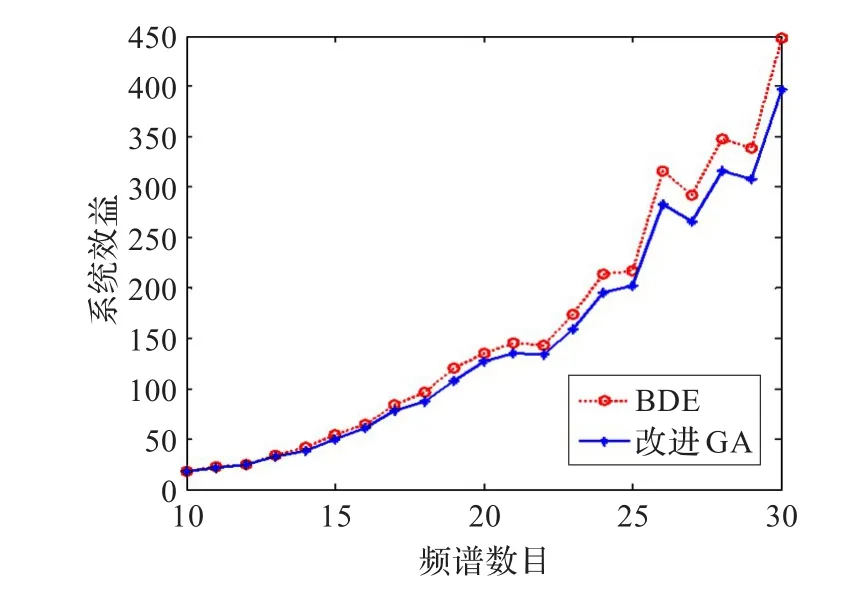
图3 用户平均系统效益变化曲线

从图中可以看出随着频谱数目增多，用户平均系统收益呈总体上升趋势，而本文BDE算法所取得的系统综合收益始终要高于基于改进遗传算法的系统收益，说明本文算法在大规模频谱数量分配问题中可以获得更好的频谱分配方案。

图4给出了频谱数目固定，认知用户平均系统效益随认知用户数目的变化曲线，具体参数为M=10，N从10逐渐变化到30。

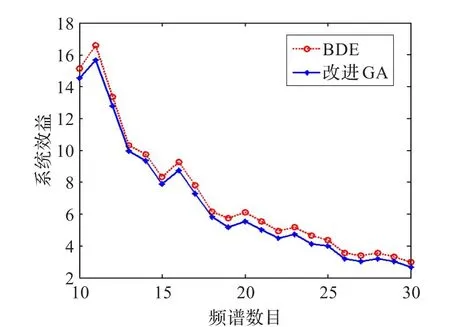
图4 用户平均系统效益变化曲线

从图中可以看出随着认知用户的数目增多，用户平均系统收益呈总体下降趋势，而本文BDE算法所取得的认知用户平均系统收益始终要高于基于改进遗传算法的系统收益，说明在为大规模认知用户频谱分配问题中，本文算法可以获得更好的频谱分配方案。

6 结论

针对认知无线电频谱分配算法存在算法收敛速度慢，易陷入局部最优等缺陷，本文提出了一种基于差分进化算法的频谱分配算法，充分利用差分进化算法具有设置参数少、寻优能力强、不易于陷入局部最优等优点，得到可以使认知用户平均系统效益最大化的频谱分配方案。实验仿真结果表明，本文提出的算法收敛速度快，可使用户获得更高的系统效益，并且在大规模频谱数量分配问题和大规模认知用户频谱分配问题中可取得更好的分配结果，在认知无线电系统中具有一定的实用价值。

[1]王臣昊，杨震，肖小潮.基于优化贝叶斯压缩感知算法的频谱检测[J].信号处理，2012，28（5）：750-756.

[2]王钦辉，叶保留，田宇，等.认知无线电网络中频谱分配算法[J].电子学报，2012，40（1）：147-154.

[3]滑楠，曹志刚.认知无线电网络路由研究综述[J].电子学报，2010，38（4）：910-918.

[4]Wen K，Fu L S，Li X S.Genetic algorithm based spectrum allocation for cognitive radio networks[C]//2011 International Conference on Coputer，Communication，Control and Automation.Zhuhai，China，19-20 November，2011：693-700.

[5]Zhao Z J，Peng Z，Zheng S L，et al.Cognitive radio spectrum allocation using evolutionary algorithms[J].IEEE Trans on Wireless Communications，2009，8（9）：4421-4425.

[6]朱冰莲，裴光术，张磊，等.认知无线电网络中系统效益最大化的频谱分配[J].计算机工程，2012，38（3）：107-109.

[7]杨启文，蔡亮，薛云灿.差分进化算法综述[J].模式识别与人工智能，2008，21（4）：506-513.

[8]刘若辰，焦李成，雷七峰，等.一种新的差分进化约束优化算法[J].西安电子科技大学学报，2011，38（1）：47-52.

[9]Bernaille L，Teixeira R，Akodkenou I.Traffic classification on the fly[J].Computer Communication Review，2006，36（2）：23-26.

[10]张北伟，朱云龙，胡琨元.基于粒子群算法的认知无线电频谱分配算法[J].计算机应用，2011，32（12）：3184-3214.

[11]Peng C，Zheng H，Zhao B Y.Utilization and fairness in spectrum assignment for opportunistic spectrumacess[J]. ACM Mobile Networks and Applications，2006，11（4）：555-576.

[12]毕晓君，王义新.多模态函数优化的拥挤差分进化算法[J].哈尔滨工程大学学报，2011，32（2）：223-227.

[13]王培崇，钱旭，王月，等.差分进化算法研究综述[J].计算机工程与应用，2009，45（28）：13-16.

[14]Deng C S，Zhao B Y，Yang Y L，et al.Novel binary differential evolution algorithm for discrete optimaization[C]//5th International Conference on Natural Computation，Tianjian，China，14-16 August 2009：346-349.

[15]彭振，赵知劲，郑仕链.基于混合蛙跳算法的认知无线电频谱分配[J].计算机工程，2010，36（6）：210-217.

BI Xiaojun,LI Anning

College of Information and Communication Engineering,Harbin Engineering University,Harbin 150000,China

According to the problem of spectrum allocation for secondary users in cognitive radio system,this paper puts forward the spectrum allocation algorithm based on the differential evolution algorithm.With less parameters,strong ability of finding global optimization solution and avoiding getting into local optimality of the differential evolution algorithm. The spectrum allocation scheme is got which can maximize the mean system utility.The simulation results show that the algorithm in this paper not only increases mean system utility of secondary users but also shortens running time and improves the efficiency of spectrum allocation.

cognitive radio;secondary user;DE algorithm;spectrum allocation;system utility

A

TN914

10.3778/j.issn.1002-8331.1209-0287

BI Xiaojun,LI Anning.Spectrum allocation based on differential evolution algorithm in cognitive rad io.Computer Engineering and Applications,2014,50（16）：100-103.

国家自然科学基金（No.61175126）；中央高校基本科研业务费专项资金（No.HEUCFZ1209）；教育部博士点基金（No.20112304110009）。

毕晓君（1964—），女，博士，教授，主要研究领域为智能信息处理；李安宁（1987—），男，硕士研究生，主要研究方向为智能信息处理，认知无线电。E-mail：bixiaojun@hrbeu.edu.cn

2012-09-25

2012-11-16

1002-8331（2014）16-0100-04

CNKI网络优先出版：2013-03-26,http://www.cnki.net/kcms/detail/11.2127.TP.20130326.1042.013.htm l