路径诱导系统中双向启发式A*算法研究

杨泳，户佐安，何金海

西南交通大学交通运输学院，成都 610031

路径诱导系统中双向启发式A*算法研究

杨泳，户佐安，何金海

西南交通大学交通运输学院，成都 610031

针对实际城市交通路网最优路径规划中存在的计算效率问题，研究了最优路径算法的快速实现技术，提出了一种双向启发式A*诱导算法。在分析经典Dijkstra算法和A*启发式搜索算法的基础上，利用双向A*算法分解搜索空间，采用完全二叉堆结构来实现计算过程中数据的存取，从而提高了算法的执行效率。实际路网仿真结果证明了该算法的优异性能。

最优路径规划；双向启发式A*算法；路网；二叉堆

1 引言

路径诱导是智能交通的研究热点，是交通流分配、物流配送、智能停车、车辆导航、集成电路设计等领域的基本问题，而网络中两点之间的路径诱导问题可以归纳为图论中计算求解带权有向图的最优路径问题。由于诱导系统实时性要求高、实际路网的规模庞大，而诱导计算机的处理能力和系统的存储资源有限，从而要求诱导算法的执行效率很高，甚至可以牺牲一些算法的精度。即使算法求得的最优路径解并非传统意义上的“最优”，是有一定偏差的次优解，但是只要能满足实际交通信息瞬时多变的实时性要求，同样能吻合客户交通出行的需求[1]。

在计算能力确定的前提下，主要有三种算法的优化策略[2]：存储数据结构优化、诱导算法优化及分层技术控制路网规模优化。杨瑜君[3]针对超大路网下最短路径问题展开研究，指出城市路网道路等级特性平缓，不适合采用分层技术。刘张雷[4]基于对Dijkstra、A*、D*Lite等几种算法对比分析提出一种基于路网变化的跳变动态路径规划策略，提高诱导效率。张玲[5]提出一种改进的Floyd最短路径算法来求解动态路径诱导系统中的“多准最优路径”问题。王士同[6]率先提出随机产生系统的双向启发式图搜索算法并证明其可行性。郑年波[7]通过改进传统的Dijkstra算法，提出基于搜索节点的双向启发式A*算法，并通过小范围路网算例实验表明该算法在效率和结果方面均能满足车辆导航及路径规划的要求。孙小荣[8]以Dijkstra算法和A*启发式算法为基础，结合双向A*算法和分层技术证明双向A*算法效率的优越性，同时指出最佳分层结构的弊端。本文在经典Dijkstra算法的基础上，结合优先队列数据结构，研究一种高效的双向启发式A*算法搜索策略。

2 算法描述

2.1 用堆实现路网存储结构

表示路网的数据结构有很多，例如邻接矩阵、邻接表、十字链表、队列等。然而实际路网的结构属于典型的边稀疏网络，表示路网的数据结构中最有效的是二叉堆[2]。W illioms在1964年提出了堆排序方法，该方法引入“堆”这种特定的数据结构。这里堆结构可以被视为一棵完全二叉树，可以作为高效的优先级队列来使用。本文在计算过程中，采用优先级队列与完全二叉树相结合的存储方式，实现双向启发式A*诱导算法。

2.2 最短路径问题数学描述

最短路径问题是指在一个带权值的图中找出两个指定节点间的一条权值和最小的路径。数学上，将交通道路网络的拓扑关系模型记为赋权有向图G=(N，A)。其中，节点N={i}，节点数n=|N|，弧集A={a|a=(i，j);i，j∈N}，弧数m=|A|，对任意弧度a=(i，j)，定义ca或ci，j为路段权值，满足ci，j＞0。对G中任意路径P=(a1，a2，…，al-1，al)，路径长度C(P)=ca1+ca2+…+cal为路径所经过的所有路段的弧长之和。最短路径问题就是求解有向图中任意给定两个节点α，z的最短路径M in(C(P)α，z)。在实际交通诱导系统中，根据诱导服务的目的不同，路段权值ca描述的因素有所区别，最短路径问题可以分为距离最短、时间最短、拥挤程度最低、道路质量最优等，本文的研究是基于行车距离最短这一条件下，符合路网较畅通条件下的交通出行目的。

2.3 经典Dijkstra算法和A*算法

Dijkstra算法求解最短路径问题的经典算法，是许多应用中解决最短路径问题的理论基础。Dijkstra算法是一个按路径长度递增的次序产生最短路径的穷举算法，求解结果是原点到其他所有各节点的最短路径，搜索空间是以原节点为圆心的圆（图1），算法比较简单，容易实现，适合小范围的最短路径的计算。Dijkstra算法是已经被证明能得出最短路径的最优解，但它的效率是个很大的问题，对于具有n个节点道路网，Dijkstra算法的时间复杂度为O(n2)，一座大中型城市的路网节点数据就能达到几万个到几十万个，Dijkstra算法并不太适合在大型交通网络中使用。而启发式A*算法的基本思想是引入启发函数h(n)优先搜索最佳邻接路段节点，节点n的估价函数定义为f(n)=g(n)+h(n)，式中g(n)是开始节点到节点n的最小代价路径的代价，h(n)是节点n到目标节点之间代价的估计，称为启发函数，f(n)就代表节点n总的代价。

图1 Dijkstra算法的搜索空间

2.4 双向启发式A*算法

双向搜索就是将搜索过程分解成独立的两个搜索过程同时进行，即从原结点到目标节点正向搜索过程和从目标结点向原节点的逆向搜索过程，其关键在于终止条件和切换条件的设定。双向启发式A*算法[2]结合双向搜索技术和启发式信息提出的一种快速搜索算法，它由正向启发式A*算法和逆向启发A*算法叠加进行。正向过程启发算法的启发函数基于目标节点计算，而逆向过程启发式函数则基于原节点计算，本文计算均采用曼哈顿（M anhattan）距离：

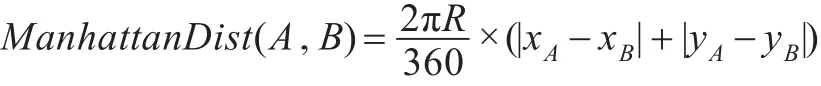
其中(xA，yA)为节点A的经纬度，(xB，yB)为节点B的经纬度，R为地球的半径，常量。

理想状况下，正向搜索和逆向搜索在原节点和目标节点的几何中心相遇，这样可以减少50%的搜索空间，搜索空间如图2。但在实际路网中，原节点和目标节点所处的路网密度、通达程度等均不同，搜索很可能不在中间点相遇，在极端情况下，甚至可能导致双向启发算法的搜索节点为单向启发搜索的两倍。因此，设计一个好的双向启发式搜索算法的关键是使其在搜索区域的中间部分相遇，而避免算法在中间部分不相遇，本文采用“迭代式最佳节点替换法”实现前向启发式搜索和后向启发式搜索切换来满足中间部分相遇和退出条件的要求。

图2 双向启发式A*算法搜索空间

具体的改进方法是不使前向和后向搜索进行简单的交替切换执行，具体步骤如下：

（1）进行前向搜索，生成一个前向最佳节点。

（2）后向搜索以此前向最佳节点为目标节点，同时生成一个后向最佳节点，当执行前向搜索时以此后向最佳节点为目标节点。

（3）反复迭代，直至相遇退出。

前向和后向之间的切换取决于搜索空间最佳节点的启发式估价函数，如果在前向搜索中基于目标节点的当前节点的估价函数小于后向搜索基于原节点的当前节点的估价函数，这就意味着在前向搜索中更偏于“中间区域”，此时执行后向搜索，反之，则执行后向搜索，这样就能保证前向和后向搜索中间区域相遇的理想情况。

3 结果对比分析

为了验证搜索算法的有效性，在W indow s操作系统平台下基于.net技术和Visual Studio工具开发出路径诱导原型系统，分别按经典Dijkstra算法、双向启发式A*算法搜索最优路径。选取成都市真实交通网数据：39 446个节点和28 067条路段。仿真程序的运行环境为W indow s server 2008R2，Intel 2.8 GHz四核处理器，4 GB主存，512 GB硬盘。测试分为两部分：（1）测试算法的计算效率；（2）测试路径诱导结果的合理性。

3.1 算法计算效率对比

在成都市路网上随机选取10个起点和终点对（OD对），分别利用Dijkstra算法和双向启发式A*算法进行最优路径诱导，利用CPU时间来衡量算法的效率。为消除和减少误差，对每组OD对分别计算10次，并取其平均值作为诱导时间，结果如表1所示。

表1 成都市区内随机10组OD对诱导时间s

从表1可以看出，随着OD对距离的波动，搜索时间呈现相同趋势的波动。对于同一OD对，双向启发式搜索算法的平均计算时间明显小于Dijkstra算法的平均计算时间，且不同的OD之间提高幅度有所区别，平均提高78%左右，如图3所示。

3.2 算法诱导结果对比

首先对比路网上10组OD对两种不同算法之间的诱导路径结果，如图4所示，可以看出双向启发式A*算法规划出来的路径长度比Dijkstra算法规划的路径长度稍长，吻合程度很高，说明双向启发式诱导算法计算出的路线是较好的“次优路”。

图3 Dijkstra算法和双向A*算法效率对比

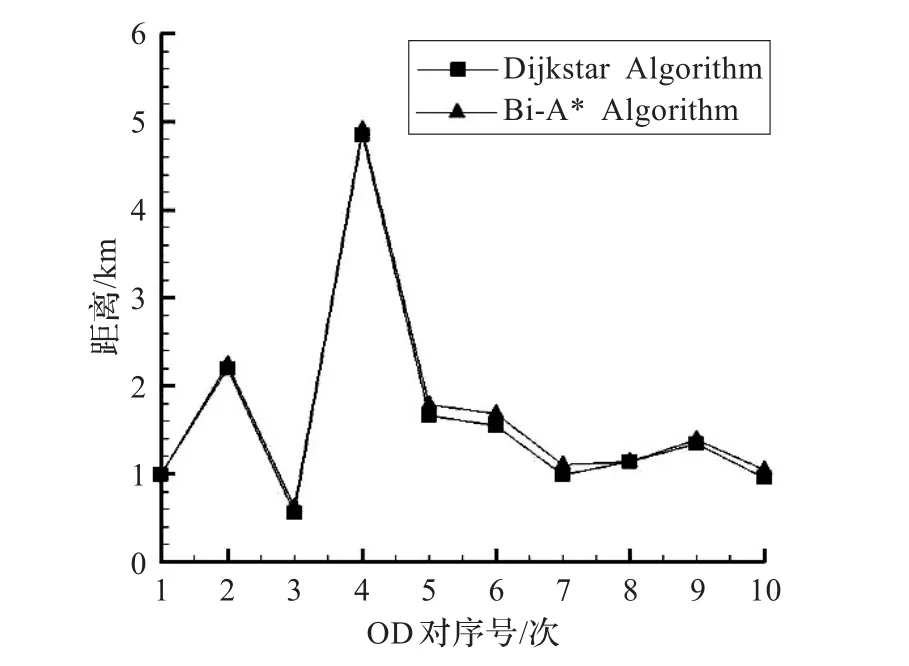
图4 Dijkstra算法和双向A*算法结果对比

其次，为了进一步量化诱导路径精度，随机选取1 000组OD点，分别使用经典Dijkstra算法和双向A*算法进行最优路径诱导，对每组OD对分别计算10次，并取其平均值作为OD对诱导时间。以Dijkstra最短距离为最优路径诱导基准，结果如表2所示，其中平均值是指算法下所有1 000组OD结果的数值平均。可以看出对于最短距离OD对，两种算法获取的诱导路径结果完全一致，而对于最长距离33 km的OD对诱导，产生3.8 km的偏差。平均而言，采用双向启发式A*算法产生4.98%的误差，基本能满足出行者的出行要求。

表2 成都市区内随机1 000组OD点结果对比

最后，对某一组OD对示例分析，起点为天一广场停车场，终点为金福路，Dijkstra诱导路径9.2 km，诱导时间0.18 s，双向启发式A*算法诱导路径9.5 km，诱导时间为0.05 s。比较而言，诱导时间有比较大的提升，而在诱导结果上，绝大部分路段重合，只有在三环路苏坡立交桥处理上两种算法结果不一致：Dijkstra算法选择从桥上通过，而双向A*算法选择从桥下箍道通过，如图5。

图5 Dijkstra算法和双向A*算法诱导路径

4 结束语

结合经典Dijkstra算法和双向启发式A*算法搜索可以发现，双向启发式A*算法在运行时间上具有明显优势，虽然规划出来的路径不是最优路径，但“次优路径”能较好地满足出行者的出行要求，具有一定的实用价值。实际中，由于司机主观偏好及路网信息认可程度等因素的影响，本文算法对研究“多准最优路径”问题提供新的研究思路。

[1]张起善.智能车辆定位导航系统及应用[M].北京：科学出版社，2002.

[2]Fu L，Sun D，Rilett L R.Heuristic shortest path algorithms for transportation applications：state of the art[J].Computers &Operations Research，2006，33（1）：3324-3343.

[3]杨瑜君.GIS中最短路径问题的研究与实现[D].成都：四川大学，2006.

[4]刘张雷，史忠科.一种基于路网变化的动态路径规划策略[J].交通运输系统工程与信息，2010，10（3）：147-152.

[5]张玲，高淑萍.动态多路选择的混合演化算法[J].计算机工程与应用，2009，45（8）：200-203.

[6]王士同.双向启发式图搜索算法BFFRA*[J].电子学报，1990，18（6）：34-39.

[7]郑年波，李清权.基于转向限制和延误的双向启发式最短路径算法[J].武汉大学学报：信息科学版，2006，31（3）：256-259.

[8]孙小荣，徐爱功，刘玉华.车辆导航中一种改进的路径优化算法[J].辽宁工程技术大学学报，2005，24（Suppl）：74-76.

YANG Yong,HU Zuo’an,HE Jinhai

School of Traffic&Transport,Southwest Jiaotong University,Chengdu 610031,China

Computational efficiency is widely recognized to be an essential issue in the optimal route planning against realistic urban road traffic network,the fast search technology is studied and a bidirectional heuristic A*algorithm is presented.Based on analysis of classic Dijkstra algorithm and heuristic A*algorithm,bidirectional heuristic A*is used to decompose the search space and binary heap data structure is utilized to operate data.Simulation results against real data demonstrate performance boost.

optimal route planning;bi-directional heuristic A*algorithm;traffic network;binary heap

A

TP18

10.3778/j.issn.1002-8331.1209-0081

YANG Yong,HU Zuo’an,HE Jinhai.Research of bidirectional heuristic A*algorithm in route guide system.Computer Engineering and Applications,2014,50（16）：54-56.

国家自然科学基金（No.61104175）。

杨泳（1982—），男，博士研究生，主要研究领域为城市智能交通、城市交通规划与管理；户佐安（1979—），男，博士，讲师，研究方向为智能铁路车流组织、智能交通；何金海（1988—），男，硕士研究生，研究方向为物流量分配及一体化研究。E-mail：yangyong@my.sw jtu.edu.cn

2012-09-12

2012-11-02

1002-8331（2014）16-0054-03

CNKI网络优先出版：2012-12-18,http://www.cnki.net/kcms/detail/11.2127.TP.20121218.1520.009.htm l