基于宏与全局变量Floyd并行算法的性能对比

李超燕，裴林滔

1.宁波职业技术学院电子信息工程系，浙江宁波 315800

2.国防科技大学计算机学院，长沙 410000

基于宏与全局变量Floyd并行算法的性能对比

李超燕1，裴林滔2

1.宁波职业技术学院电子信息工程系，浙江宁波 315800

2.国防科技大学计算机学院，长沙 410000

在Ubuntu操作系统上，实现多线程并行的Floyd算法。对实验数据分析表明，基于全局变量定义代价矩阵A大小的并行程序所获得的并行性能要优于基于宏参数定义矩阵A大小的并行程序的性能。这与相应的用宏参数定义矩阵A大小的串行程序性能要更优的结果相反。

宏参数；全局变量；Floyd算法；多线程

1 概述

Floyd算法在消防站选择，火灾消防救援，公交路线优化，物流运输路径选择，矢量地图最短路径搜索等领域中都有应用，对Floyd算法进行学习和研究是有实用价值的。在Ubuntu操作系统上对Floyd算法进行并行实现时，程序中对矩阵大小基于宏参数与全局变量的不同定义出现了并行程序所获得的性能与串行程序所获得的性能相反的结果。

在本文实验中，Floyd算法的串行程序1中的矩阵A用宏定义的参数n（n为实验数据的节点数）来定义二维数组大小：A[n][n]；Floyd算法的串行程序2中的矩阵A用全局变量nodenum（nodenum所赋的值也为实验数据的节点数）来定义二维数组大小：A[nodenum][nodenum]，其他代码与串行程序1完全相同；实验显示串行程序1的性能要优于串行程序2的性能。对串行程序1和串行程序2实现并行化后分别得并行程序1和并行程序2，并行程序1和并行程序2所用的并行指导语句完全相同，在双核的双线程下运行出现了并行程序2的性能反而优于并行程序1的结果。

2 算法原理

对于一个各边权值都不小于1的有向图，求解每对节点间的最短路径长度和最短路径可以以每个节点为源点，循环求出每对节点间的最短路径长度和最短路径，当然，Floyd算法也可求解任意两节点之间的最短路径长度和最短路径。Floyd算法又被称为传递闭包方法，串行算法的时间复杂度为O(n3)，其基本思想是递推产生一个矩阵序列A(0)，A(1)…A(k)…A(n)，其中A(0)为给定的代价矩阵，A(k)[i][j]表示从节点i到节点j之间节点序号不大于k的最短路径长度[1]。

Floyd串行算法的描述如下：

输入：有限带权图的节点数n，图的邻接矩阵Edge[n][n]，＜vi，vj＞是Edge中从节点i到节点j的弧，Edge[i][j]是弧＜vi，vj＞(1≤i，j≤N)的非负权值，权值表示从节点i到j的距离[2]；为了表示求得的任意两个节点间的最短途径，路径矩阵Path对最短路径途经的节点作记录。求A(k)[i][j]时，path[i][j]存放从节点i到节点j的中间节点编号不大于k的最短路径上前一个节点的编号。在算法结束时，由path的值追溯得到节点i到j的最短路径。Floyd串行算法[3]：

在并行算法的设计中，问题的分解通常有域分解和功能分解两种。域分解将问题分解为若干个子问题，然后分别对其并行求解；功能分解，将问题按功能分解为若干个子问题，然后分别对其求解。对于Floyd算法，选择域分解更为合适[4]。

3 算法实现

为了方便起见，约定线程数为p，节点数规模为n[5]。

for（k=0；k＜n；k++）循环开始，进行线程并行。各个任务执行并行计算：

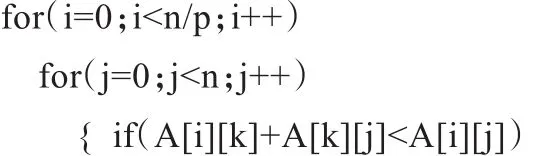
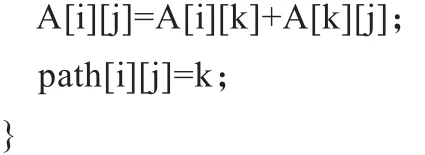
本文并行程序的设计很简单，主要是在k循环内层加并行指导命令，进行线程并行，对最短路径进行并行计算[6]。在实验中，串行程序1和并行程序1中矩阵A的维数用宏定义的n来定义大小：intA[n][n]。串行程序2和并行程序2中矩阵A的维数用全局变量nodenum来定义大小：intA[nodenum][nodenum]。串行程序1和串行程序2的其他的代码完全相同，并行程序1和并行程序2的其他代码也完全相同。

4 实验测试与分析

4.1 实验环境及实验数据

实验环境为：

（1）Intel Pentium双核T3400 CPU@2.16 GHz，2 GB内存，操作系统为Ubuntu 11.10，由gcc+openmp3.0编译[7]。

（2）Intel®CoreTMi5-2430M CPU@2.40 GHz，3 GB内存，操作系统为Ubuntu12.04，由gcc+openm p3.0编译。

（3）百万亿次巨型机，单计算节点为2路6核Intel Westmere EP6处理器，银河麒麟Linux操作系统，gcc+ openmp3.0编译。

实验数据为：节点数分别为n=100，200，…，1 000，权值范围限定不大于100，边数为n×n的10个*.txt文档。

为了验证实验的结果，本实验在三个环境下进行，用来验证实验结果的可靠性[8]。

4.2 实验结果

串行程序1，2和并行程序1，2在（1）Intel Pentium双核T3400@2.16 GHz CPU，2 GB内存，操作系统为Ubuntu 11.10的环境下编译，其中并行程序1，2以双线程运行，运行时间如表1所示（单位：s）。

串行程序1，2和并行程序1，2在（2）Intel®CoreTMi5-2430M CPU@2.40 GHz 2.40 GHz，3 GB内存，操作系统为Ubuntu12.04的环境下编译运行，其中并行程序1，2以双线程运行，运行时间如表2所示（单位：s）。

表1 在Intel Pentium双核T3400@2.16 GHz CPU，2 GB内存下运行的时间表s

表2 在Intel®CoreTMi5-2430M CPU@2.40 GHz，3 GB内存下运行的时间表s

串行程序1，2和并行程序1，2在（3）百万亿次巨型机，单计算节点为2路6核Intel Westmere EP6处理器，银河麒麟Linux操作系统，gcc+openmp3.0的环境下编译运行，其中并行程序1，2以多线程运行，运行时间如表3至表5所示（单位：s）。

表3 串行程序1，2运行时间表s

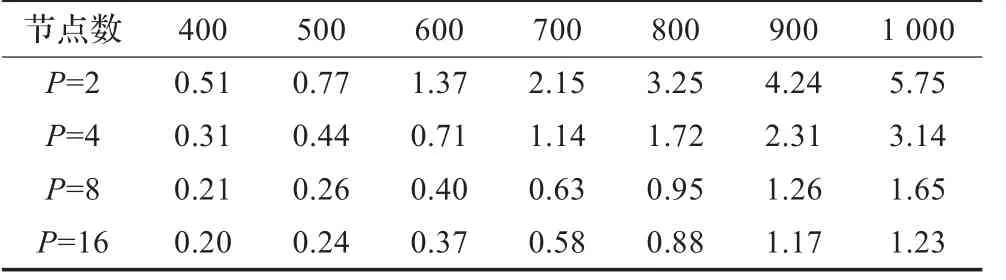
表4 并行程序1运行时间表s

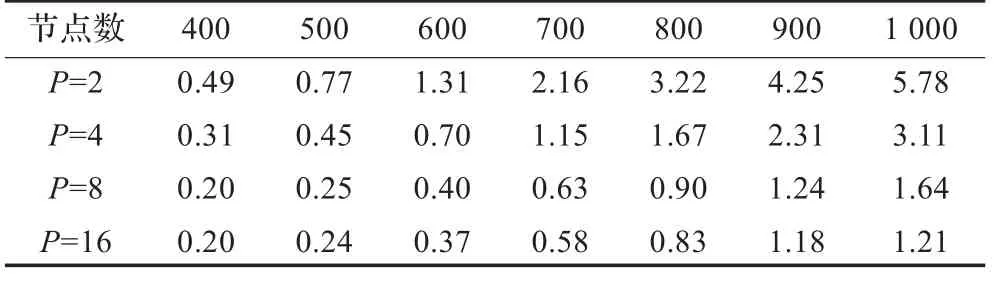
表5 并行程序2运行时间表s

本文实验数据表明：在Ubuntu操作系统下，串行程序1除了n=200，400，800外，其余的性能优于串行程序2；而并行程序2的性能都优于并行程序1。在银河麒麟Linux操作系统下，串行程序1的性能都优于串行程序2；而并行程序1的性能与并行程序2的性能相当。对于Floyd算法，在串行程序中虽然宏参数带来了性能优势，但在并行程序中反而不如全局变量。

5 结束语

Floyd算法在Ubuntu操作系统下基于全局变量所定义的代价矩阵A大小的串行程序性能虽然不如基于宏参数所定义代价矩阵A大小的串行程序性能，但前者实现并行化后其性能反而优于后者程序并行化的性能，程序加速比前者大于后者。在巨型机的银河麒麟Linux操作系统下，基于全局变量所定义代价矩阵A大小的串行程序性能同样不如基于宏参数所定义的代价矩阵A大小的串行程序性能，但前者实现并行化后其性能几乎与后者程序并行化的性能等同，加速比也是前者大于后者。对于Floyd的并行程序，宏参数并不能给程序带来性能的改善，这与串行程序的情况相反。

[1]吴向君，任凯.交互网络上任意节点对的最短路径集解法[J].海军工程大学学报，2011（4）.

[2]叶金平，朱征宇，王丽娜，等.智能交通中的高效多准最短路径混合算法[J].计算机应用研究，2011（9）.

[3]李春葆，尹为民，李蓉蓉，等.数据结构教程[M].3版.北京：清华大学出版社，2009.

[4]单莹，吴建平，王正华.基于SMP集群的多层次并行编程模型与并行优化技术[J].计算机应用研究，2006（10）.

[5]杨庆芳，刘冬，杨兆升.基于MPI+OpenMP混合编程模型的城市路网最短路径并行算法[J].吉林大学学报，2011（6）.

[6]Mocean L，Ciaca M.About parallel programm ing：paradigms，parallel execution and collaborative systems[J].Informatica Econom ică，2009，13（2）.

[7]张平，李清宝，赵荣彩.OpenMP并行程序的编译器优化[J].计算机工程，2006（24）.

[8]濮芳琍，卢炎生.一种并行程序可靠组合测试策略[J].华中科技大学学报，2009（6）.

LI Chaoyan1,PEI Lintao2

1.Department of Information Technology,Ningbo Professional Technology Institute,Ningbo,Zhejiang 315800,China
2.National University of Defense Technology,Changsha 410000,China

A multi-thread parallel Floyd algorithm is achieved on the Ubuntu operating system.Analysis of experimental data show s that the parallel performance of the parallel program with matrixAwhose size is defined with global variable is better than the parallel program with matrixAwhose size is defined with macro parameter.This is contrary to the much better performance of the serial program with matrixAwhose size is defined with global variable.

macro parameter;global variable;Floyd algorithm;multi-thread

A

TP301.6

10.3778/j.issn.1002-8331.1209-0045

LI Chaoyan,PEI Lintao.Difference of multi-thread parallel Floyd algorithm with macro parameter and global variable.Computer Engineering and Applications,2014,50（16）：45-47.

李超燕（1978—），女，副教授，研究方向为算法设计与应用；裴林滔（1988—），男，硕士生，研究方向为并行程序与高性能计算。E-mail：190515528@qq.com

2012-09-09

2012-10-11

1002-8331（2014）16-0045-03

CNKI网络优先出版：2012-12-18,http://www.cnki.net/kcms/detail/11.2127.TP.20121218.1520.005.htm l