关于丢番图方程4-(-2)2=24
2014-07-07王义锦佟瑞洲
王义锦,佟瑞洲
30建平县高级中学,辽宁建平122400;2.朝阳师范高等专科学校,辽宁朝阳122000
王义锦1,佟瑞洲2
利用初等方法给出了丢番图方程px4-(p-2)y2=2z4当p=Q2+2为奇素数时的全部正整数解,从而拓展了Mordell等学者关于ax4+by4=cz2的结果.
丢番图方程;正整数解;两两互素
对于丢番图方程
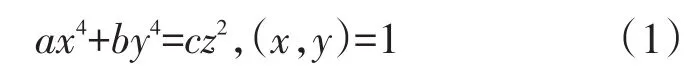
在文献[1~10]中,Mordell等学者对方程(1)进行了大量研究,本文研究了(a,b,c)=(p,-2,p-2)时方程(1)的求解问题,即研究了丢番图方程
px4-(p-2)y2=2z4,(x,y)=1,p为奇素数(2)的正整数解问题,获得了p=Q2+2(Q为奇数)时方程(2)的全部正整数解,从而拓展了Mordell等人的结果.例如p=3时方程(2)有正整数解(x,y,z)=(1,1,1),(33,1871,13),….p=11时方程(2)有正整数解(x,y,z)=(1,1,1),(241,59439,227),….
1 定理
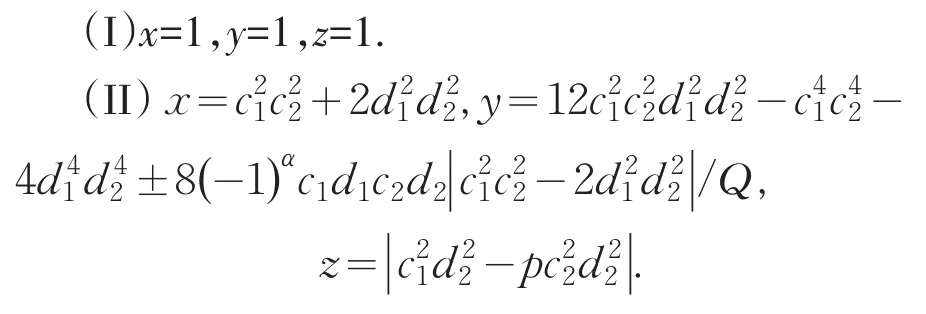

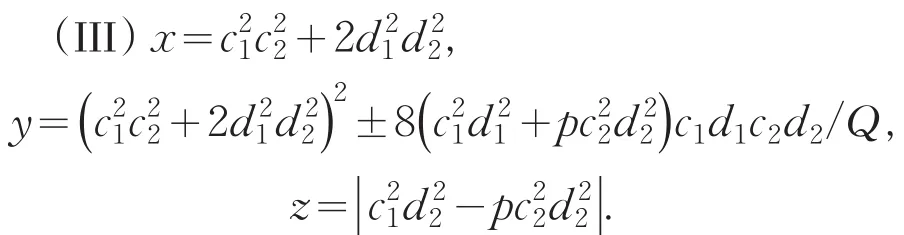
其中c2,d1满足且c1,d2满足
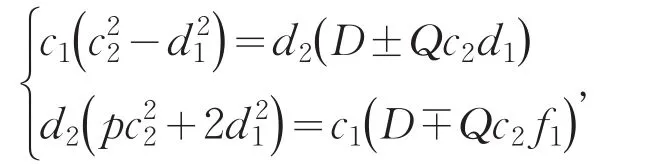
(II)、(III)中c1,c2,d1,d2两两互素且均为正整数.
2 证明
为证上述定理,先述如下引理:
引理1[11]设m无平方因数,则当m=4k±1时,丢番图方程
的所有正的本原解必可表为:
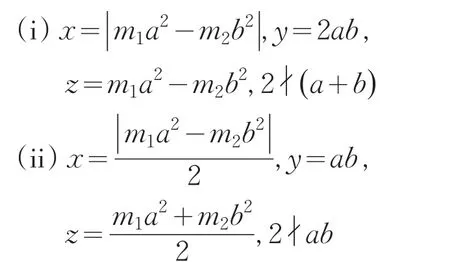
其中:a,b,m1,m2为正整数,且(a,b)=(m1,b)=(m2,a)=1,m1m2=m.
引理2[12]设0 其中:a,b,m1,m2为正整数,且(a,b)=(m1,b)=(m2,a)=1,m1m2=m. 证明因(x,y)=1,p=Q2+2由方程(2)知令,则方程(2)可化为 若l=0则1=(x,y)=(x,x2)=x,即方程(2)有解x= y=z=1. 若l>0由(3)及引理1得 或者 或者 (7)式、(8)式中的e,f满足 (i)由(6)式、(7)式中的二式有2cd=ef与2∤ef矛盾. (ii)由(6)式、(8)式中的二式有: 令c1=(c,e),c2=(c,f),d1=(d,e),d2=(d,f)则由(9)式有:c=c1c2,d=d1d2,e=c1d1,f=c2d2, c1,c2,d1,d2两两互素且均为正整数(10)把(6)中一式、(8)中二式代入(8)中三式: 此时方程(2)有解 或者 (13)式、(14)式中的e,f满足 (ii)由(12)式、(14)式中的二式知(9)式、(10)式成立。把(14)中二式、三式代入(12)中一式得: 由上式得 此时方程(2)有解 例如:在定理(II)中取d1=c1=1则D=Q,且c1,d2满足,即方程(2)有正整数解 Q为奇数.把Q=1,3代入上式,根据定理(I)不难得到下面两个例子. 例1p=3时方程(2)有正整数解(x,y,z)=(1,1,1),(33,1871,13),…. 例2p=11时方程(2)有正整数解(x,y,z)=(1,1,1),(241,59439,227),…. [1]曹珍富.丢番图方程引论[M].哈尔滨:哈尔滨工业大学出版社,1989:303. [2]佟瑞洲.关于丢番图方程x8+py2=4z4与x4+16py8=z2[J].渤海大学学报:自然科学版,2006,27(1):37-39. [3]佟瑞洲.关于丢番图方程x4+4py4=z2[J].渤海大学学报:自然科学版,2010,31(1):48-51. [4]王洪昌.关于丢番图方程x4+py4=z2[J].辽宁科技大学学报, 2009(2):113-117. [5]侯万利.关于丢番图方程x4+2py4=z2[J].辽东学院学报:自然科学版,2009,16(1):44-46. [6]王洪昌.关于丢番图方程x4+py4=z2[J].辽宁大学学报,2009, 36(2):170-172. [7]佟瑞洲.关于丢番图方程ax4+by4=cz2[J].宝鸡文理学院学报:自然科学版,2011,31(2):1-3,10. [8]熊丽华,佟瑞洲.丢番图方程ax4+by4=cz2的解法[J].辽宁大学学报:自然科学版,2011,38(4):298-302. [9]姜信君,佟瑞洲.关于丢番图方程px4-(p-1)y2=z4[J].辽宁师范大学学报:自然科学版,2012,35(2):168-173. [10]陈塞月,佟瑞洲.丢番图方程ax4+by4=cz2的一个结果[J].青海师范大学学报:自然科学版,2013,29(1):8-13. [11]佟瑞洲.广义费马方程与指数丢番图方程[M].沈阳:辽宁科学技术出版社,2011:18. [12]佟瑞洲.关于丢番图方程x2+my2=z2[J].辽宁工学院学报, 2005,25(5):349-350. 责任编辑:毕和平 Study of Diophantine Equation4-(-2)2=24 WANG Yijin1,TONG Ruizhou2 When p=Q2+2,p is odd prime,we give all positive integer solutions to the Diophantine equation px4-(p-2)y2= 2z4by the elementary methods.Thereby we expanded the result of equation ax4+by4=cz2which was studied by Mordell etc. diophantine equation;positive integer solution;prime to each other O 156.7 A 1674-4942(2014)04-0386-03 2013-07-01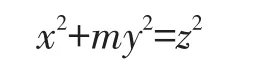
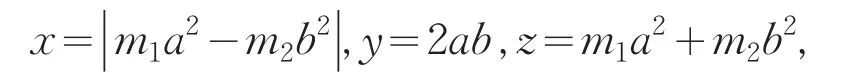
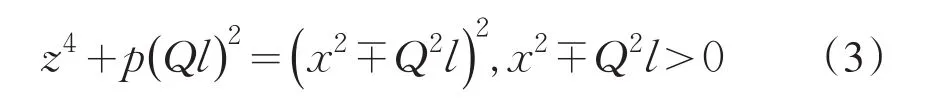
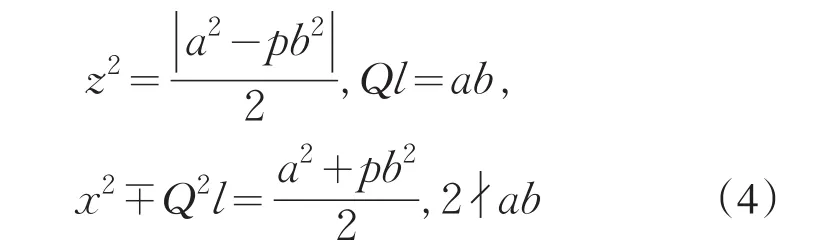
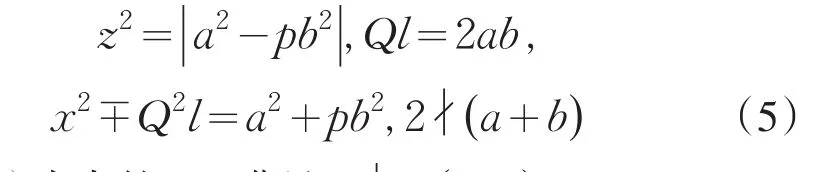
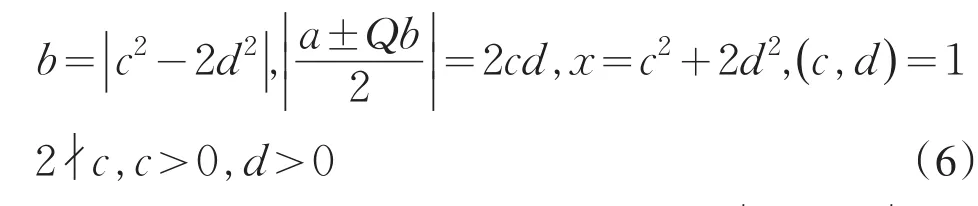
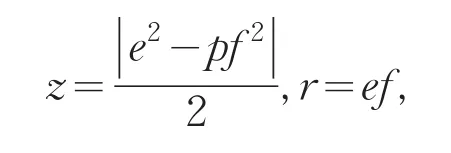
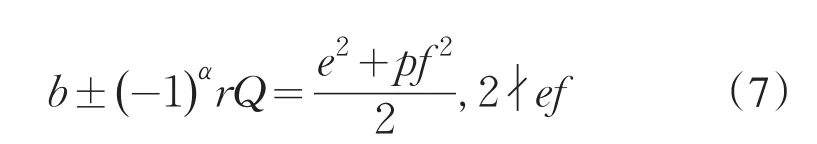
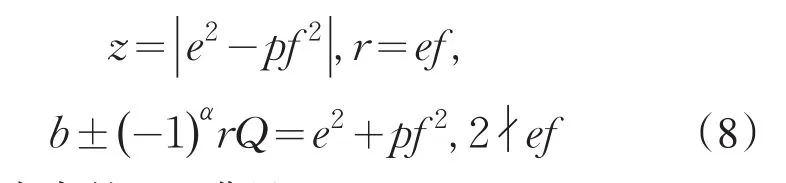
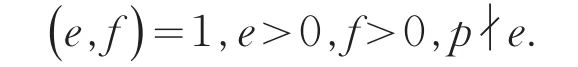

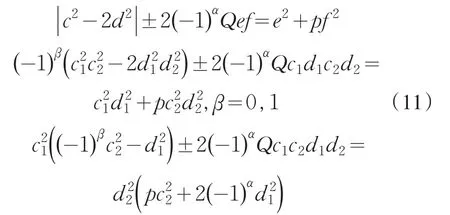
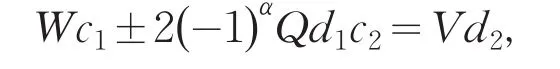
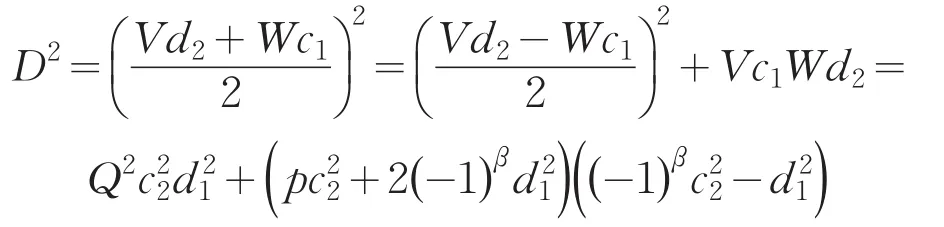
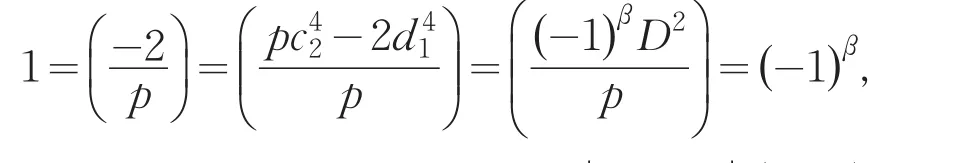
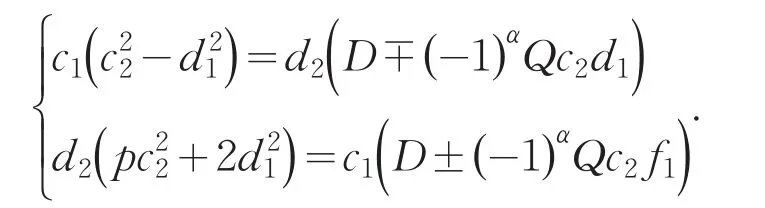
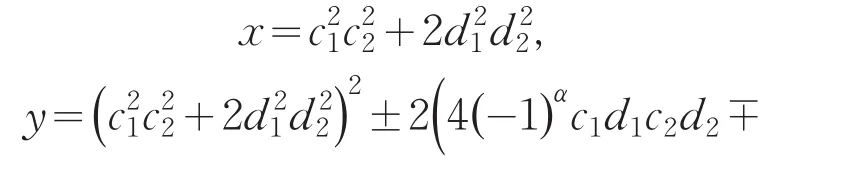
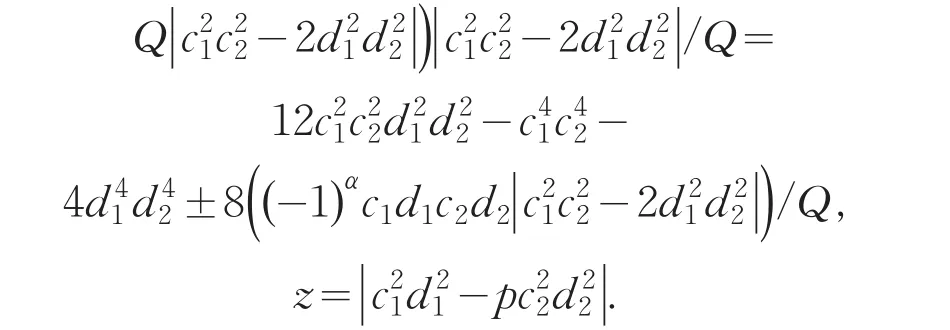
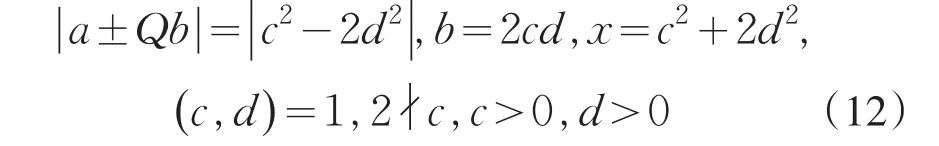
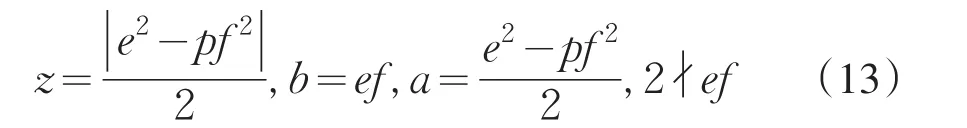
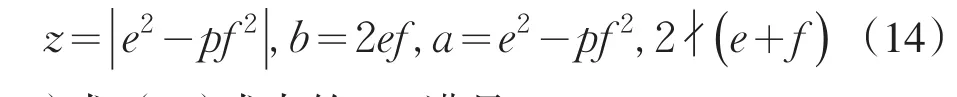
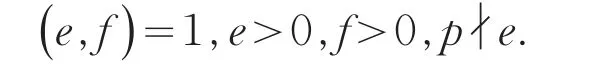
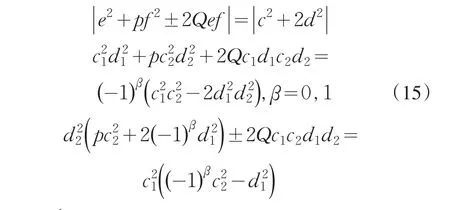
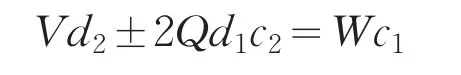
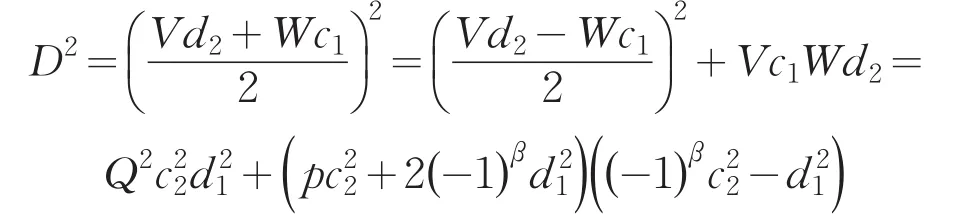
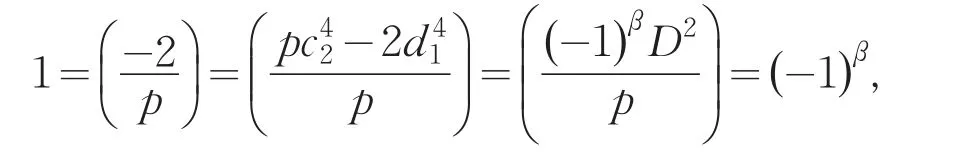
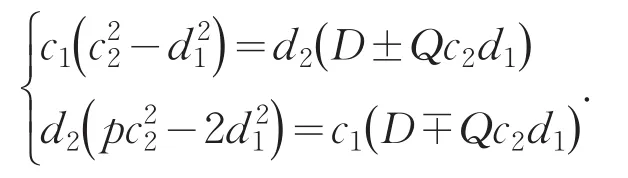
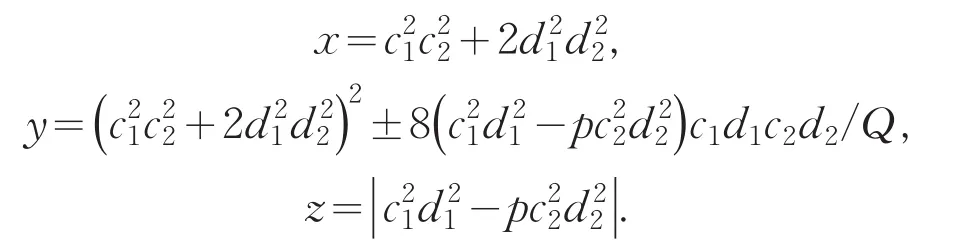
(1.Jianping Senior Middle School,Jianping 122400,China;2.Chaoyang Teachers College,Chaoyang 122000,China)
