基于国家标准的可靠性建模问题与对策探讨★

基于国家标准的可靠性建模问题与对策探讨★

刘国才1，2， 徐欣锋1， 庞红勋1， 陈春红1， 王莉莉1， 张智萌1， 李明1
（1.中国科学院空间科学与应用研究中心， 北京 100190；
2.高维信息智能感知与系统教育部重点实验室， 江苏 南京 210094）

在国家标准的约束下，针对有效载荷分系统呈现的新特点，提出了可靠性措施，并通过质量屋模型，识别出关键的可靠性措施。通过可靠性建模方法的分析，表明真值表法可以有效地实现关键可靠性措施，但存在两个难题， 分别是故障预测与系统健康管理（PHM）技术的可靠性评估和基于真值表法的可靠性分配。 给出基于真值表法的 PHM 评估方法， 并发现实现 PHM 技术的自主性是提高有效载荷可靠性的关键； 给出基于成功次数的重要度定义，并推导了可靠性建模与分配的理论公式。理论分析表明，上述方法简单、有效、易以实施并满足有效载荷分系统的工作实际。

国家标准；真值表法；故障预测与系统健康管理；有效载荷分系统

符号说明：

R*s——系统的可靠度指标；

Ni——由于第 i个分系统的成功而引起系统成功的次数；

n——分系统数；

N——系统的基本构成部件总数；

R s——系统可靠度；

ti（j）——第 i个分系统（第 j 个设备）的工作时间；

N0——试验次数；

wij——第 i个分系统（第 j个设备）的重要度，0≤wij≤1；

Rij——第 i个分系统（第 j个设备）的可靠度；

ni——第 i个分系统的基本构成部件数；

Fi——第 i个分系统的不可靠度；

rij——第 i 个分系统（第 j 个设备 ）的成功次数；

Ri——第 i个分系统的可靠度；

θi（j）——第 i个分系统（第 j个设备）的平均故障间隔时。

0 引言

国家标准是我国宇航工程中必须遵循的统一纲领，在统一标准的约束下，各承研单位生产的产品和分析结果才具备一致性、可比性和持续改进的机会。 然而至今， 我国国家标准（GB/GJB/QJ）中并无有效载荷及有效载荷分系统的通用定义。在实际工作中，航天型号研制人员和管理人员往往按照传统的理解、型号的总目标和上级的工作安排，将一部分设备规定为有效载荷或纳入有效载荷分系统管理。 关于有效载荷分系统， 该名词在文献 [1] 中规定为 “由用于进行月球科学探测的仪器设备组成的探测器分系统”。 本文中， 沿用文献 [1] 的规定，并以探月工程中有效载荷分系统为例开展有关分析工作。

1 现状分析

随着探月工程的逐渐深入和有效载荷分系统可靠性工作经验的积累，以及认识的不断提升，发现有效载荷分系统呈现如下新特点：有效载荷任务目标更高，有效载荷工作模式与时序更精细，成功判据所要涵盖的因素更多；工程总目标发生变化，工程研制队伍更年轻， “新单位” 陆续加入有效载荷分系统，可靠性学科有新的发展。这些新特点导致有效载荷分系统所采用的可靠性模型（串联/并联/串并混联/表决/冷热备）已不能更准确地满足工程需要，迫切地需要在国家标准的约束下开展深入的研究。

针对有效载荷分系统呈现的新特点，本文提出了可靠性工作措施， 通过质量功能展开[2-4]， 运用QFD 2000 分析软件建立了 “新特点-可靠性措施”的质量屋模型， 如图1所示。 在图1中， 采用定性与工程经验相结合的方法为新特点分配重要权重（0-1）， 通过 “强关联、 中关联、 弱关联” 建立新特点与可靠性措施之间的相关关系矩阵，得到可靠性措施的相对重要权重条形图（如图2 所示）。 由图2可以直观地识别出关键可靠性措施为 “提高可靠性评估准确性、考虑不同层级责任主题的关注程度、 考虑多层级多因素的任务判据”。

图1 有效载荷分系统新特点与可靠性措施的质量屋模型

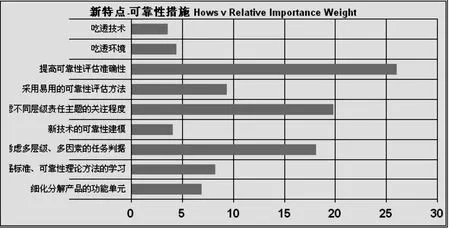
图2 可靠性措施的相对重要权重

2 建模方法分析

关键可靠性措施的有效落实是适应有效载荷分系统新特点的重要需求，而有效的可靠性建模方法是关键。 依据文献 [5]， 建立可靠性模型常用的方法有普通概率法、布尔真值表法及蒙特卡罗模拟法等。其中普通概率法是根据可靠性框图，用普通的概率关系式拟定可靠性数学模型，包括串联模型、并联模型、 冗余（贮备）模型、 表决模型、 复杂网络模型及多功能系统。布尔真值表法，考虑失效和成功两种情况，通过功能单元的状态枚举，根据独立事件概率乘法定理即可得出完成任务的可靠性值。蒙特卡洛法以计算机为工具，以概率统计为基础，进行随机变量的抽样试验。

当前，普通概率法和布尔真值表法及相关计算步骤已被明确地列入国家军用标准，而蒙特卡洛法则多见于文献研究， 例如文献 [6]。 此外， 智能方法等其他方法也被应用于可靠性建模研究，例如文献 [7-9]。 普通概率法就是当前有效载荷分系统，同时也是我国宇航工程中普遍采用的可靠性建模方法，该方法简单、易用，适用于比较简单的设备，特别是图形化的建模方法易以被广大工程人员所接受。布尔真值表法虽不具备图形化的建模特点，但达到同等效果的同时还可以充分考虑更多的因素，例如任务权重、复杂成功准则等。

例如：某型号产品由n个分系统组成，成功判据分为圆满成功、基本成功和失败。工程实践表明， 例如文献 [10]， 许多产品在不同判据下的可靠性框图模型是不一样的，从而得出每个判据下的产品可靠度值，这就会导致无法与可靠度指标值比较的问题。相反，采用真值表法评估产品的可靠度就可以解决这个问题。此外，由于真值表法可以涵盖任务权重、工作时序等复杂因素，所评估的可靠度值更准确，更接近真实情况。

总之，理论上讲，真值表法较蒙特卡洛法的运算量小，易以被工程技术人员所接受，其准确性优于普通概率法。但是，真值表法要在有效载荷分系统中得到系统的应用， 尚有两个难题需要解决： 1）PHM 技术的可靠性评估问题； 2）基于真值表法的可靠性分配。

3 PHM 技术可靠性评估

故障预测与系统健康管理[11]（PHM： Prognostics and health managenment）最早起源于美国马里兰大学 CALCE 研究中心， 已被列入 NASA、DOD 等部门的国防军工标准中。 在我国， PHM 的研究刚刚起步， 并于 2011 年和 2012 年连续召开两届 IEEE 中国大陆国际会议。 PHM 技术在我国宇航工程中的应用还步履艰难，主要原因在于：微型高精及新型传感器尚无研制能力，同时受到国外航天大国的技术封锁与禁运；故障诊断尚不成熟，故障预测更是不易。

尽管如此， PHM 的核心思想及基本技术在有效载荷分系统中一直得到广泛的应用。例如：一次电源的在线监测就可以及时地感知产品的过载、短路、断路等故障，辅助故障定位、隔离与控制。以某有效载荷为例，一次电源监测的系统设计如图3所示。单元1的功能是采集一次电源信号，经过信号调理和采样变换， 输入 CPU， 实现对电源的监测。工程实践表明，单元1的存在会使有效载荷工作得更好，即使没有也不影响有效载荷的主要功能， 所以常见的做法是单元1与单元2做串联处理，如图4所示。

针对图4， 采用真值表法进行分析， 如表 1所示。 假定单元 1 的可靠度 R1=0.9， 单元 2 的可靠度R2=0.9， 则有效载荷的可靠度为：

若采用串联模型，则有效载荷的可靠度为：

显然，真值表法能够较准确地反映可靠性真实水平。

针对式（1）做如下变换：

由式（3）可以看出， 有效载荷的可靠度完全由 R2决定， 而 R1并不影响产品的可靠性。 由此，可得出如下推论：

a）推论 1： 有效载荷的功能单元数为 n， 当状态枚举 2n次， 且每个功能单元成功次数相同且为 2（n-1）时， 有效载荷的可靠度取最大值， PHM 单元并不影响有效载荷的可靠性。

b）推论 2： 有效载荷功能单元数为 n， 当状态枚举次 2n， 且每个功能单元成功次数不相同时， 有效载荷的可靠度均小于最大值， PHM 单元会降低有效载荷的可靠性。

c）讨论： 可以采用 n 为奇数（或偶数）的举例法证明推论1与推论2的正确性。 在工程实践中， 类似一次电源检测的 PHM 设计普遍存在， 实际情况表明该设计为提高产品的测试性及故障诊断防护起到了很大的作用。然而理论分析的结果却是PHM 单元对不可修产品的可靠性无贡献， 甚至起副作用， 这表明提高 PHM 单元的自主性是提高有效载荷可靠性的关键。

图3 有效载荷示意图

图4 单元1与单元2的串联模型

表1 单元1与单元2的真值表

4 基于真值表法的可靠性分配

AGREE 分配法[12-13]是由美国电子设备可靠性顾问团提出的一种有效方法，该方法同时考虑了系统的各单元的复杂度、重要度和工作时间。然而重要度要通过统计实验或现场数据获得，这导致得到的结果缺乏客观标准。特别是在产品设计阶段，重要度数据不是十分充分，无法较客观地反映各部件在系统中的重要程度。而真值表法恰可以简单、易行地提供较客观的数据。

a）重要度

定义重要度为分系统（或设备）的成功对系统成功的影响程度， 以 wij表示重要度， 则

b）复杂度

定义复杂度为分系统的基本构成部件数在系统中的比重， 以 Ci表示复杂度， 则

c）可靠度分配

以常见的串联、 并联组成的混联模型为例（如图5所示）， 满足指数分布的前提下介绍基于真值表法获得重要度数据后的可靠度分配原理。

图5 混联框图模型

系统可靠性的数学模型为：则得到分配的平均故障间隔时间为：

5 结论

在国家标准的约束下，理论分析表明，真值表法可以很好地满足有效载载荷分系统对可靠性建模的新要求，评估较确切的可靠性水平。真值表法不仅适用于含有 PHM 技术的可靠性建模， 还进一步地发现 PHM 技术对不可修产品的可靠性贡献甚微， 提高有效载荷的自主性是推广 PHM 技术和提高可靠性的必然途径。真值表法获取的重要度数据可以较客观的用于有效载荷分系统的可靠度分配，该方法解决了重要度数据难以获取和客观一致的实际问题，分配原理进一步表明该方法简单、易行。

[1]QJ 20001-2011， 月球探测工程术语 [S].

[2] 刘国才.产品保证在航天工程中的分解 [C]//第十届全国月球科学与比较行星学陨石学与天体化学学术研讨会，2012， 187-191.

[3] 李跃生， 林树茂， 李文钊.适于大型复杂航天系统的QFD 与 FMECA 技术及应用 [M].北京： 中国宇航出版社， 2011.

[4] 李朝 玲. 质量功 能展 开的 系统建 模 及 应 用研 究 [D]. 青岛： 青岛大学， 2009.

[5]GJB 813-1990， 可靠性模型的建立和可靠性预计 [S].

[6] 苏春， 王圣金， 许映秋.基于蒙特卡洛仿真的液压系统动态可靠性 [J]. 东南大学学报， 2006， 6（3）： 370-373.

[7] 刘国才， 于强， 董晓铮， 等.可靠性设计软件的调研及其 问 题 分 析 [J]. 电 子 产 品 可 靠 性 与 环 境 试 验 ，2008， 26（4）： 19-23.

[8] 刘国才， 于强， 董晓铮， 等.MATLAB 用于空间综合材料装置的可靠性分析 [J].电子产品可靠性与环境试验，2008， 26（5）： 60-64.

[9]LIU Guocai（ 刘 国才 ）.Reliability evaluation models for high-reliability&long-life and high-reliability&short-life products[C]//IEEE 2011 9th International Conference on Reliability， Maintainability and Safety（ICRMS）， 2011.

[10] 景勤， 邵光杰， 王海燕， 等.美国航天飞机 G-435、 G-434 搭 载 桶 搭 载 方 案 研 究 [J]. 燕 山 大 学 学 报 ，2004， 28（3）： 204-209.

[11]LIU Guocai（ 刘 国 才 ）.Sliding FFT for analyzing the abrupt fault caused by SET[C]//IEEE International Conference on Prognostics and System health management（PHM-Shenzhen）， 2011.

[12] 向宇， 黄大荣， 黄丽芬.基于灰色关联理论 AGREE 方法的 BA 系统 可靠 性分 配 [J]. 计算 机应 用研 究，2010， 27（12）： 4489-4491.

[13] 邵延峰， 薛红军， 张玉刚.复杂串、 并联系统的可靠性分配方法 [J].飞机设计， 2007， 127（12）： 51-53.

新型热敏涂料可伴随温度变化来改变汽车的颜色

据报道，英国专家使用一种热敏反应涂料涂敷在尼桑 Skyline R 33 汽车的表面， 当倾倒冷水时会使汽车变色。

据称，无论什么时候将水倾倒在汽车上，车身都将变色， 这种涂料被称为 “热彩色涂料”。 英国康堤汽车公司在汽车表面一层薄漆上涂反应涂料，反应元素能够悬浮在油漆中的水或者溶剂上，根据这一原理可将微粒散布在整个物体的表面。这就意味着当温度变化时，车身颜色将从一种颜色变成另一种颜色：当温度下降时，通过涂料作用将汽车底色隐藏起来；但当温度再次升高时，涂料将使汽车变成无色。

伴随着温度变化，这种涂料将使汽车更具个性化，能够呈现不同的颜色，热彩色涂料包含的色素可以随着温度变化，从一种颜色变成另一种颜色。目前有两种类型的热彩色涂料——液晶和无色染料。

液晶涂料能够更精确地探测温度变化，但呈现色彩变化有限；无色染料具有多种颜色，但仅能显示加热或者冷却两种方式。

这种涂料并不能直接应用于汽车，它们以密封在微型胶囊的形式进行出售；然而由于汽车大量时间暴露在户外紫外光线下， 这种涂料仅能持续 4～6 个月。康堤汽车公司指出，购买紫光线添加剂可以保护汽车，延长这种热反应涂料的使用寿命。

目前该涂料的售价为 199 英镑/L， 汽车装饰店对尼桑 Skyline R 33 汽车喷漆需要 7.5 L。

（摘自腾讯科技）

Problem s about Reliability M odel Development and its Solutions Based on National Standards

LIU Guo-cai1，2， XU Xin-feng1， PANG Hong-xun1， CHEN Chun-hong1， WANG Li-li1，ZHANG Zhi-meng1， LIMing1
（1.Center for Space Science and Applied Research， Chinese Academy of Sciences， Beijing 100190， China；2.Key Laboratory of Intelligent Perception and Systems for High-Dimensional Information， Ministry of Education， Nanjing 210094， China）

In the frame of the national standards， amethod to improve the reliability of the payloads is offered based on their new features， and the key method is identified using the house of quality（HOQ）.By analyzing reliabilitymodeling， it is shown that the true table can effectively realizing the key reliability measures， but there are two difficulties， i.e.assessing reliability of PHM technology and allocating reliability index based on the true table.In this paper， the assessing method of PHM based on the true table is proposed.Based on new concept of importance， the new equation for assigning reliability offered.Theoretical analysis shows that the abovemethod was effective.

national standard； true table； PHM； payload subsystem

TB114.3

:A

:1672-5468（2014）01-0036-05

10.3969/j.issn.1672-5468.2014.01.008

★资金项目: 高维信息智能感知与系统教育部重点实验室（南京理工大学）开放基金项目资助（30920130122005）

2013-06-04

刘国才（1981-）， 男， 河北涿州人， 中国科学院空间科学与应用研究中心助理研究员， 分系统质量师， 从事控制理论与工程、智能数据处理、质量管理和可靠性、安全性的研究工作。