基于能量法和特征值法的颤振预测数值方法研究

刘一雄，刘廷毅，王德友，丛佩红，王延荣

（1.中航工业沈阳发动机设计研究所，沈阳110015；2.北京航空航天大学能源与动力工程学院，北京100191）

基于能量法和特征值法的颤振预测数值方法研究

刘一雄1，刘廷毅1，王德友1，丛佩红1，王延荣2

（1.中航工业沈阳发动机设计研究所，沈阳110015；2.北京航空航天大学能源与动力工程学院，北京100191）

为研究适用于工程设计的颤振数值预测方法，采用能量法和特征值法对出现颤振现象的真实叶片进行预测。通过将2种数值方法的预测结果与试验结果进行对比，验证数值预测方法的精度和工程适用性。结果表明：2种方法都较准确的判断了某典型风扇转子叶片的气弹稳定性，与试验结果基本吻合，具有较高的工程实用价值。

颤振预测；能量法；特征值法；非定常气动力；航空发动机

0 引言

随着设计要求的提高，航空发动机日益向高负荷、高效率、高可靠性、高推重比的方向发展。而随着推重比的提高，级压比增加，叶片变得更薄，非定常气动载荷加大，再加上新型轻质材料的应用，使得叶片刚度大幅降低，导致发动机叶片振动尤其是颤振问题更加突出。叶轮机械叶片颤振预测方法从早期基于相似理论的经验法发展到了当前的数值预测方法[1]。由于经验法过分依赖于试验数据的积累和经验的判断，不能准确预测一些新型压气机/风扇叶片。因此，发展适用于工程设计的颤振数值预测方法对发动机安全设计、缩短设计周期、节省经费等都有深远意义。叶片颤振问题的数值研究方法主要分为经典方法和耦合方法[2]。经典方法通过对气动及结构模型作一定的简化，忽略流体与结构的耦合关系，将流体与结构分开求解，其主要包括能量法和特征值法。由Carta[3]提出的能量法基于以下假设：颤振以转子振动的某一自然振型出现，通过计算这一振型与流场之间的能量平衡来预测；特征值法是以叶片的振动方程为基础，将叶片的结构动力方程与非定常气动特性结合起来，形成统一的气动弹性方程，将稳定性问题转化为特征值问题，根据特征值虚部的正、负来判断叶片是否发生颤振。

虽然能量法与特征值法求解颤振问题并不能真实描述颤振的物理本质及流固耦合关系，但是随着计算能力的提高，通过对模型的适当修改并采用合理的假设，是可以实现所谓的弱耦合[4]的，并且计算量小、计算周期短、精度较高，是比较不错的工程选择。

本文基于发展的能量法和特征值法，以某发生颤振的风扇叶片为对象，采用数值模拟的方法研究了叶片颤振的机理。

1 数值方法和求解技术

1.1 能量法

能量法是从能量交换的角度来考察叶片是否颤振，在叶片的1个振动周期内，叶片振动系统从外界获得的能量与系统阻尼消耗的能量的正负决定了叶片是否颤振。叶轮机械结构的机械阻尼远小于气动阻尼[5]，因此，叶片振动系统从外界获得的能量主要是气动力作功，通过判断非定常气动力在1个周期内对叶片作功的正负来判定是否发生颤振。

叶片在单位面积上1个周期内的气动功为

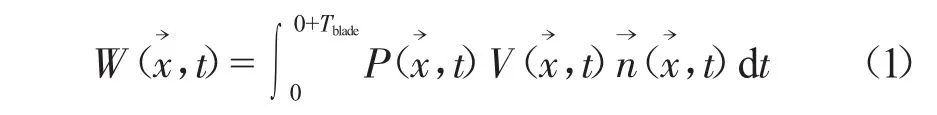
阻尼的作用就是消耗能量，在振动分析中经常采用能量方法将复杂的、非线性的阻尼模型简化为线性黏性阻尼[6]。对于气动阻尼，当流场绕流情况较好，没有强的非线性如漩涡等特征时，可以用等效黏性阻尼来近似表示气动阻尼，等效的原则是：非定常气动功在1个周期内对叶片作功等于气动阻尼在1个周期内消耗的能量。

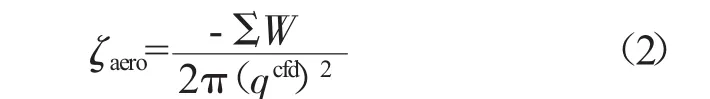
式中为各方向气动功的叠加；qcfd为正则坐标系下的模态振幅。

在进行非定常计算时，固体网格比流体网格稀疏很多，通过将固体节点上的位移插值到流体节点上实现数据交换[7]。由于叶片的振动会引起流场变化，且对全部流场进行网格点更新会浪费大量时间，因此,为了反映叶片振动对流场的作用同时为了保证效率，Slone[8]等考虑将流体域分为固定域和可动域，这样只需要实时更新可动域的网格就可以较好地模拟流场与固体交互影响的振荡过程。

非定常计算完成后，通过计算1个周期内的气动功及等效模态气动阻尼比，作为判定颤振是否发作的依据。若W＜0，ζ＞0则气动力作功为负，系统稳定；反之则系统不稳定。

1.2 特征值法

采用影响系数法[9]建立整环叶栅模型，假设叶栅在某一阶模态振荡作用下，只有1片叶片振动，其它叶片不动，通过非定常计算得到叶栅所有叶片与参考叶片运动相关的非定常气动力。

式中：Pn为第n个节径的非定常气动力；an为n节径对应的气动力影响系数；Qn为n节径对应的复数振幅。在不同叶片间相位角下，通过对Pn的叠加可以得到叶片的非定常气动力。

将物理坐标系下的振动方程变换到模态坐标系下，并进一步变换到行波坐标系下，可以得到

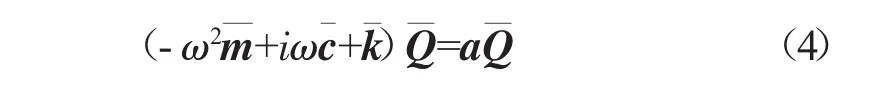
将式（5）代入式（4)可以得到

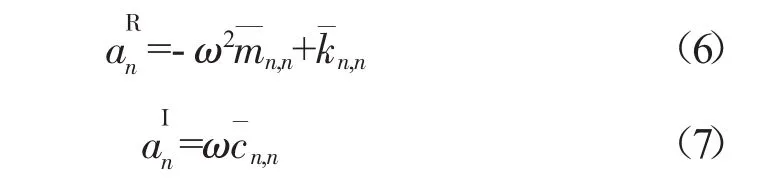
从式（6）和（7)可知，特征值的实部对应振动方程的刚度，虚部对应振动方程的阻尼。因此，虚部为正时，非定常气动力对系统起到稳定作用；虚部为负时，则非定常气动力对系统起到激励作用，系统不稳定。

2 计算结果及分析

某风扇转子叶片发生了典型的颤振现象，以该叶片为模型，给定80%转速近喘点附近的工况，基于能量法和特征值法，研究了叶片在1阶弯曲模态振荡作用下的气动弹性稳定性，并与试验结果进行对比验证。

2.1 能量法计算结果及分析

采用8节点6面体单元，在80%转速下，建立有限元模型如图1所示，通过模态分析得到了该叶片1阶弯曲模态的振型及其动频，如图2所示。

由于叶片间相位角对气动弹性稳定性的影响较大[10]，因此,建立了整环叶栅模型（如图3所示）。给定节径数为n，整环叶片数N，则各相邻叶片间相位角

图1 有限元模型

图21 阶弯曲模态（289 Hz）

图3 整环叶栅流场模型

为了加快非定常计算的收敛速度，首先，进行定常分析，并以此作为非定常的初始条件。然后计算在1阶弯曲模态振荡作用下非定常气动力对整环叶片的所做气动功和振荡稳定后的模态气动阻尼比，模态气动阻尼比随节径的变化规律如图4所示。

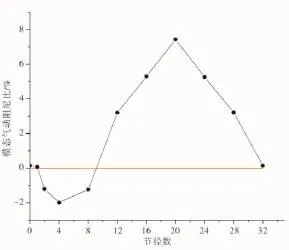
图4 模态气动阻尼比随节径变化规律

从图4中可见，模态气动阻尼比随节径数增加呈现正弦变化规律，且在2～8节径处，非定常气动力对叶片作功为正，模态气动阻尼比为负，叶片吸收能量，系统不稳定，这与试验中叶片发生颤振的现象一致。2.2 特征值法计算结果及分析

特征值法定常计算采用能量法的结果，并以此作为非定常的初始条件。进行非定常计算分析时，假定参考叶片以1阶弯曲模态振动，其他叶片不动，进行非定常计算分析。待振荡稳定后，提取物理坐标系下各叶片表面的非定常气动力及其振动位移，并将之转换到模态坐标系下，得到各叶片的非定常气动力影响系数的幅值分布，如图5所示。从图5中可见，参考叶片的振动对其自身的影响最大，对其相邻2个叶片的振动影响次之，对其它叶片的影响较小，基本可以忽略。因此，气动力影响系数矩阵采用5对角矩阵即可满足计算精度[11]。

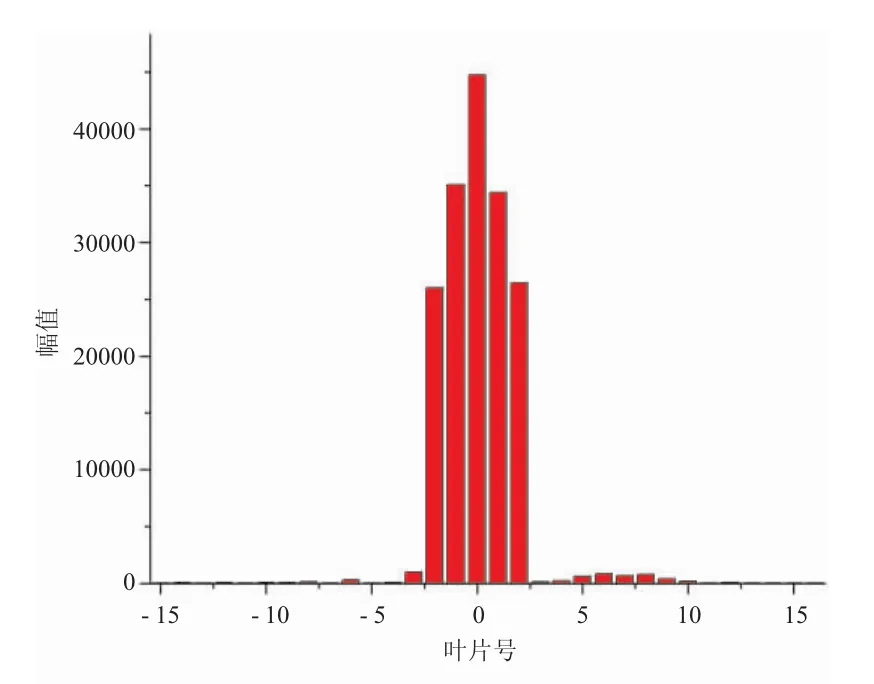
图5 气动力影响系数幅值分布

基于特征值法得到复数形式的特征值，特征值在复平面的分布如图6所示。复数特征值的实部表示振动系统的频率，虚部表示振动系统的气动阻尼，虚部的正负决定了系统的气动弹性稳定性。从图6中可见，特征值的虚部有负值出现，表明系统发生了气动弹性失稳，有颤振现象发生，这与试验结果一致。

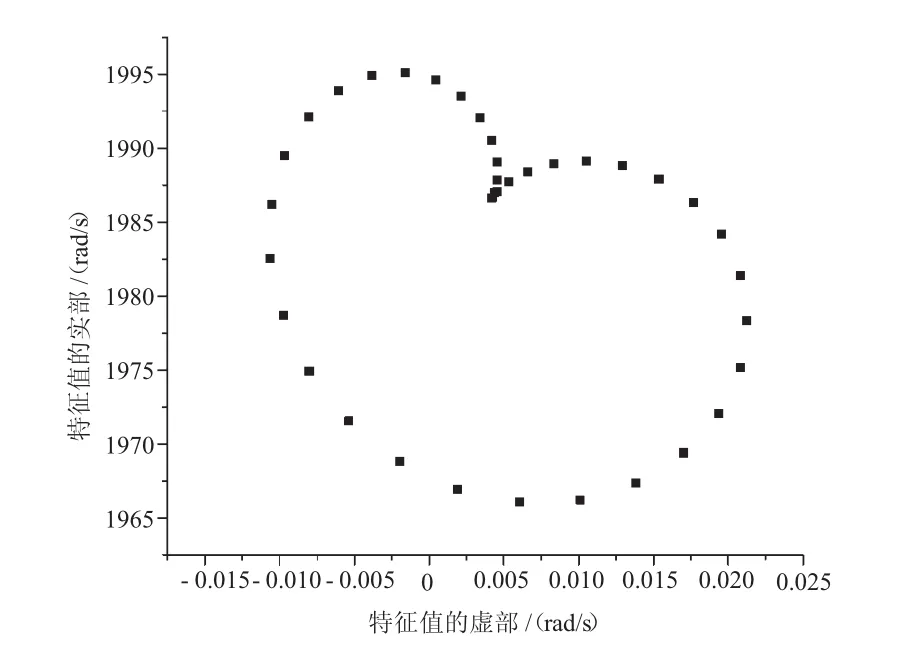
图6 特征值在复平面的分布

在行波坐标系下，得到了气动力影响系数的共轭转置矩阵，其虚部为负表示叶栅气动弹性失稳。气动力影响系数共轭转置矩阵的虚部随节径数的分布如图7所示。

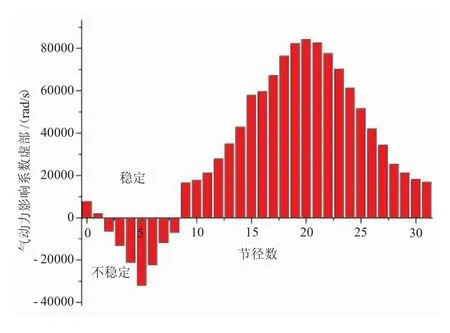
图7 行波坐标系下气动力影响系数的虚部分布

对比图4可以发现采用能量法与特征值法计算的结果相似，都在2～8节径处，判据为负，系统不稳定，发生颤振。

3 结论

基于能量法和特征值法对某发生典型颤振的风扇转子叶片进行了计算分析，结果表明：采用能量法计算得到了整环叶片在2～8节径处有正的气动功和负的模态气动阻尼比，认为叶片发生了颤振，其叶片间相位角随节径变化规律与采用特征值法求得的行波坐标系下气动力影响系数随节径数变化的规律相似。这2种方法分别从能量交换和振动方程2方面探讨了叶片颤振发作的机理，均能准确预测颤振，对叶片安全设计有指导意义，具有一定的工程实用价值。参考文献：

[1]张明明，周盛.叶轮机械叶片颤振研究的进展与评述[J].力学进展，2011，41（1）：26-38. ZHANG Mingming,ZHOU Sheng.A review of the research of blade flutter in turbomachinery[J].Advances in Machines，2011,41（1）：26-38.(in Chinese)

[2]刘文阁，冯毓诚.对经验法预测叶片颤振的分析及叶片颤振数据库的建立[J].北京航空学院学报,1986（4）:113-122. LIU Wenge,FENG Yucheng.Analysis of empirical flutter predicition method of blades and establishment of a flutter data bank[J].Journal of Beijing Institute of Aeronautics and Astronautics,1986（4）:113-122.(in Chinese)

[3]周盛.叶轮机气动弹性力学引论 [M].北京:国防工业出版社,1986：241. ZHOU Sheng.Introduction of aeroelastic in turbomachinery[M]. Beijing:National Defence Industry Press,1986:241.(in Chinese)

[4]Marshall J G,Imregum M A.Review of aeroelasticity methods with emphasis on turbomachinery applications[J].Journal of Fluids and Structure,1996,10（3）:237-267.

[5]Catra F O.Coupled blade-disk-shroud flutter instabilities in turbojet engine rotors[J].Journal of Engineering for Power, 1967,89（3）:419-426

[6]Kaza K R V,Kielb R E.Effects of mistuning on bendingtorsion flutter and response of a cascade in imcompressible flow[R]. AIAA-1981-0602.

[7]Stuart M,LI He.Blade forced response prediction for industrial gas turbines,part I:methodologies[C]//Proceeding of ASME Turbo Expo:Power for Land,Sea,and Air,2003:38640.

[8]Kielb R E,Chiang H D.Recent advancements in turbomachinery forced response analysis[R].AIAA-1992-0012.

[9]胡海岩，孙久厚，陈怀海.机械振动与冲击[M].北京:航空工业出版社，1998:285. HU Haiyan,SUN Jiuhou,CHEN Huaihai.Mechanical vibration and shock[M].Beijing:Aviation Industry Press,1998：285.(in Chinese)

[10]徐敏，陈士橹.CFD/CSD耦合计算研究[J].应用力学学报，2003，21（2）:33-36. XU Min,CHEN Shilu.Study of data exchange method for coupling computational CFD/CSD[J].Chinese Journal of Applied Mechanics,2003,21（2）:33-36.(in Chinese)

[11]Slone A K,Pericleous K,Bailey C,et al.A finite volume unstructured mesh approach to dynamic fluidstructure interaction:an assessment of the challenge of predicting the onset of flutter[J].Applied Mathematical Modelling,2004,28:211-239. [12]Hanamura Y,Tanaka H,Yamaguchi K.A simplified method to measure unsteady forces acting on the vibrating blades in cascade[J].Bulletin of the JSME,1980,23:880-887.

[13]徐可宁.叶轮机械叶盘结构气动弹性算法研究及程序实现[D].北京：北京航空航天大学,2011. XU Kening.On the algorithm of aeroelasticity and the program implementation of bladed disk assemblies in turbomachines[D].Beijing:Beihang University,2011.(in Chinese)

[14]张小伟,王延荣.叶间相位角对叶片颤振的影响[J].航空动力学报，2010，25（2）:412-416. ZHANG Xiaowei,WANG Yanrong.Influence of interblade phase angle on the flutter of rotor blades[J].Journal of Aerospace Power,2010,25（2）:412-416.(in Chinese)

[15]张小伟.叶轮机械叶片气弹稳定性数值预测方法研究[D].北京：北京航空航天大学,2011. ZHANG Xiaowei.Numerical prediction method for aeroelastic stability of blades in turbomachines[D].Beijing：Beihang University,2011.(in Chinese)

Numerical Study of Flutter Prediction Based on Energy Method and Eigenvalue Method

LIU Yi-xiong1,LIU Ting-yi1,WANG De-you1,CONG Pei-hong1,WANG Yan-rong2
（1.AVIC Shenyang Engine Design and Research Institute,Shenyang 110015,China;2.School of Jet Propulsion,Beihang University, Beijing 100083,China）

In order to study the numerical method of flutter prediction applied on the engineering design,the flutter phenomenon of a fan blade was predicted by energy method and eigenvalue method.The precision and engineering applicability of the numerical methods on flutter prediction were validated by comparing the predicted results and test results.The results show that the energy method and eigenvalue method are accuracy to diagnosis the aeroelastic stability of a fan blade,which in good agreement with the test results and are of good engineering practical value.

flutter prediction;energy method;eigenvalue method;unsteady aerodynamic forces;aeroengine

V 211.1+5

A

10.13477/j.cnki.aeroengine.2014.06.009

2013-07-06

刘一雄（1988），男，在读硕士研究生，研究方向为航空发动机结构强度振动及气动弹性稳定性；E-mail:364835973@qq.com。

刘一雄，刘廷毅，王德友，等.基于能量法和特征值法的颤振预测数值方法研究[J].航空发动机，2014,40（6）:43-46.LIUYixiong,LIUTingyi, WANGDeyou,et al.Numerical studyofflutter prediction based on energymethod and engevalue method[J].Aeroengine，2014,40（6）:43-46.