基于改进粒子群算法的航空发动机性能综合评价

赵 凯，李本威，李 冬，李海宁

（1.海军航空工程学院飞行器工程系,山东烟台264001；2.大连理工大学船舶工程学院CAD工程中心,辽宁大连116024）

基于改进粒子群算法的航空发动机性能综合评价

赵 凯1，李本威1，李 冬1，李海宁2

（1.海军航空工程学院飞行器工程系,山东烟台264001；2.大连理工大学船舶工程学院CAD工程中心,辽宁大连116024）

针对基于单参数评估发动机性能能力不足的问题，研究了利用多参数综合评估发动机性能的方法；通过对某型发动机台架试车数据分析，确定了使用综合加权法评估发动机性能比算术加权平均法更具合理性；分别利用改进的遗传算法和粒子群优化算法计算多参数的权值，对比结果表明：使用改进的粒子群算法在计算精度和速度上均优于遗传算法。同时还计算了各翻修次数下发动机的性能指标。

多参数权值；综合评判；遗传算法；粒子群算法；航空发动机

0 引言

航空发动机为飞机提供动力，其性能的优劣关系到飞机的可靠性和安全性。在发动机工作时，其性能会通过一定的参数表现出来，所以对航空发动机进行连续的性能监控是判断发动机能否稳定安全运行的有效方法。目前在航空发动机检测中多使用基于单参数测试的方法，但该方法在处理发动机这样的复杂系统时，反映问题较为单一，不能充分反映其整体性能，而且采集的数据容易受到外界干扰。而利用多参数进行发动机性能综合评估较单参数评估方法具有全面、合理和准确的特点，能够综合考虑各参数及其相互关系，从而得到更合理的评判结论[1]。因此，基于多参数发动机综合评估方面的研究越来越引起国内外学者们的重视[2]。在评估中对各参数的权值计算是目前研究的热点问题。

本文针对发动机综合评估的多参数权值寻优问题，利用遗传算法和粒子群优化算法分别进行寻优计算。目前这2种方法都在不断地丰富和完善，并越来越多地应用于航空发动机各类参数的处理和研究[3-7]。

1 理论基础

1.1 遗传算法

遗传算法 (Genetic Algorithm，GA)是由美国Michigan大学的Holland教授于1962年提出的基于模拟生物遗传和进化而形成的1种随机化搜索方法。遗传算法首先利用随机方式产生初始种群，种群中的每个个体对应着待优化问题的1个可能解。在每1代中，根据一定的适应值函数及遗传算子进行交叉和变异等操作产生出新的解集的种群，适应值高的个体被保留下来，所以新群体中各个体适应值不断提高，直至满足终止条件。最后群体中适应值最高的个体经过解码，即为待优化参数的最优解。遗传算法采用概率化的寻优方法，具有自组织、自适应和自学习性，能够在复杂空间进行全局优化搜索，并且具有较强的鲁棒性；其缺点是编程实现比较复杂、计算量较大、全局优化速度较慢，在应用中可能出现早熟现象等[4-5]。

本文利用文献[4]提出的改进的遗传算法，在经典遗传算法的基础上，加入了加速循环的过程。首先将遗传算法所产生的优秀个体的空间作为变量的初始区间，然后随着进化迭代次数的增加，逐步缩小各变量的变化区间。最后再运行遗传算法，直到满足算法终止条件。

1.2 粒子群优化算法

粒子群优化算法(particle swarm optimization，PSO)是由Kennedy[8]和Eberhart[9]博士于1995年基于对鸟群捕食行为的模拟提出的1种智能优化算法，近年来受到广泛关注。该算法能较好地解决多参数的优化问题，是1种有效的全局优化方法。在粒子群优化算法中，每个粒子具有1个适应度函数来判断粒子位置，还有1个速度值决定粒子飞行的方向和距离。最后粒子群就追随当前的最优粒子在解空间内搜索。每个粒子根据下面的公式来更新自己的速度和位置[10-12]。

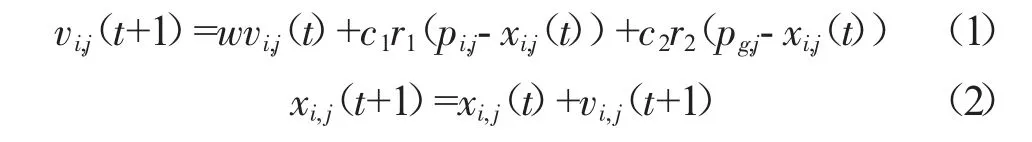
式中：i,j=1,2,…，d（d维搜索空间）；t为迭代次数；w为惯性权重；c1、c2为正的学习因子；r1、r2为0～1之间均匀分布的随机数；pi,j为粒子本身找到的最优解位置(pbest)；pg,j为整个群体找到的最优位置（gbest）。

与遗传算法相比，粒子群算法具有规则简单、计算量小、效率高、精度高、收敛快及易于编程实现等优点[12-13]。

利用粒子群算法寻优，希望算法在初期时可以快速收敛，以快速定位可能的解的大致范围，在后期时收敛速度较慢，以在小范围内仔细寻找解。调节惯性权重是比较常用的方法。当惯性权重w=1时，表明带惯性权重的粒子群算法为基本粒子群算法；当惯性权重较大时w有较好的全局收敛能力，而当w较小时则具有较强的局部收敛能力。因此，由于解的搜索范围随着算法的迭代次数的增加逐渐缩小，w应不断地减小，使得粒子群算法在初期具有较强的全局收敛能力，而后期具有较强的局部收敛能力。

文献[13]提出自适应权重，w随算法迭代的变化为

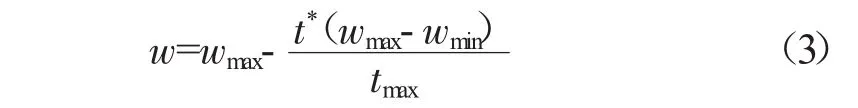
式中：wmax、wmin分别为w的最大值和最小值；t*为当前迭代步数；tmax为最大迭代步数，一般取wmax=0.9，wmin=0.4。

文献[14]采用线性降低的惯性系数，即

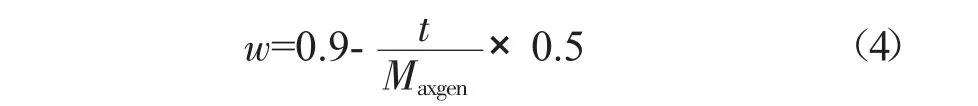
式中：t为当前迭代次数；Maxgen为最大截至迭代次数。

文献[15]通过对w函数分别取凹函数、凸函数和线性递减函数形式研究发动机模型收敛性的好坏。

定义w函数为

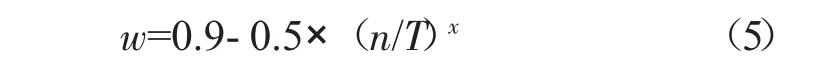
式中：T为迭代的总次数：n为当前的迭代次数：x为w函数的凹凸形态。

采用凹函数(即x＜1)时，其收敛情况相对较好；采用凸函数(即x＞1)时，由于惯性权重过大，不能收敛至目标精度；而采用线性函数时，则收敛性介于凸函数与凹函数之间。

由于本文研究的问题待优化目标的数目不多，通过计算对比发现，综合考虑计算结果及收敛速度等因素，确定了采用凹函数形式的惯性权重时，粒子群优化算法收敛的效果最好。

2 发动机性能综合评判各参数权值的确定

根据文献[1]中某型发动机500多台次经过3次翻修的台架试车数据，建立了试车数据库，并运用统计和综合分析方法对发动机性能进行了分析研究。本文选择其中部分数据作为研究对象，在文献[1]研究的基础上做进一步的综合评判方法研究。

根据对双转子发动机台架试车的分析，本文选择台架主要验收性能参数为ΔF、Δsfc、T3、T4、ΔS和全加力余气系数ALF。ΔF和Δsfc分别是推力、油耗与其对应验收曲线的上限的差值，ΔS是转差与转差验收曲线下限的差值。

为了将发动机各参数进行归一化，引入了功效函数的概念。设发动机性能矩阵为[Z]=[Z1Z2Z3…Zn]，其中，k1个性能参数希望尽量大（如F），k2个性能参数希望尽量小（如T3、T4、sfc），k3个性能参数希望尽量适中（如ΔS、ALF）。对于这些目标Zi，分别给定1个功效系数（即评分值）di（di是在（0,1）之间的某1个数）。当目标达到最满意时令di=1；当最差时令di=0。分析发动机性能验收标准可以得出di=1和di=0时的Z值，即性能Zi的上下限。通常使用验收曲线的上下边界或一定数量发动机台架性能统计的极值作为性能的上下限。描述di与Zi之间关系的函数称为功效函数。

综合加权法也称定权值综合参数算法，可以定量地计算发动机工作性能综合指数

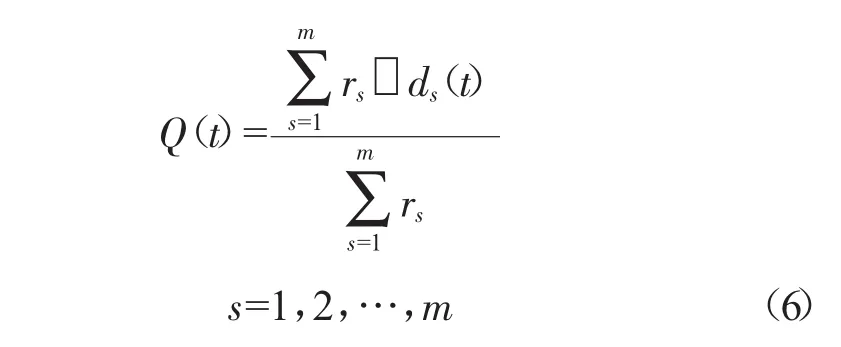
式中：m为发动机被监控参数的数目；rs为参数的权值（反映了在估计被监控状态时该参数的重要性）；ds（t）为被监测的发动机参数的功效函数值，是将发动机各参数无量纲化后的值。

不同参数的权值，一般可根据经验或寻优算法来确定。并且0≤ds（t）≤1；0≤rs≤1。

利用综合指数来表征发动机的性能，在发动机性能正常时，其综合指数值必须尽可能大，且在正常工作时的综合指数值之间离散度不应很大；在发动机性能恶化或发生故障时，其综合指数值必须尽可能小，且故障时的综合指数值之间离散度也不应很大。这样得出的综合指数才能明确地分辨出发动机的性能正常与否或正常时性能降低的速度。因此，综合参数的变化范围为：0≤Q（t）≤1。当发动机发生故障时，Q（t）=0；当发动机处于最优工作状态时，Q（t）=1。因此，通过判断Q（t）的值，可用于监控发动机的状态[3]。

文献[1]采集了发动机3次翻修的试车数据，与第1次翻修数据相比，第3次翻修后发动机性能已发生恶化，符合综合指数法的条件，可按照上述方法计算。因此，截取某型发动机在最大状态下多个参数在第1、3次翻修时对应的功效函数，见表1。

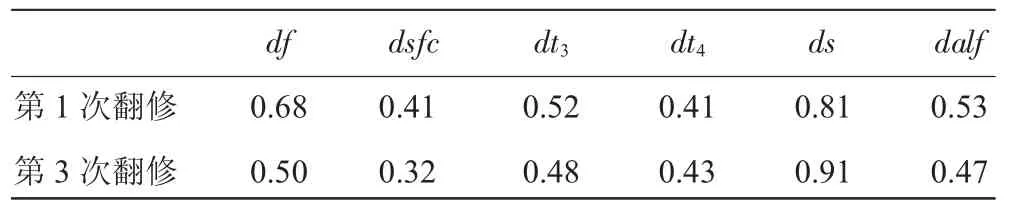
表1 发动机2次翻修时对应的功效函数

文献[1]中使用发动机各参数的功效函数的算术加权平均值来评判发动机的性能，即发动机总体性能指数

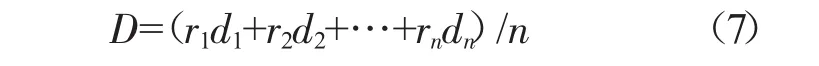
式中：r1，r2，…，rn为各种性能参数的加权系数。

实验材料东方百合‘索邦’购于北京市百合合作社。根据花被片花色积累的变化，对花蕾的9个发育时期(长度分别为5、6、7、8、9、10、11、12、13 cm)花蕾长11 cm时的11个组织部位(包括：外花被、内花被、花丝、花药、柱头、花柱、子房、上部叶、中下部叶、嫩茎和茎生根)(图1)及10种光照处理(分别为黑暗处理：1、2、4、8 h和光照处理：1、2、4、8、12、16 h)后的花蕾进行取样。样品均设置3个重复，采集后保存于 - 80℃ 冰箱备用。

利用小偏差法与发动机稳态程序计算得到各性能参数的加权系数。式（7）中显然D值越大越好。在D=1时，发动机的总体性能最佳；反之D=0时为最差。第1、3次翻修时，D1=0.55，D3=0.49。

对比式（6）和（7）可见，其区别在于分母不同。式（6）的分母为各参数权值之和，式（7）为参数数目之和。显然，当参数不同时，其对应的权值不同，权值之和也即分母也不同，所以性能指标也不同，式（6）考虑了权值的变化；而在式（7）中，参数数目确定后，分母即为定值，不会随权值的变化而改变。

2.1 基于改进的遗传算法的各参数权值的确定

选取的优化准则函数为

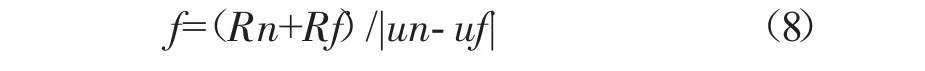
式中：un、Rn分别为在发动机正常状态时的综合指数值Q（t）的平均值和方差；uf、Rf分别为在发动机故障或性能失常时的综合指数值Q（t）的平均值和方差。

从式（8）中可见，f值越小，该权值下得到的综合指数值就越能反映发动机的性能正常与否，该权值也就越合理，因此选取f作为优化准则函数来评价所得的权值[4]。

利用改进的遗传算法计算多参数的权值，每代选取群体规模为400，优秀个体数目为40，复制概率为0.2，杂交概率为0.95，变异概率为0.6[4]。通过31步迭代计算得到各参数的权值，见表2。

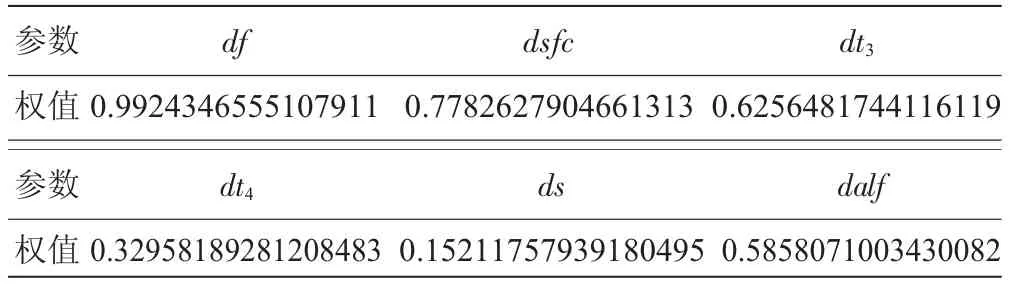
表2 基于改进的遗传算法的各参数权值

将各权值代入式（6）得：Q（t）=(0.9924346555107911× df+0.7782627904661313×dsfc+0.6256481744116119× dt3+0.32958189281208483×dt4+0.15211757939180495× ds+0.5858071003430082×dalf)/3.46385219293543228。优化准则函数f=0.025405370961755748。

2.2 基于改进的粒子群算法的各参数权值的确定

利用改进的粒子群算法计算多参数的权值，种群数为24，最大迭代次数为200，w采用凹函数递减函数形式，如图1所示。计算各参数的权值，并将之代入式（6）后得到Q（t）=（1.0000×df+0.7919×dsfc+ 0.6492×dt3+0.3237×dt4+0.1557×ds+0.6057×dalf）/ 3.5262。优化准则函数f=0.0254。

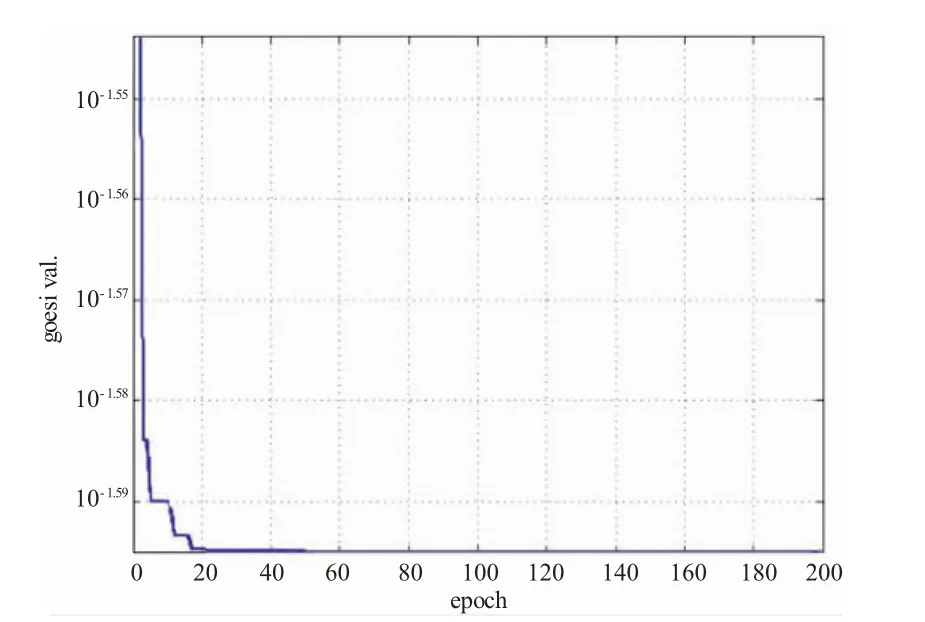
图1 利用粒子群优化算法寻优

可以看到，这2种方法的结果基本相同。但粒子群优化算法计算的结果较为稳定，运行几次后很快就收敛到定值。而且粒子群算法在编程实现、计算量、结果精度及收敛速度上要优于遗传算法。因为本文采用与文献[4]相同的遗传算法，所以使用的粒子群算法当然也优于文献[4]中所对比的专家调查法。

再利用粒子群优化算法得到的权值计算每次翻修时发动机试车数据对应的综合加权值，步骤如下：

第1次翻修时，Q（t）=（1.0000×0.68+0.7919× 0.41+0.6492×0.52+0.3237×0.41+0.1557×0.81+0.6057× 0.53）/3.5262=0.54509613748511145142079292155862≈0.5451。

第3次翻修时，Q（t）=（1.0000×0.50+0.7919× 0.32+0.6492×0.48+0.3237×0.43+0.1557×0.91+0.6057× 0.47）/3.5262=0.46241875106346775565764846009869≈0.4624。

最后再将此权值代入式（6）计算其他几次翻修时的发动机性能指标，并且对比文献[1]中使用算术加权平均法的结果，见表3。

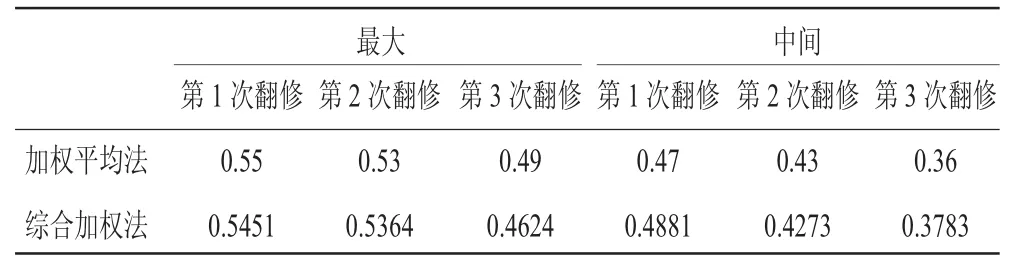
表3 使用算数加权平均法和综合加权法计算发动机翻修数据

结果表明，2种评估方法的数值在变化趋势上大体一致，但是综合加权法在计算时考虑了权值的影响，即式（6）的分母是各权值相加之和，而不是各权值数量之和，更具合理性。

3 结束语

（1）使用多参数综合评估发动机性能可以克服使用单参数方法评估所反映问题片面的缺点，具有全面、合理和准确的优点。

（2）利用遗传和粒子群算法分别求取了多个参数的权值，对比分析结果表明，改进的粒子群优化算法从算法、计算量、计算效率和编程实现等方面要优于遗传算法。

（3）综合加权法在计算时考虑了权值的影响，所以更具合理性。

（4）本文研究的多参数主要为发动机的性能参数，不能说已经对发动机的整体状态进行了评估，需要进一步融合发动机的振动及油液数据等，进行基于多源参数的航空发动机综合评估方面的研究。

[1]李珈，陶增元.某型发动机性能衰退的统计分析和预测[J].航空动力学报，1994，7（2）：173-176. LI Jia，TAO Zengyuan.Statistical analysis and prediction of aeroengine deterioration [J].Journal of Aerospace Power，1994，7（2）：173-176.(in Chinese)

[2]谭巍，李冬，樊照远,等.基于模糊信息熵的航空发动机性能评估和可靠性分析[J].航空发动机，2011，37（5）：45-48. TAN Wei，LI Dong，FAN Zhaoyuan.Aeroengine performance synthetic estimation and reliability analysis based on fuzzy information entropy[J].Aeroengine，2011，37（5）：45-48.(in Chinese)

[3]Holland J H.Adaptation in natural and artificial systems[M]. Ann Arbor:University of Michigan Press，1975：20-30.

[4]胡金海，谢寿生.基于遗传算法的航空发动机性能监控与故障诊断[J].推进技术，2003，24（3）：198-200. HU Jinhai，XIE Shousheng.Performance monitoring and faultdiagnosis of aeroengine based genetic algorithm[J].Journal of Propulsion Technology，2003，24（3）：198-200.(in Chinese)

[5]李秋红，孙健国.基于遗传算法的航空发动机状态变量模型建立方法[J].航空动力学报，2006，21（2）：427-431. LI Qiuhong，SUN Jianguo.Aeroengine state variable modeling based on the genetic algorithm[J].Journal of Aerospace Power，2006，21（2）：427-431.(in Chinese)

[6]袁春飞，姚华.基于卡尔曼滤波-遗传算法的航空发动机性能诊断[J].航空发动机，2007（S1）：104-108. YUAN Chunfei，YAO Hua.Aeroengine performance diagnosis based on calman filter-genetic algorithm[J].Aeroengine，2007 （S1）：104-108.(in Chinese)

[7]李学斌.基于多目标遗传算法的航空发动机PID控制器参数优化[J].航空发动机，2009，35（1）：23-26. LI Xuebin.Parameters optimization of PID controller for aeroengine based on multi-objective genetic algorithm[J].Aeroen gine，2009，35（1）：23-26.(in Chinese)

[8]Kennedy J，Eberhart R.Particle swarm optimization[C]//In: IEEE Int'l Conf On Neural Networks,Perth,Australia,1995：1942-1948.

[9]Eberhart R，Kennedy J.A new optimization using particle swarm theory [C]//In:Proc.of the Sixth International Symposium on Micro Machine and Human Science,Nagoya，Japan，1995：39-43.

[10]贺星，刘永葆，赵雄飞.基于进化神经网络的压气机结垢性能退化评估[J].航空发动机，2012，38（2）：41-45. HE Xing，LIU Yongbao，Zhao Xiongfei.Performance deterioration evaluation of compressor fouling based on evolving neural network[J].Aeroengine，2012，38（2）：41-45.(in Chinese)

[11]王星博，王永华，于光辉，等.引入平均最好位置的量子粒子群算法及在航空发动机非线性模型求解中的应用[J].航空发动机，2013，39（1）：23-29. WANG Xingbo，WANG Yonghua，YU Guanghui，et al.QPSO Imported average best position and application on solving nonlinear model of aeroengine[J].Aeroengine，2013，39（1）：23-29.(in Chinese)

[12]吴宏艳，张栾英.改进粒子群算法在多目标机炉协调控制中的应用[J].电力科学与工程，2011，27（10）：53-56. WU Hongyan，ZHANG Luanying.Application of one improved PSO algorithm in the boiler turbine coordinate control [J].Electric Power Science and Engineering，2011，27（10）：53-56.(in Chinese)

[13]聂瑞，章卫国，李广文，等.一种自适应混合多目标粒子群优化算法[J].西北工业大学学报，2011，29（5）：695-701. NIE Rui，ZHANG Weiguo，LI Guangwen，et al.A more useful AHMOPSO (Adaptive Hybrid Multi-objective Particle Swarm Optimization)algorithm[J].Journal of Northwestern Polytechnical University，2011，29（5）：695-701.(in Chinese)

[14]盖锋.一种速度改进型粒子群优化算法及应用 [J].现代计算机，2011，10（19）：3-6. GAI feng.A speed improved particle swarm optimization and its application[J].Modem Computer，2011，10（19）：3-6.(in Chinese)

[15]骆广琦，刘波，宋頔源.基于混合粒子群算法的航空发动机数学模型解法[J].燃气涡轮试验与研究，2011，24（2）：5-8. LUO Guangqi，LIU Bo，SONG Diyuan.Hybrid particle swarm optimization in solving aeroengine nonlinear mathematical model[J].Gas Turbine Experiment and Research，2011，24 （2）：5-8.(in Chinese)

Comprehensive Evaluation of Aeroengine Performance Based on Improved PSO

ZHAO Kai1,LI Ben-wei1,LI Dong1,LI Hai-ning2
（1.Department of Airborne Vehicle Engineering,NAAU,Yantai Shandong 264001,China;2.Institute of Marine Engineering, Dalian University of Technology,Dalian Liaoning 116024,China）

To solve the lack of ability problem for evaluate engine performance based on single parameter,the method of evaluating engine performance based on multiple parameters was studied.By analyzing the bench test data for an aeroengine,the results show that the synthetic weighted method was more rational than arithmetic weighted mean method for evaluating engine performance.Weights of multiple parameters were calculated by the improved genetic algorithm and particle swarm optimization algorithm.The comparative study shows that the improved particle swarm algorithm is superior to the improved genetic algorithm in the calculation result.Finally,the engine performance index of each overhaul was calculated.

multi-parameter weights;comprehensive evaluation;genetic algorithm;particle swarm optimization;aeroengine

V 235.13

A

10.13477/j.cnki.aeroengine.2014.06.003

2013-07-07 基金项目：国家自然科学基金（青年基金）（61102167）资助

赵凯（1983），男，在读博士研究生，主要研究方向为航空发动机评估与诊断技术；E-mail：254657425@qq.com。

赵凯，李本威，李冬，等.基于改进粒子群算法的航空发动机性能综合评价[J].航空发动机，2014，40（6）：13-17.ZHAO Kai，Li Benwei，Li Dong，et al.Comprehensive evaluation ofaeroengine performance based on improved PSO[J].Aeroengine，2014，40（6）：13-17.