模糊综合评价法在路基处理方案选择中的应用

王 淼

（唐山市交通勘察设计院有限公司，河北 唐山 063000）

0 引言

路基作为承重主体，应具有足够的强度和稳定性。坚固的路基，不仅是路面强度和稳定性的重要保证，而且能为延长路面的使用寿命创造有利条件。路基处理方案本身也是一个由众多因素组成的复杂体系，经济、技术、环境等因素都会影响方案的选择，因此对路基处理方案优选的过程，就是对系统进行综合评价的过程。鉴于此，本文利用模糊综合评价法对提出的三种路基处理方案进行优选，以期得到理想的解决方案。

1 工程概况及地质条件

1.1 工程概况

曹妃甸综合保税区A21路全长1.244km，采用城市次干路标准进行设计，设计时速为40km/h，红线宽度为24m。

1.2 地质条件

A21路位于曹妃甸综合保税区内，该区域为新近围海造地而成，场地上部冲填土吹填时间较短，土质较为松软。依据钻孔揭露情况，可知拟建场地地层主要为海相沉积（）形成的粉土夹粉质黏土、粉质黏土夹粉土、粉砂层，其表层为冲填土（）。

按岩性特征、时代成因和物理力学性质指标，将场地划分为4个主要地层，分述如下：

（1）填土类

①杂填土：杂色，人工填筑形成，以山皮石或粉砂或黏性土为主，不同路段组成成分不同。厚度为1.0～2.8m，层底标高为1.85～3.48m。

②冲填土（以含细粒土砂混合较多粉土质砂为主）：灰褐色，土质不均，以粉砂、粉土为主，粉砂砂质不纯，松散，含大量黏粒及贝壳碎屑，局部夹杂黏性土。厚度为0.9～2.7m，层底高程为0.42～1.98m。

③冲填土（以高液限黏土为主）：褐灰色，土质不均，以黏性土为主，含大量粉粒及贝壳碎屑。局部以粉土为主并含有淤泥。厚度为0.8～3.3m，层底标高为-1.18～1.52m。

（2）粉土夹粉质黏土（低液限粉土）

褐灰色，高～中等压缩性，含腐殖质，见贝壳，夹较多粉质黏土薄层，粉土稍密，粉黏软塑～可塑。厚度1.7～5.1m，层顶高程为-5.01～-1.89m。

（3）粉质黏土夹粉土（低液限黏土）

褐灰色，软塑～可塑，含腐殖质，见贝壳，夹较多粉土或粉砂薄层，高～中等压缩性。

（4）粉砂（粉土质砂）

灰褐或灰黄或浅灰色，稍密，饱和，中等压缩性，黏粒含量较高。局部夹薄层粉土或黏土。

勘察期间测得场地地下水埋深为0.8～2m，地下水标高为1.82～3.32m，场地主要含水层为第②、（2）、（4）层砂土或粉土（夹）层，相对隔水层为粉质黏土（夹）层，地基土渗透系数建议值见表1。

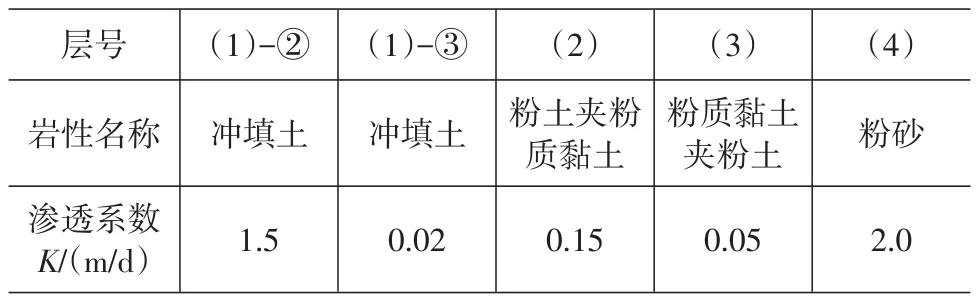
表1 地基土渗透系数建议值

2 模糊综合评价模型的建立

模糊综合评价基于层次分析法进行评价，利用模糊数学理论中的模糊运算法则，对非线性的评价论域进行量化综合，并结合改进的3标度层次分析法[1-3]，两者相辅相成，提高了评价的可靠性与有效性。

设因素集为U={ }u1,u2,…,un，元素 ui(i=1,2,…,n)是第1层（即目标层）中的第i个因素，由下一层中的m个子因素决定。根据每层中各个因素的重要程度，分别对每一因素给出相应的权数，依次得到各层次的因素权重集。评语集为V={ }V1,V2,…,Vp，对于每一因素的单因素评价，可看成下一层的多因素综合评价，分别计算各指标的相对隶属度，建立模糊评价矩阵R，采用改进的层次分析法确定各个模糊评价矩阵的权重系数A。利用2级模糊评价模型进行综合评价。

2级模糊评价的模型为：

式中：A为权重系数矩阵；R为模糊评价矩阵；rimp为元素uim隶属于评语集第p个元素的隶属度；B为目标层对于评语集的隶属向量；bn为模糊综合评价指标。

给定因素集U中的一对元素(xi,xj)具有某种特征的等级分别为 fxj(xi)和 fxi(xj)，如果xi、xj分别为方案Ci和Cj在对应指标上的反映，称[ ]fxj(xi),fxi(xj)为方案Ci和Cj分别在该指标上的二元相对比较级。定性指标分级量化见表2，方案相对比较量化见表3。

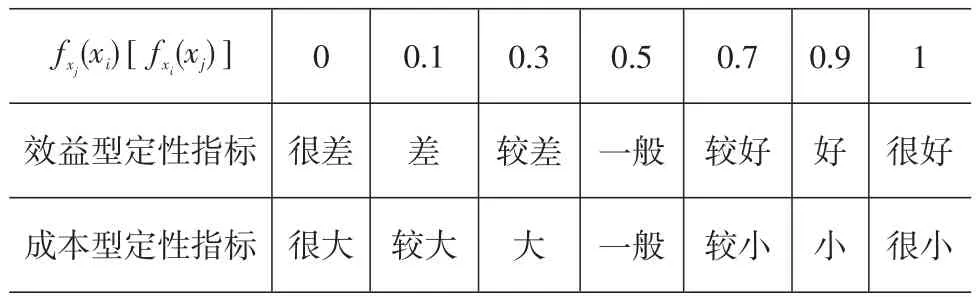
表2 定性指标分级量化表

表3 方案相对比较量化表

相对优先度： ρ(xi)=mi

jn f(xi|xj),(i,j=1,2,…,m)

在方案比选过程中，方案在各个定性指标上的相对比较级 fxj(xi)可由专家组经统计得出，运用上述公式可以计算出各方案对应于各定性指标的相对优先度。

对定量指标，可令方案Cj对应的第i个目标的第k个指标的隶属度表示为：式中：i=1,2,…,n，n为子集数；k=1,2,…,ni，ni为第i个子集中评价指标的数目； j=1,2,…,m，m为待优选方案数目。

采用上述方法将矩阵转化为如下隶属度矩阵：

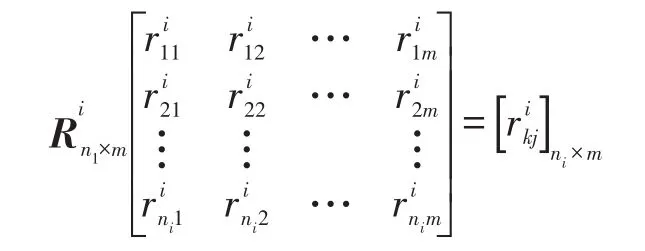
式中：k=1,2,…,ni;j=1,2,…,m。

优属度向量最优解模型为：

式中： p为广义距离参数， p=1为海明距离，p=2为欧氏距离。

通过确定各指标的隶属度来确定R，利用2级模糊综合评价方法最终得到各方案的权重系数，并依据最大隶属度原则选择最优方案。

3 评价指标体系的建立

建立科学合理的评价指标体系是方案选择模型建立的基础。本文在参考前人研究成果的基础上，结合路基施工的实践，以评价指标的科学性、层次性、完善性、适用性为原则，建立包括目标层、准则层和指标层在内的三层指标体系（见图1）。

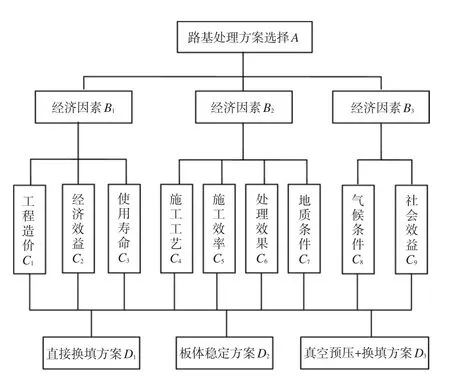
图1 评价指标体系

4 工程实例的计算分析

4.1 通过调查得出各判断矩阵

采用改进的3标度层次分析法（AHP），根据专家反馈结果，得出各判断矩阵。目标层A与准则层B各指标的判断矩阵见表4，准则层B与指标层C各指标的判断矩阵分别见表5～表7。

表4 A-Bj判断矩阵

表5 B1-Cj判断矩阵

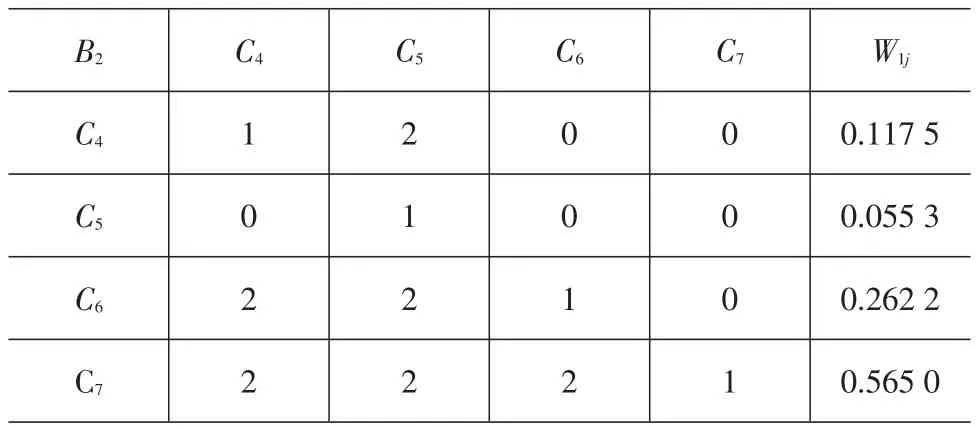
表6 B2-Cj判断矩阵

表7 B3-Cj判断矩阵

表4～表7中矩阵经计算C.R.均小于0.1，层次单排序具有满意一致性。

4.2 模糊隶属矩阵

准则层指标Bi的模糊隶属矩阵如下：

4.3 综合评价

由最大隶属度原则最终确定采用真空预压+换填方案。该工程综合考虑各方面的因素，经多次专家论证，最终确定采用真空预压为处理方案，与采用模糊综合评价方法得到的结果一致。

5 结论

本文采用模糊综合评价方法来评价和选择地基处理方案，优选方案时将影响方案选择的主观性转化为数学形式，同时考虑到各评价因素的权重，用相对优属度解决定性问题，模糊优选得到的结果与该工程最终采取的方案一致，因而具有更高的可靠性。

[1] 谢全敏，夏元友.边坡治理决策的改进层次结构模型及其应用[J].岩土工程学报，2002，24（1）：86-88.

[2] 王淼.天津市道路客运枢纽总体布局规划研究[D].天津：河北工业大学，2006.

[3] 许树柏.实用决策方法——层次分析法原理[M].天津：天津大学出版社，1983.

[4] L Mikhailov.Group Prioritization in the AHP by Fuzzy Preference Programming Method[J].Computer&Operations Research,2004,31（2）:293-301.

[5] C Mohan,H T Nguyen.Reference Direction Interactive Method for Solving Multiobjective Fuzzy Programming Problems[J].European Journal of Operational Research，1998，107（3）：599-613.