计量经济学课程论文写作实践研究——以中国工业总产值模型为例

黄 伟

（青海民族大学经济学院，青海西宁 810007）

1 问题的提出

找出影响中国工业总产值的相关因素。

2 理论模型设计

2.1 确定模型所包含的变量

据前人的研究，初步认为影响中国工业总产值的因素有资产总额和职工人数，即将资产K和职工人数作为解释变量L，将中国工业总产值Y作为被解释变量：Y=f（K，L）。

2.2 确定模型的数学形式

将模型暂先设定为：Y=AKαLβeμ。

3 样本数据来源

表1为中国某年按行业分的全部制造业国有企业及规模以上制造业非国有企业的工业总产值Y、资产合计K及职工人数L。

由图1和图2可知，Y与K、Y与L都不是呈现直线的形式，均属非线性关系，故可将模型设定为指数形式：

4 非线性回归模型转化为线性回归模型

式（1）经对数变换，可用如下双对数线性回归模型表示：

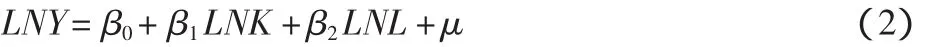
其中，β0=lnA，β1=α，β2=β。

5 参数估计及统计检验

对式（2）采用普通最小二乘法进行回归，Eviews 6.0软件的输出结果如表2所示。下面的式（3）给出了通常的报告式：

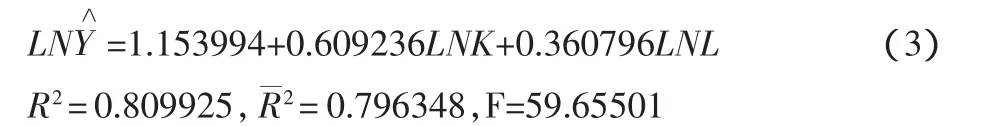
5.1 拟合优度检验

R2=0.796348表明，工业总产值对数值的79.6348%的变化可以由资产对数值和职工人数对数值的变化来解释，但仍有20.3652%的变化是由其他因素的变化影响的。

表1 中国某年工业总产值、资产合计和职工人数数据表

5.2 变量的显著性检验

在5%的显著性水平下，自由的为28的t分布的临界值为t0.025（28）=2.048，因此，lnK的参数通过了该显著性水平下的t检验，但lnL未通过检验。如果设定显著性水平为10%，t分布的临界值为t0.05（28）=1.701，这时lnL的参数通过了显著性水平。

5.3 方程总体线性的显著性检验

给定显著性水平1%，自由的为（2，28）的F分布的临界值为F0.01（2，28）=5.45，因此总体上看，lnK，lnL联合起来对lnY有着显著的线性影响。

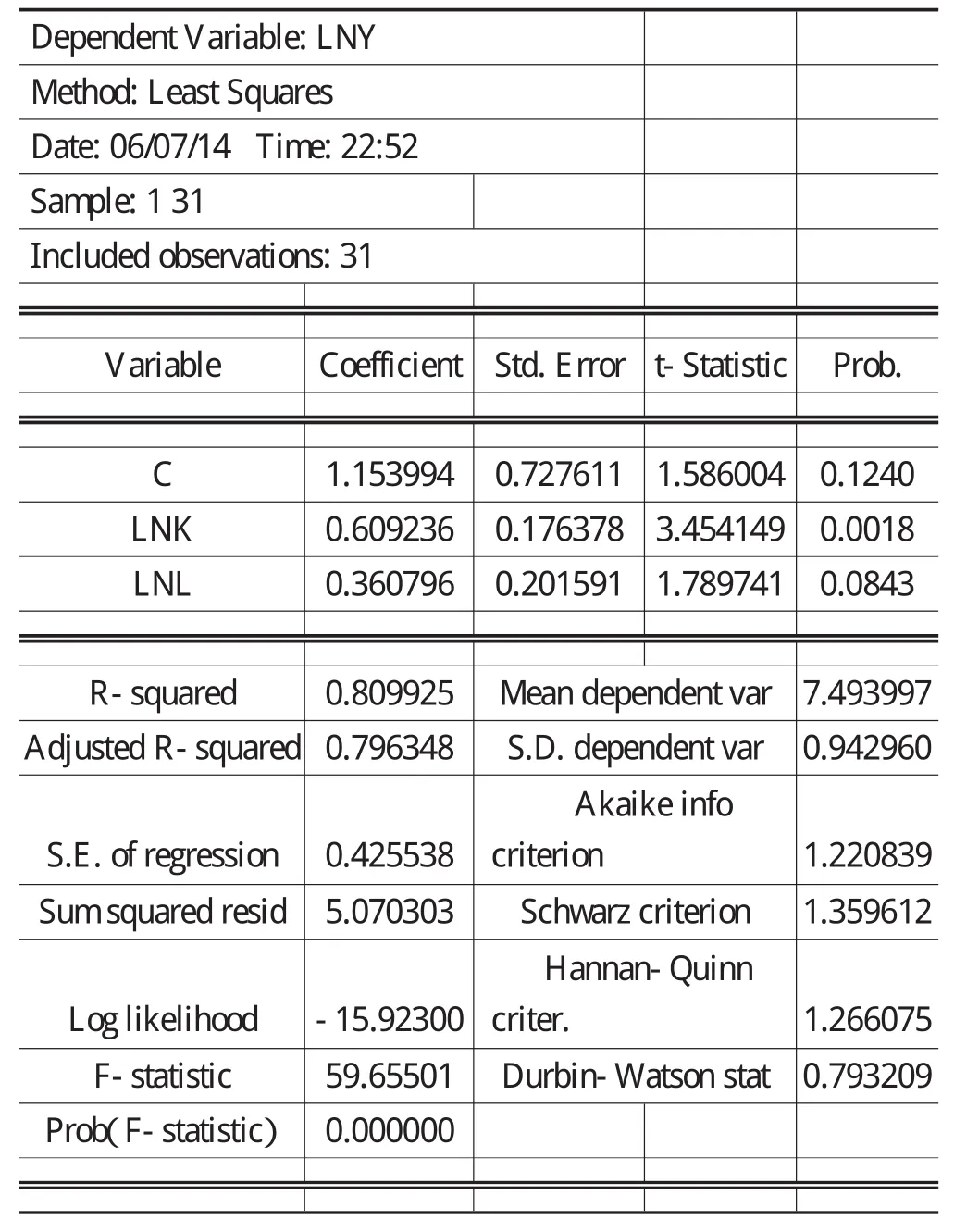
表2 参数估计结果

图1 Y与K的非线性关系图

图2 Y与L的非线性关系图

6 计量经济学检验

6.1 异方差性

6.1.1 图示检验法

由式（3）可知，影响工业总产值对数值的主要因素是资产对数值，因此，若式（2）存在异方差性，则可能是lnK引起的。式（2）经普通最小二乘回归得到的式（3）中残差平方项e～i2与lnK的散点图表明（见图3）：式（2）不存在异方差性；由图4也可知，式（2）不存在异方差性。

6.1.2 怀特（White）检验

因为怀特检验不需要排序，操作简便，且对任何形式的异方差都适用，适用性强，故选择其作为判断异方差性的依据。记为对原始模型（2）式进行普通最小二乘回归得到的残差平方项，将其与LNK，LNL及其平方项与交叉项作辅助回归，得：

怀特统计量nR2=3.651397，该值小于5%显著性水平下、自由度为5的x2分布的相应临界值x0.052=11.07，因此，不拒绝同方差的原假设。

去掉交叉项后的辅助回归结果为：

怀特统计量nR2=3.64281，因此，在5%显著性水平下，仍是不拒绝同方差的原假设。

6.2 序列相关性

一般的经验，对于采用时间序列数据作为样本的计量经济学，往往存在序列相关性问题；而截面数据一般不存在序列相关性问题，故在此未经检验直接假设模型不存在序列相关性问题。

6.3 多重共线性

6.3.1 检验简单相关系数

LNK，LNL的相关系数如表3所示。由表3可以发现LNK与LNL间存在高度相关性。

6.3.2 找出最简单的回归形式

分别作LNY与LNK，LNL的回归：

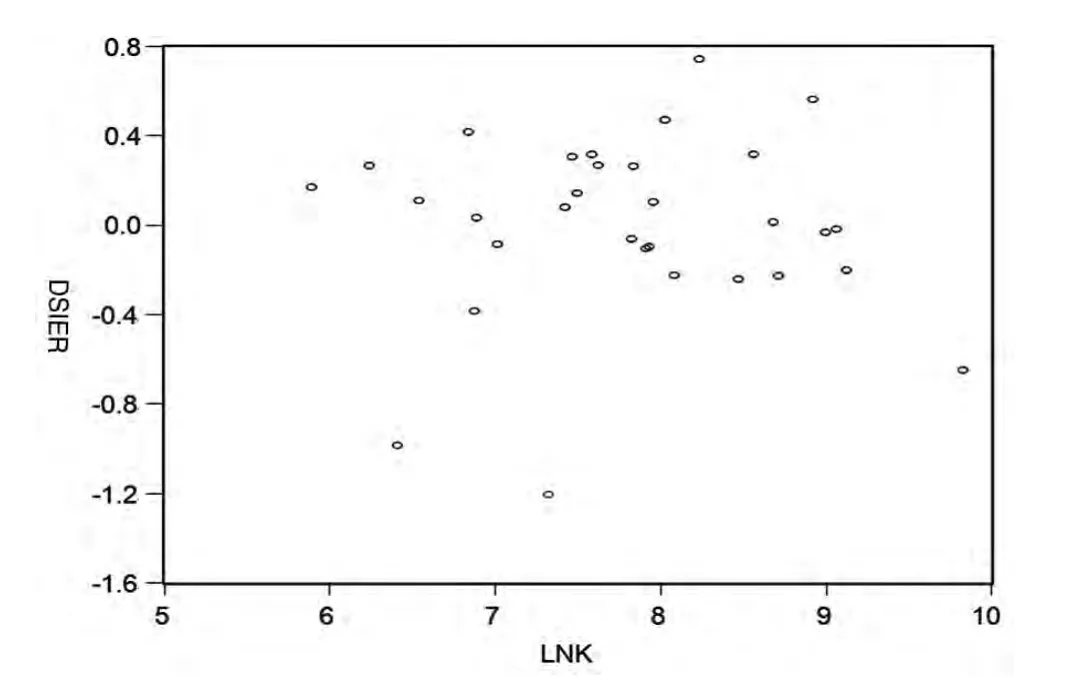
图3 异方差性检验图

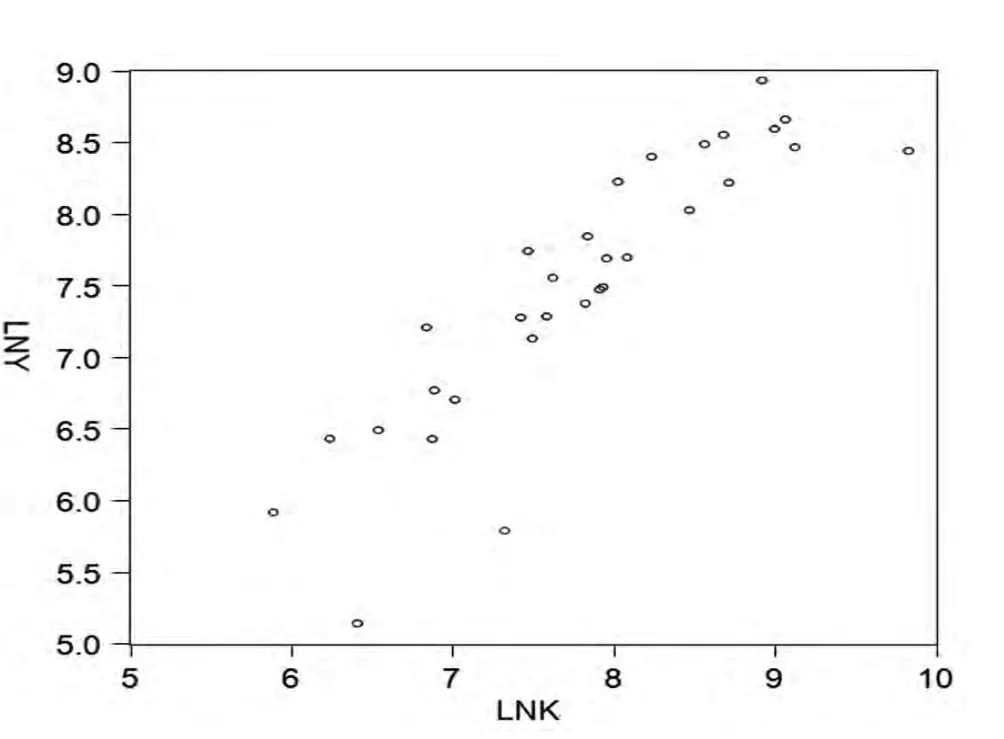
图4 同方差类型

表3 相关系数表

R2=0.728931

由于LNK的t统计量大于LNL的t统计量，所以用LNK来解释LNY更有说服力；且式（6）比式（7）的R2值大，说明式（6）的拟合优度更好，LNY更有可能是由LNK来解释；再者，由（3）知LNK对LNY的解释力更强。因此，将式（6）作为初始的回归模型。

6.3.3 逐步回归

将LNL导入上述初始回归模型（6）可得回归结果（3）式。对比这2个式子的回归结果可知：在初始模型中引入LNL，模型的拟合优度提高，且参数符号合理，变量通过了t检验，方程总体线性的显著性检验也通过了。因此，工业总产值函数应以LNY=f（LNK，LNL）为最优，拟合结果如式（3）。

7 受约束回归

从式（3）回归结果看，α =β1=0.609236，β=β2=0.360796，α+β=0.970032≈1，即资产与劳动的产出弹性之和接近1，表明中国制造业在该年基本呈现规模报酬不变的状态。下面进行参数的约束检验，检验的原假设为：α+β=1。若原假设为真，则可估计如下模型：

通过上述资料，估计结果如下：

容易看出，该估计方程通过了F检验与t检验。

无约束回归模型式（3）的残差平方和RSSU=5.070303，受约束回归模型式（8）的残差平方和RSSR=5.088613，样本容量n=31，无约束回归模型解释变量个数KU=2，无约束回归模型解释变量个数KR=1，约束条件个数为KU-KR=2-1=1。于是，在原假设为真的条件下，有：

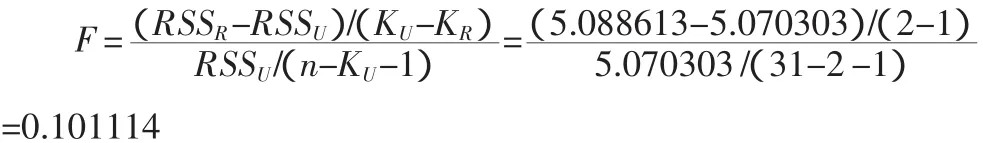
在5%的显著性水平下，自由度为（1，28）的F分布的临界值为4.20,计算的F值0.101114小于临界值4.20，不能拒绝假设，表明该年中国制造业呈现规模报酬不变的状态。在Eviews软件中的输出结果如表4所示，表明得出的结论仍是不拒绝原假设，即接受 α+β=1。

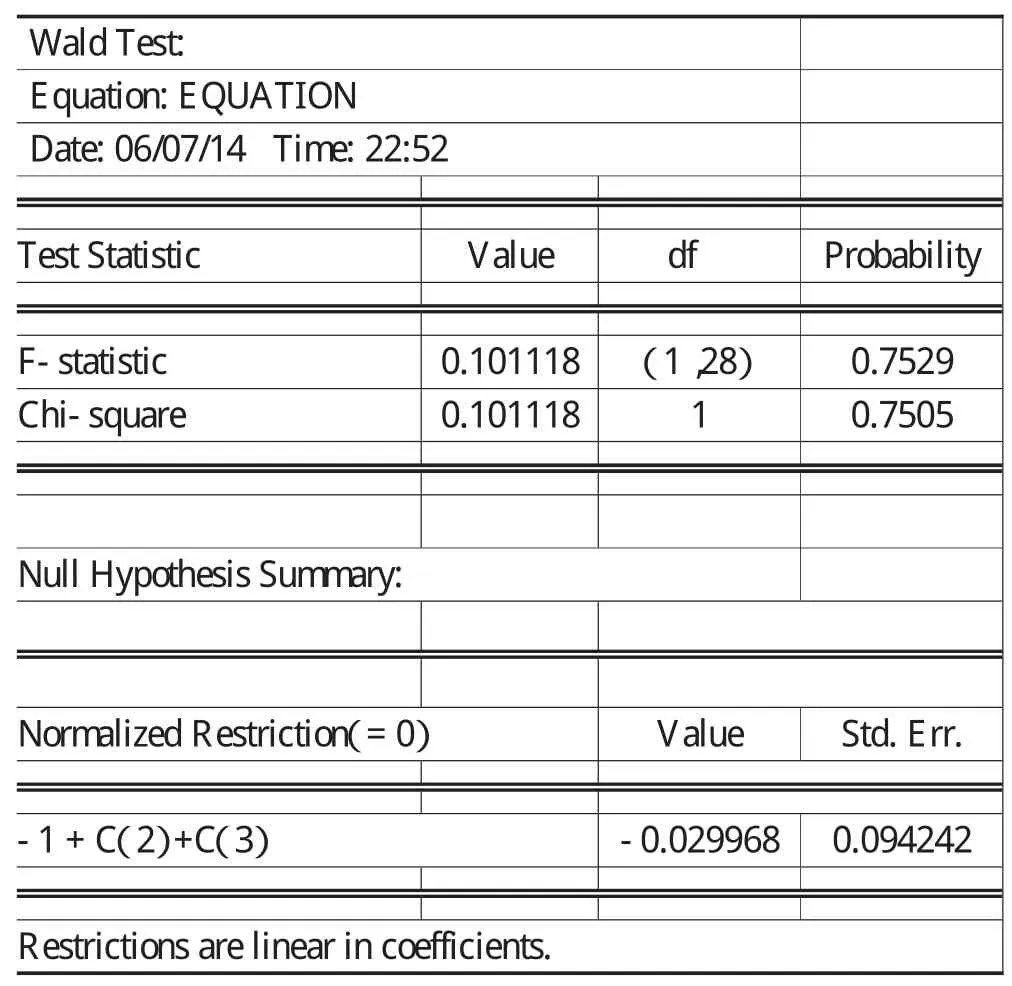
表4 受约束回归表

8 结论

（1）影响中国工业总产值的因素有资产总额和职工人数，三者的关系为非线性的，样本回归模型为LNY∧=1.153994+0.609236LNK+0.360796LNL。（2）该年的中国制造业基本呈现规模报酬不变的状态。