泊松分布参数的稳健估计

李洪明

泊松分布参数的稳健估计

李洪明

呼伦贝尔学院数学科学学院,内蒙古呼伦贝尔021008

本文主要以非对称分布中泊松分布为研究对象,探讨了其参数的稳健估计方法.作者以截断似然估计为基础,结合Cizek的工作,提出了适用于泊松分布参数的一种稳健估计方法.该方法避免了事先选取截断比例的麻烦,通过数据自身的信息给出在平均似然最大准则下的最优截断比例.在文中的模拟部分,分别就未受污染和受污染的泊松分布数据进行了模拟,得到了不错的效果.

自适应极大截断似然估计;泊松分布;崩溃点;稳健估计

对于非对称分布中的泊松分布而言,其在实际生活中有着十分重要的地位.很多的实际模型都是基于泊松过程提出的，然而在某个确定时刻，泊松过程就相当于是一个泊松分布。因此，如何估计泊松分布的参数在理论和实际中都有着重要意义.理论上，我们可以在估计泊松分布参数的方法基础上，考虑其是否适合于其它非对称分布的位置参数估计；实际中，较为准确地估计出泊松分布的参数对未来情况的预测有着重要作用。

Cizek在解决广义线性模型——Binary-Choice回归模型时，提出了一种通过数据自身情况决定截断比例的方法。本文就是在这个想法的基础上，通过一定的改进，提出了一种估计泊松分布参数的方法，并说明了该方法在估计泊松分布参数时的可行性。

1 泊松分布的参数估计

1.1极大似然估计

对于泊松分布而言，其分布律记为 p（ x;λ）,其中λ为待估的参数。假设X1,L,Xn是服从分布p（ x;λ）的独立样本。称由(1)式确定的MLE为参的极大似然估计。

因此，在泊松分布中，其参数的极大似然估计就是统计量x，从该表达式,我们可以发现当数据中有一个坏数据(即离群值)的时候，该表达式会与真实结果之间产生较大的偏差。对于泊松分布参数的极大似然估MLE而言，其方差n。另一方面，由Rao-Cramer不等式可知:对于任何无偏估计而言,其方差的下界为n。因此，在对泊松分布参数进行估计时，MLE是最有效的估计(即最小方差无偏估计)。进一步，由极大似然估计的近似分布性质可知：MLE具有近似分布N，n这也就是为什么在估计泊松分布的参数时常用极大似然估计的原因。

1.2M估计

对于分布p（ x;λ）而言，其中λ为待估的参数。假设X1,L,Xn是服从分布p（ x;λ）的独立样本，在正则条件下，λ的极大似然估计()MLEλ等价于方程(3)的解。

对于泊松分布而言，(3)式即为

令 ￢0 （u） =u，则泊松分布参数λ的极大似然估计λ(MLE)就是(5)的解。

对于(4)式而言，我们可以发现大数据xi对其影响很大。换而言之,如果数据被污染，有离群值在里面的话，那么用(4)式得到的估计会与真实值有较大偏差.我们称(6)式的解λ(MLE)为M估计。

进一步，考虑到数据的尺度问题，将(6)改进为

由M估计的近似分布性质可知：ME具有近似分布

Huber建议在(7)中取u和d如下：

1.3极大截断似然估计

Neykov和Neytchev基于极大似然估计的优良性质，提出通过似然函数截断一些可能的坏数据后再进行估计的方法，这种方法既保留了似然函数的部分性质，又提高了估计量的稳健性。

对于分布p（ x;λ）而言，其中λ为待估的参数，我们称(9)所对应的估计λ(MLE,h)为参数λ的极大截断似然估计。

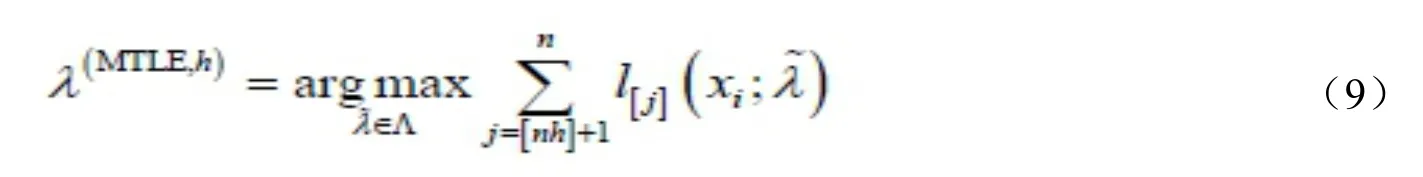
1.4自适应极大截断似然估计

基于1.3小节中提到的极大截断似然估计而言,它有一些不错的性质，但是截断比例h的选取并没有一致的方法。通常情况下,截断比例的选取依赖于一些先验知识。当h取得越大，则λ(MLE,h)受坏数据的影响越小，但有效性会降低。因此，我们考虑用平均似然达到最大的方法来确定截断比例h，称(10)所对应的截断比例h*为最优截断比例[1]。

其中λ(MTLE,h)的定义如(9)所示δλ为对截断比例上限的限制令λ(AMTLE,h)=λ(MTLE,h*)称估计量λ(AMTLE)为自适应极大截断似然估计。在实际操作中，我们可以用下面的方法来给出我们首先用样本的中位数median｛ xi｝作为位置参数λ的估计，记u=median｛ xi｝然后令我们来解释为什么这样选取λδ根据定理1，我们可以看出受数据影响较小的中位数在样本量趋于无穷的时候，虽然不是无偏估计，但其和真实值之间的差异并不太大。在样本量充分大时候，用上面所给的λδ作为截断上限可以保证得到的估计与λ相差不大[2]。

2 自适应极大截断似然估计的性质

2.1自适应极大截断似然估计的极限性质

根据(10)关于自适应极大截断似然估计中最优截断比例的定义，我们可以知道，当样本量n→∞的时候h*会以概率1趋于h0，h0有(11)式确定[3]。

根据引理1，我们可以得到λ(AMTLE)依概率收敛的极限，即下面的定理。

2.2自适应极大截断似然估计崩溃点

对于一个估计而言，我们常常考虑它受坏数据影响的情况。我们称一个估计是稳健的，是指它受坏数据影响较小[6]，即数据集中有坏数据和没有坏数据时的估计结果相差不大。但这种定义只是一个描述性的定义，对问题的分析没有太大的作用。Müller和Neykov[7]给出了一种描述一个估计稳健性的指标。在本文中，我们也用这个定义来描述估计的稳健性。

3 有限样本的性质

在这两个小节中，我们考虑的样本量n分别为100，200和400。对于相同样本量的数据，我们分别用极大似然估计，M估计，极大截断似然估计，自适应极大截断似然估计和中位数对泊松分布的参数进行估计。对于某一种估计结果，我们考虑它的均方误差MSE和平均偏差EB。这二者的定义如(13)所示。

在实际计算这两个指标时，我们采用Monte Carlo方法，用多次模拟的平均值近似真值。这由大数定律是可以保证的。为了提高估计的精度，在Monte Carlo方法的基础上，我们用Hammersley等减少方差的方法对模拟方法进行改进。

3.1未受污染数据的模拟

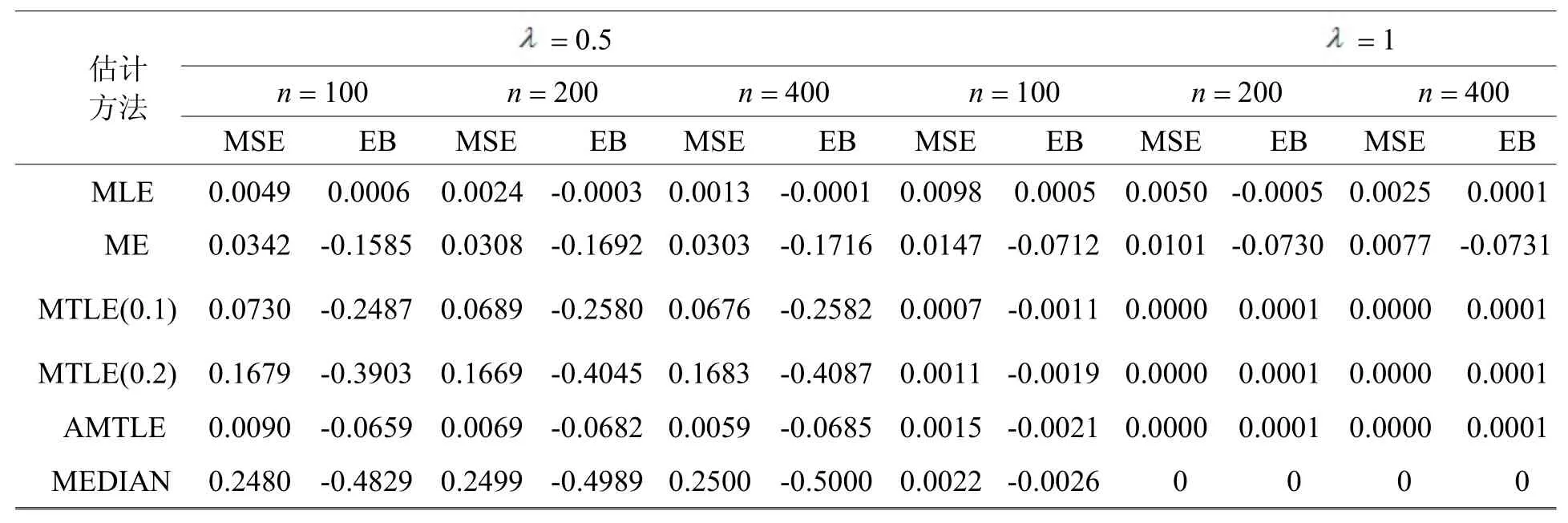
表1 未受污染数据的模拟情况Table 1 Unpolluted data simulation

=3.5 =4n=100n=200n=400n=100n=200n=400 MSEEBMSEEBMSEEBMSEEBMSEEBMSEEB MLE0.03530.00260.01770.00250.00870.00010.03980.00200.0202-0.00250.0100-0.0001 ME0.0982-0.0435 0.0683-0.0693 0.0441-0.10170.0485-0.07600.0282-0.08090.0170-0.0794 MTLE(0.1)0.1267-0.1080 0.0976-0.1403 0.0708-0.17160.0455-0.03160.0121-0.01090.0013-0.0015 MTLE(0.2)0.2136-0.2370 0.2192-0.3197 0.2236-0.39680.0738-0.05790.0218-0.02060.0026-0.0026 AMTLE0.0404-0.0707 0.0225-0.0710 0.0138-0.07260.04120.00890.01160.01260.00210.0096 MEDIAN0.2344-0.2668 0.2418-0.3464 0.2466-0.42240.0866-0.08540.0266-0.02890.0034-0.0038估计方法估计方法=21n=100n=200n=400n=100n=200n=400 MSEEBMSEEBMSEEBMSEEBMSEEBMSEEB MLE0.2054-0.00860.10330.00330.05070.00270.20990.00410.1058-0.00140.05250.0040 ME0.26260.05770.14950.05590.10150.05500.26940.07430.12670.04440.06120.0400 MTLE(0.1)0.3396-0.04090.2035-0.05720.1624-0.09280.3463-0.0218 0.1794-0.04940.0758-0.0372 MTLE(0.2)0.3983-0.08580.2412-0.09970.1926-0.13260.4021-0.0629 0.2204-0.08260.1008-0.0510 AMTLE0.2192-0.08290.1110-0.07010.0571-0.07120.2221-0.0683 0.1157-0.07570.0599-0.0709 MEDIAN0.4158-0.17960.2720-0.17800.2452-0.21540.4174-0.1623 0.2474-0.15780.1211-0.1075 =11n=100n=200n=400n=100n=200n=400 MSEEBMSEEBMSEEBMSEEBMSEEBMSEEB MLE0.10530.00330.0514-0.0063 0.02520.00250.11120.00190.0548-0.00310.02680.0006 ME0.16010.04660.10710.02340.09450.02210.13490.04100.05260.02190.02600.0230 MTLE(0.1)0.2092-0.0551 0.1598-0.1044 0.1339-0.14440.1829-0.04090.0842-0.04740.0259-0.0213 MTLE(0.2)0.2488-0.1088 0.2042-0.1650 0.1953-0.22150.2214-0.09160.1134-0.09020.0380-0.0420 AMTLE0.1149-0.0699 0.0594-0.0808 0.0307-0.07120.1213-0.07220.0635-0.07890.0339-0.0752 MEDIAN0.2769-0.1738 0.2424-0.2282 0.2431-0.29740.2434-0.14740.1357-0.11760.0498-0.0515估计方法=10.5 =20.5

从表1中，我们可以发现：当数据未受污染时，自适应极大截断似然估计的MSE是较其他稳健方法而言是最小的，并且EB也不是太大，也就是说在未受污染的情况下，自适应极大截断似然估计有良好的表现。对于中位数估计而言，当位置参数很小或者非整数时，其估计效果不佳，比如在0.5λ=的时候，中位数估计的结果和零非常的接近，在很多样本中中位数就是0，这与实际是不相符合的。从这一点也能看出，自适应极大截断似然估计就中位数估计而言，有一定的改进作用。

4 结论

通过上面的分析，我们可以发现，自适应极大截断似然估计在估计泊松分布参数的时候，具有较好的稳健性质，并且该估计不用事先给定截断数据的比例，在实际运用中较为方便。

[1]涂冬生,成平.非截尾型L统计量的Bootstrap逼近[J].系统科学与数学,1989,9(01):14-23

[2]郑忠国.随机加权法[J].应用数学学报,1987,10(02):247-253

[3]涂冬生.L统计量的Bootstrap逼近[J].科学通报,1986(13):965-969

[4]周勇.L统计量的随机加权分布逼近及重对数律[J].湘潭师范学院学报,1991,12(6):7-18

[5]刘银萍,宋立新.Ⅱ型截尾情形下泊松分布参数的估计[J].吉林大学学报,2007,45(6):941-944

[6]宋立新,薛宏旗.一种Sieve极大似然估计的渐近性质[J].湘潭大学学报,2000,20(03):370-377

[7]Klugman S A,Panjer H H.损失模型从数据到决策[M].吴岚译.北京:人民邮电出版社,2009:350-370

[8]Biihlmann H.Mathematical Methods in Risk Theor y[M].Berlin:Spring er Verlag,1996:100-120

Robust Estimation of Parameter in Poisson Distribution

LI Hong-ming
Mathematics Institute,Hulunbeier College,Hulunbeier021008,China

This paper,the asymmetrical distribution of the Poisson distribution as an objective,discussed the estimation method of robust parameter.Author truncated likelihood estimation,combining Cizek's work,proposed a robust estimation method applying to Poisson distribution parameters.It avoided the hassle of pre-selected cutoff ratio,and gave their information through the data at an average maximum likelihood ratio criterion optimal truncation.In the analog part of the text,uncontaminated and contaminated Poisson distribution data were respectively simulated to get good results.

Adaptive maximum truncated likelihood estimation;Poisson distribution;collapse;robust estimation

O211.3

A

1000-2324(2014)04-0615-05

2013-01-24

2013-03-02

内蒙古自治区高等学校科学研究基金项目(NJZY13319)

李洪明(1962-),男,副教授,河北保定人,研究方向:概率统计、数学模型.E-mail:li-h-m@163.com