结构动力弹塑性与倒塌分析(I)*——滞回曲线改进、ABAQUS子程序开发与验证

柳国环，练继建，国 巍

(1.天津大学建筑工程学院，天津300072;2.天津大学水利工程仿真与安全国家重点实验室，天津300072;3.中南大学土木工程学院，湖南长沙410075)

0 前言

当今，随着经济的快速发展和社会的不断进步，大跨和超高层等超限结构日益增多。根据当前的规范要求，超限结构的地震反应分析需要作为一项专门的工作来进行，如结构在大震作用下的动力弹塑性表现行为(叶献国等，2003;宣钢等，2003;杜修力等，2007)，然后对计算结果是否符合相关规范和(或)规程的相关具体要求进一步审查。一般情况下，对于这种特殊结构的计算通常需要用到非线性计算能力相对较高级的大型分析软件，例如:ABAQUS、MSC.MARC和LSDyna。柳国环等(2014a)针对ABAQUS大型程序，做了滞回规则改进、相关程序开发以及试验结果对比，并通过带有大跨—输电实际工程计算进一步检验了相关程序的可行性、计算精度与现实可靠性。

就ABAQUS大型软件而言，核心程序涉及到隐式和显式两种算法，隐式算法需要迭代计算以满足相应的容差，而显式算法无需迭代，但一般需要将步长设置为比较小(与结构体系中单元尺寸有关)以得到可靠可信的计算结果。在ABAQUS中，可以编制子程序并与主程序对接来实现结构的钢筋混凝土动力弹塑性分析，相应隐式和显式算法的接口子程序头文件分别为UMAT和VUMAT，采用UMAT和VUMAT中的已有变量参数直接与程序中需要额外定义变量共同实现相应本构子程序的代码。为此，本文首先根据已有资料详细回顾了钢材和混凝土材料的单轴本构模型，并改进了混凝土卸载后再加载曲线的规则，旨在使滞回曲线避免理论上存在加载曲线与卸载曲线在拐点前相交的可能性，并使得再加载曲线形状更接近于试验曲线形状(先凹后凸的曲线状)。然后，给出了ABAQUS中UMAT与VUMAT之间的区别与联系，并按照UMAT与VUMAT的规则开发了直接能够与ABAQUS主程序保持数据相互调用的显式和隐式算法子程序ABA-Subroutine。最后，将编制的子程序分别用于钢筋束、素混凝土、钢筋混凝土、型钢混凝土以及钢管混凝土构件的弹塑性分析中，并将计算结果与试验结果相对比，进一步考察和验证程序的可行性和准确性。本文关于ABAQUS子程序开发工作具有一定基础性，与柳国环等(2014b)的研究成果共同作为系列性工作，可为后续工作中计算结果的可靠性提供可行可信的前提条件。

1 材料本构关系

1.1 常用钢材滞回规则的3种情形

本节重点详述常用钢筋滞回曲线3种情形的加载卸载规则。骨架曲线与滞回曲线如图1所示(GB 50010－2010)。对于如图1b所示的滞回曲线的滞回规则如式(1)所示，相关参数意义如图1b中标注。

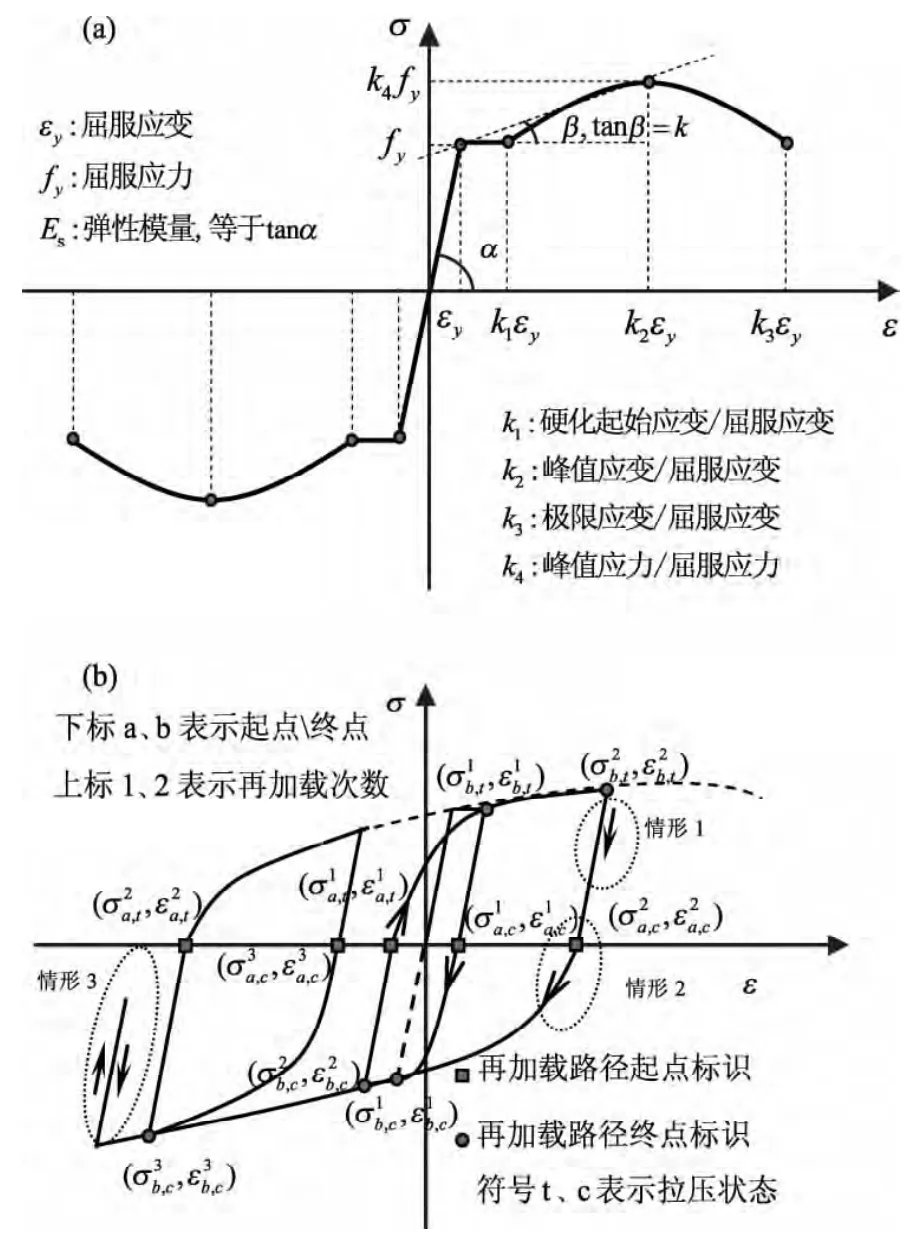
图1 钢材本构的骨架(a)和滞回(b)曲线示意图Fig.1 Envelop(a)and hysteristic(b)curves of steel constitutive

加卸载规则分3种情形说明:

(1)对于所有卸载:均按照弹性模量斜率计算。

(2)对于穿越平衡位置后的反向加载:εa和σa表示卸载后再加载路径起点的应变和应力，一般取为滞回曲线与横坐标的交点，这时σa=0。

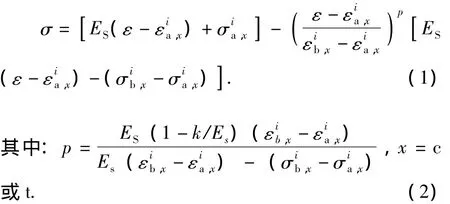
εb和σb表示卸载后再加载路径终点的应变和应力(初始值取为初始屈服点对应量值)，如果再加载方向的钢筋在加载历史进程中尚未发生过屈服，则εb和σb取钢筋初始屈服点的应变εb和应力fy，如果再加载方向的钢筋曾经有过屈服，则取该加载方向钢筋历史进程中的最大应变和应力。

(3)对于在平衡位置一侧的卸载后再加载:

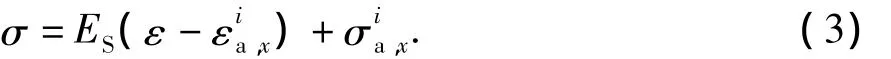
式中，σ和ε表示滞回曲线函数的因变量(应力)和自变量(应变)。k表示等效硬化斜率，一般取为峰值强度和屈服强度两点所确定直线的斜率tanβ(图1a)。上述处理方法旨在通过确定式(1)～(3)中的参数来最终确定此函数的表达式，以描述接近于实际钢材的反复加载下的物理行为。

1.2 反复受压卸载规则回顾与再加载规则改进

混凝土材料骨架曲线在低周反复荷载作用下的表现比较稳定，且与在单调荷载作用下的表现有很好的一致性。但是，由于混凝土材料自身的特性与组成相对复杂等原因，在低周反复荷载作用下的滞回曲线的表现与钢材相比更难以被准确量化。例如，由于加载过程中混凝土中局部发生裂纹等损伤现象，而且损伤会逐渐积累，会直接导致混凝土随后表现出来的刚度逐渐减小，即刚度退化。目前描述混凝土滞回曲线的规则颇为多见，限于一次加载卸载过程试验不能够考虑到多次反复荷载作用下混凝土的表现行为，然而这种反复加载卸载作用下表现行为更符合随机荷载作用下(例如:地震)实际情况。图2b为混凝土反复荷载作用下滞回曲线示意图，图中σ与ε分别表示应力和应变，下标un，s和un，e表示卸载始点和终点，下标l，m表示加载路径中的拐点，i和j表示第i次由骨架曲线卸载后第j次加载或卸载次数。

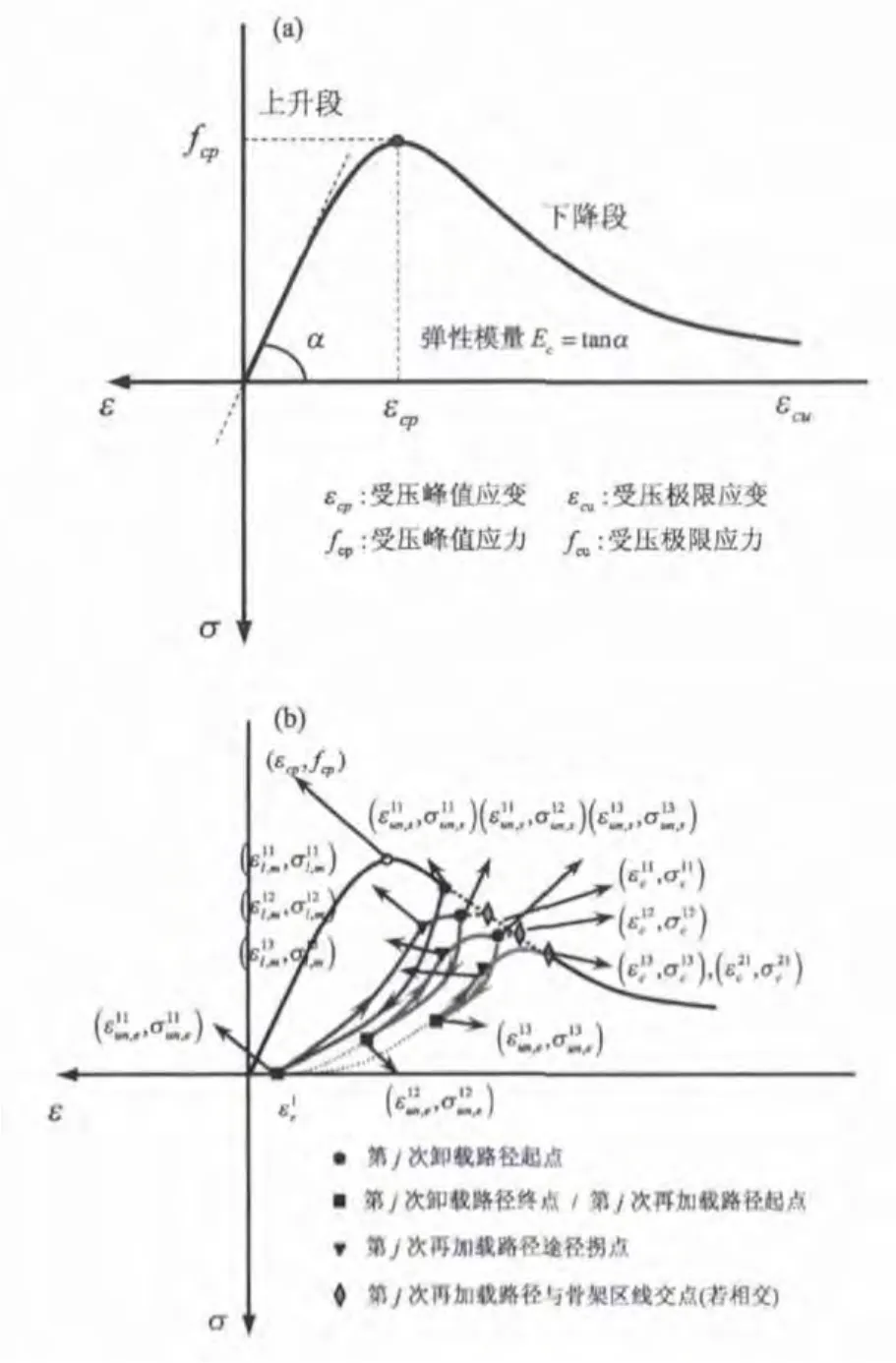
图2 混凝土单轴本构骨架(a)和滞回(b)曲线示意图Fig.2 Envelop(a)and hysteristic(b)curves of concrete umiaxial constitutive

(1)往复受压混凝土的卸载规则

为能够体现残余应变随加卸载次数增加而逐渐累计增大以及卸载刚度的逐渐退化(GB 50010－2010;聂建国，陶慕轩，2011)，按照如下计算:

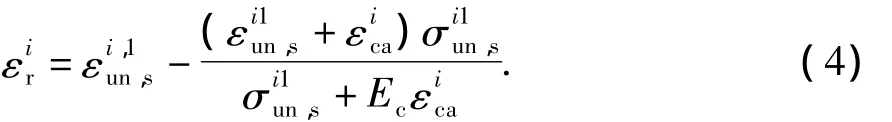
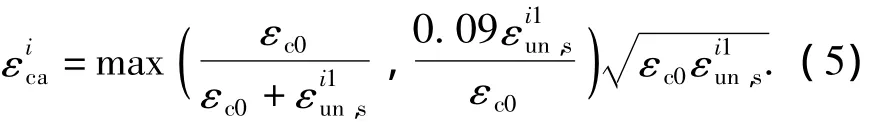
式中，εc0为混凝土的峰值压应变，根据(GB 50010－2010)取值。

本文未依据混凝土结构设计规范(GB 50010－2010)(GB 50010－2010)中所述直线卸载规则，而按照式(6)确定的更新割线刚度Eir后直接计算当前的应力。根据聂建国和陶慕轩(2011)通过卸载初始点应力、初始点应变、残余应变以及当前步的应变ε共同来描述卸载曲线，如式(7)所示。

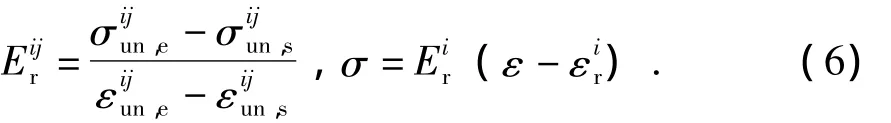
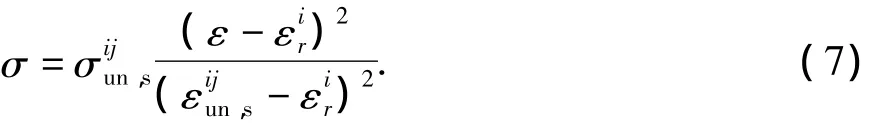
(2)往复受压再加载规则改进

与卸载路径不同，考虑到卸载后再加载路径曲线存在拐点(再加载过程中曲线先表现为凹形曲线而后形状发生变化的点)。本文同样分段考虑加载规则，但为了更好描述再加载曲线路径，这里定义为:第一段曲线凹(非二次曲线)，第二段曲线凸(非直线)，并给出拐点位置的应变和应力的规则如下:

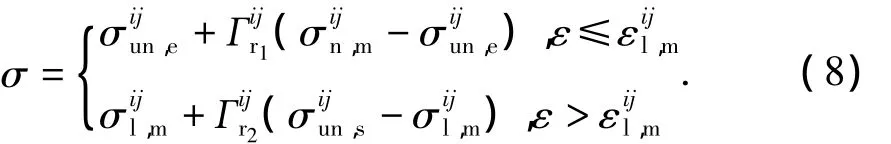
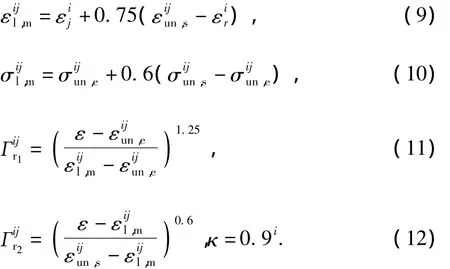
式(12)中，κ=0.9i定义为卸载后再加载段拐点之后刚度退化参数，与由骨架曲线上卸载的次数i有关，该值随i增大而减小。

需强调的是，编制程序时需要调用ABAQUS主程序中参数，需注意与上述表达式中物理参数符号统一。

2 子程序开发与实现

ABAQUS主程序具有用于二次开发材料接口的子程序，对应于隐式与显式算法的头文件为UMAT和VUMAT。用户可利用相应接口编制子程序，并按照本构关系滞回规则定义变量，通过调用主程序材料参数并与主程序状态变量实现无缝对接。关于子程序与ABAQUS主程序链接的基本框架如图3所示。

如图3a所示，对于采用UMAT的隐式算法需要更新应力、应变和相关的状态变量，还要更新本构的雅克比矩阵(应力增量对应变增量的导数(dΔσ/dΔε)，然后通过当前更新的雅克比矩阵、应变矩阵以及几何属性可得到单元刚度矩阵的增量，可得到当前步局部坐标系下的单元刚度矩阵，进而结合单元的局部与整体坐标系的关系形成结构的整体刚度矩阵，隐式运算需要迭代以满足相应的容差。

如图3b所示，对于采用VUMAT的显式算法子程序内部直接更新的物理量是应力和相关状态变量，因此不需要本构的雅克比矩阵。显式算法不需要迭代，但需要事先通过ABAQUS设置的计算步长应足够小以得到可靠可信的计算结果。这里需要强调，适为降低显式算法的VUMAT子程序可能的数值误差，相应变量宜被定义为双精度，同时使用real*8和include vaba_param.inc定义，若只采用include vaba_param.inc语句不能确保变量被承认为双精度，而与real*8共同使用具有双保险意义。此外Job中显式精度(ABAQUS/Explicit Precision)选为 double。对于 UMAT或 VUMAT，考虑应变率因素对本构动态强度提高影响，均需要通过应变增量DSTRAN与DTIME计算应变率绝对值DSTRAN/DTIME，然后根据本构动态提高系数公式进行计算。

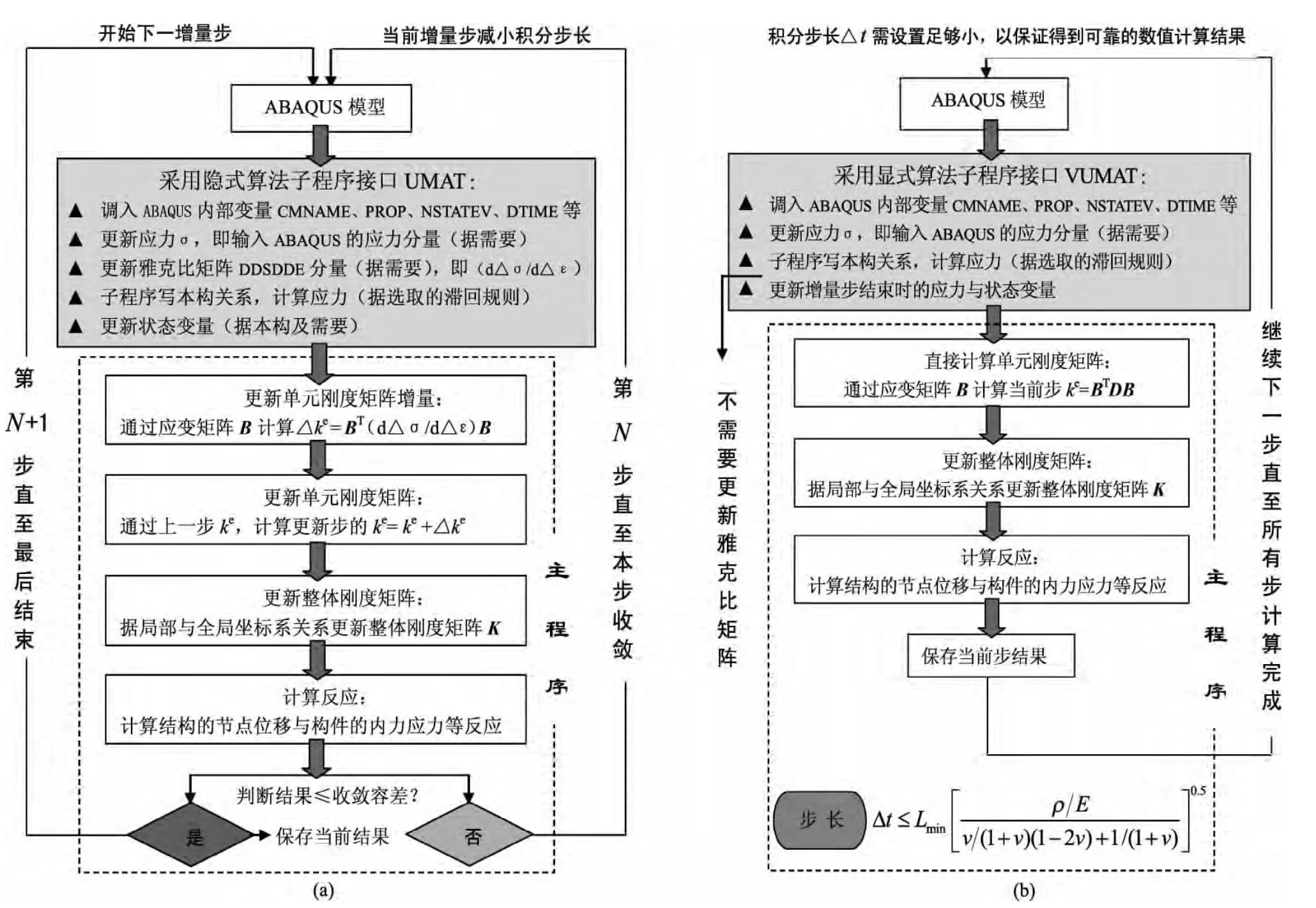
图3 ABAQUS主程序与子程序UMAT(a)与VUMAT(b)链接基本流程图Fig.3 The basic flowchart of main program ABAQUS link to subroutine program UMAT(a)and VUAMT(b)

3 试验验证——钢筋和素混凝土

为检验上述开发程序的可靠性，首先需要分别对钢筋与混凝土代码的准确性进行验证。

验证钢筋计算结果:如图4a所示的钢筋位移加载制度根据应变—位移加载曲线以及试验样本标距给出(李敏，2012;李敏，李宏男，2010)，用于ABAQUS位移方式加载。分析时，ABAQUS中的隐式算法为采用静力分析，显式算法采用加大阻尼的动力计算方法(显式算法只有动力分析，下同)以得到静力计算的效果，与李敏(2012)给出的进入屈服阶段后三周的滞回环结果相对应，相应给出了后3周的数值结果，两种算法的结果与试验结果对比曲线如图4b所示。本文中钢筋与其他算例相比尺寸较小，故显式算法最大步长较取为1.0E－7。

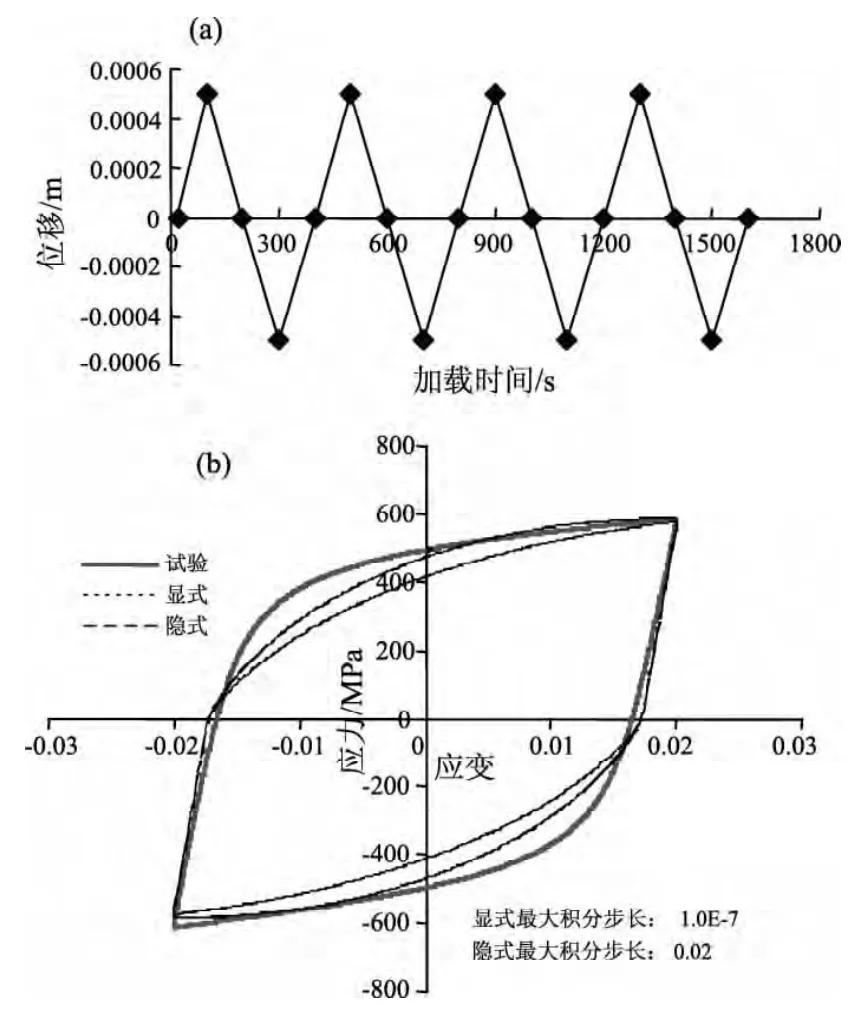
图4 钢筋束加载制度与试验结果对比(a)对应于试验应变加载的等幅值位移加载曲线;(b)数值计算与试验结果对比Fig.4 Loading system of steel bar HRB400 and test results comparison(a)amplitude displacement loading curve corresponding to the test strain loading;(b)comparison betweeen numerical calculation and test results

验证素混凝土代码计算结果:以编号BII－6试件为例，为100 mm×100 mm×300 mm棱柱体(过镇海，张秀琴，1981)。试验应变增量控制为1.0E－3(每次位移加载的增量为3.0E－1 mm)，每次卸载至应力为零结束后再反向加载，在第9次(应变为9.0E－3)开始卸载至应力为零时结束。加卸载曲线依据1.2节所述规则。为考察混凝土加卸载规则以及代码的计算精度，应力—应变曲线(骨架曲线)按照过镇海和张秀琴(1981)取为

式中，峰值应力σ1取值为30.664 MPa，峰值应变ε1取值为1.486E－3;a和α为参数，据过镇海和张秀琴(1981)表2取值分别为1.2和1.64，b=3－2a，c=a－2。

两种算法的结果如图5b所示，两者结果相近，与图5a所示的试验结果对比具有较好的一致性。

4 试验验证——钢管/型钢/钢混构件

图6a～c依次给出了圆钢管混凝土、型钢混凝土以及钢筋混凝土构件的示意图，并给出了相应的边界条件、几何参数与材料参数(李敏，2012;李敏，李宏男，2010;过镇海，张秀琴，1981;刘文渊等，2012，周绪红等(2009)，加载制度如图6d～f所示。

首先采用SAP2000软件分别建立上述3种构件的有限元模型，然后采用柳国环等(2014a)中SAP2ABAQUS接口程序分别ABAQUS的inp文件，文件格式包括相应隐式和显式格式。进而应用ABAQUS读入inp文件调整模型，转换前后的有限元模型与相应说明如图7所示。分别采用隐式和显式算法分析图中算例，并将模拟结果分别与文献中试验结果相比较，比较结果见图8。应该说明，图7～8和9中模型试验数据由提取数据的Getdata软件获取得到，显式和隐式方法计算最大步长设置为1.0E－6和0.02。

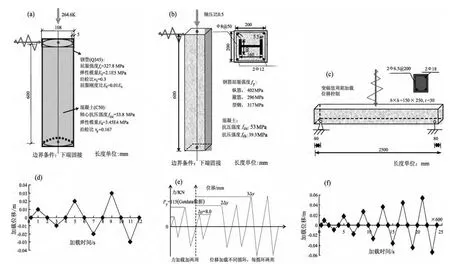
图6 模型示意图与加载历程(a)圆钢管;(b)型钢;(c)钢筋;(d)圆钢管混凝土构件加载曲线;(e)型钢混凝土构件加载曲线图;(f)钢筋混凝土构件加载曲线Fig.6 Model diagrammatic sketch and its corresponding loading history(a)circular steel tube;(b)section reinforced;(c)reinforced;(d)loading curve of concrete filled steel tube column;(e)loading curve of SRC column;(f)loading cauve of RC beam

图7 SAP模型(a)与采用SAP2ABAQUS转化后的ABAQUS模型(b)Fig.7 Comparison between SAP model(a)and ABAQUS model obtained by using SAP2ABAQUS(b)对比

从图8a、9a和10a中可以看出:采用显式与隐式方法的计算结果比较一致，说明在合理选择步长情况下，不同算法对计算结果的影响较小。从图8b、9b和10b中，可以看出:数值计算与试验获取数据结果接近程度令人满意。需要说明的是，考虑到李敏和李宏男(2010)研究中型钢混凝土给出了位移加载曲线周期数(6周)和重复循环次数(每2周采用同一等幅加载)，因此在提取其试验数据时也只提取至位移加载的第6周(所显示的第3个滞回环)加载结束。

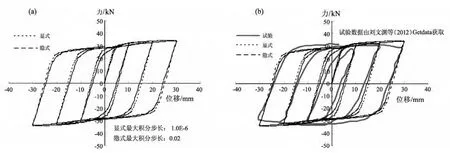
图8 圆钢管混凝土构件计算结果(a)显式与隐式结果对比;(b)显式、隐式与试验结果对比Fig.8 Calculation results for concrete filled circular steel-tube column(a)comparison between explicit and implicit results;(b)comparison among explicit，inplicit and test results

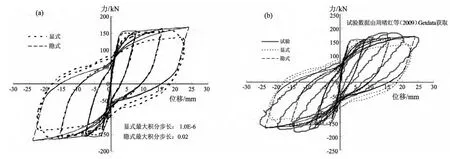
图9 型钢混凝土构件计算结果(a)显式与隐式结果对比;(b)显式、隐式与试验结果三者对比Fig.9 Calculation results for SRC column(a)comparison between explicit and implicit results;(b)comparison among explicit，inplicit and test results

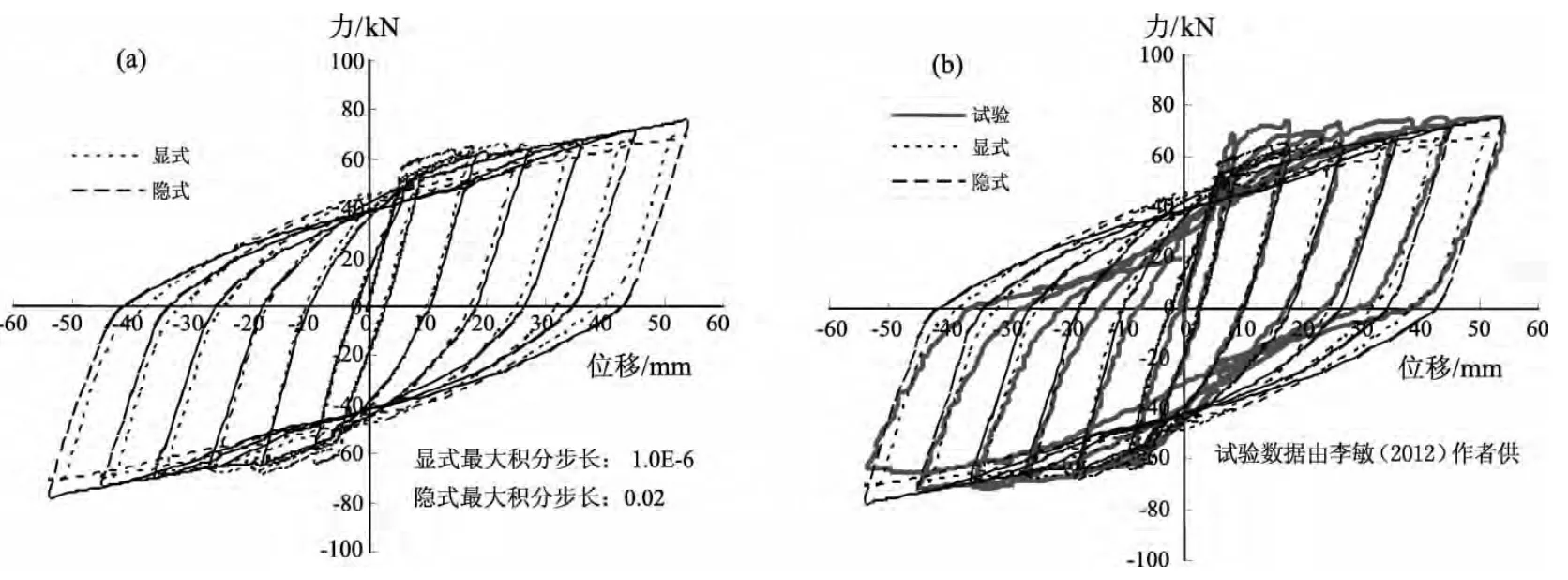
图10 钢筋混凝土构件分析结果对比(a)显式与隐式结果对比;(b)显式、隐式与试验结果三者对比Fig.10 Comparison of analysis results for RC beam(a)comparison between explicit and implicit results;(b)comparison among explicit，inplicit and test results

5 结语

本文作为系列研究的第I部分工作，主要涉及本构与子程序开发等方面内容，简要总结如下:

(1)改进了混凝土卸载再加载曲线规则并给出具体表达式，定义了再加载段拐点之后刚度退化参数。

(2)给出并重点论述了UMAT和VUMAT与ABAQUS链接的框架示意图，并给出相关注记。

(3)开发并实现了适用于隐式算法UMAT的子程序以及适用于显式算法的双精度VUMAT的子程序。

(4)验证了本文改进的混凝土再加载规则与所开发程序的可行性和计算精度。首先考察了两种算法(隐式和显式法)对单一材料(钢筋和素混凝土)构件的计算结果，进而考察了对混合材料(钢筋混凝土、钢管混凝土和型钢混凝土)的计算结果，并与试验结果相对比。

本文的理论基础和本构改进、程序开发以及试验验证，可为实际工程计算提供可靠性保证。

杜修力，贾鹏，赵均.2007.钢筋混凝土核心筒不同轴压比作用下抗震性能试验研究［J］.哈尔滨工业大学学报，39(2):567－572.

过镇海，张秀琴.1981.混凝土在反复荷载作用下的应力—应变全曲线［J］.冶金建筑，9:14 －17.

李敏.2012材料的率相关性对钢筋混凝土结构动力性能的影响［D］.大连:大连理工大学.

李敏，李宏男.2010.建筑钢筋动态试验及本构模型［J］.土木工程学报，43(4):70－75.

刘文渊，冷杰，段文峰.2012.往复荷载下圆钢管混凝土柱的数值模拟［J］.吉林建筑工程学院学报，29(1):1－4.

柳国环，练继建，国巍.2014a.结构动力弹塑性和倒塌分析(II):SAP2ABAQUS接口技术、程序开发与验证［J］.地震研究，37(1):132－140.

柳国环，练继建，孙雪艳，等.2014b.结构动力弹塑性和倒塌分析(III):地震差动作用下输电塔—线体系的弹塑性与倒塌分析［J］.地震研究，37(1):141 －150.

聂建国，陶慕轩.2011.采用纤维梁单元分析钢—混凝土组合结构地震反应的原理［J］.建筑结构学报，32(10):1－10.

宣钢，顾祥林，吕西林.2003.强震作用下混凝土框架结构倒塌过程的数值分析［J］.地震工程与工程振动，23(6):24－30.

叶献国，徐勤，李康宁，等.2003.地震中受损钢筋混凝土建筑弹塑性时程分析与振动台试验研究［J］.土木工程学报，36(12):20－25.

周绪红，张小东，刘届鹏.2009.钢管约束钢筋混凝土柱与型钢混凝土柱滞回性能试验研究［J］.建筑结构学报，30(supp1):121－128.

GB 50010－2010，混凝土结构设计规范［S］.