基于多目标拓扑优化的失效零件再设计

孙 哲，胡于进

（华中科技大学机械科学与工程学院，湖北 武汉430074）

0 引言

在当今的工业设计中，零部件结构创新设计和轻量化设计成为当前机械设计的一个重要的方向。拓扑优化已成为实现零部件结构创新设计和轻量化设计的重要工具，被广泛运用于建筑、航空航天、汽车、海洋工程和船舶制造等领域［1－2］。

近些年来，拓扑优化的应用逐渐增多［3－5］。但是，参考文献［3－5］都是通过选择一个主要目标进行单目标优化，没有考虑到在复杂多工况多目标情况下的拓扑优化设计。由于设计问题的复杂性，必须满足的设计指标往往是多方面的，因此，多目标优化是工程设计的一个基本问题。在多目标拓扑优化中，孙晓辉［6］，范文杰［7］等提出运用数学规划法将多目标的拓扑优化问题转换为单目标的拓扑优化，通过加权规划法将多目标的拓扑优化转变为单目标优化，但是如何选择合适的权重仍是一个难点。

耿玉磊［8］等总结了求解多目标优化的几种方法，提出将模糊理论和满意度应用于多目标优化中。基于这一思想的启示，结合模糊理论，提出了一种基于模糊满意度和加权平方和法的变权重多目标拓扑优化，利用子目标函数的模糊满意度构造其权重，实现了各子目标函数权重的动态调整，解决了权重难以选择的问题。

1 基于模糊满意度的变权重多目标规划方法

1．1 模糊满意度

模糊理论是处理不确定问题的理论基础，已成为解决多目标优化问题的一种有效工具，其基本思想是将目标函数模糊化，引入隶属度函数，将优化目标的最优解转换为寻找目标模糊集中的满意解。假设多目标优化问题表达为：

用各个约束条件对各个单目标fi（x）进行优化（式（2）），求解得到该目标的最优解以及其他目标函数的值，结果如表1所示。

表1 单目标优化结果

表1矩阵对角线的元素fii（x）即fi（x）目标的理想点，定义表1各列中离理想点最远的点为，并为目标fi（x）的悲观点。和组成理想点和悲观点向量，多目标优化的过程就是在理想点和悲观点组成的n维长方体中寻找满意解［9］。

将子目标函数模糊化，对于每个目标函数fi（x），i＝1，2，…，n，给出相应的模糊伸缩指标di（di＞0）。伸缩指标的取值根据该目标可以接受的最差解与理想解的差值来选择，定义目标函数隶属函数格式为［10］：

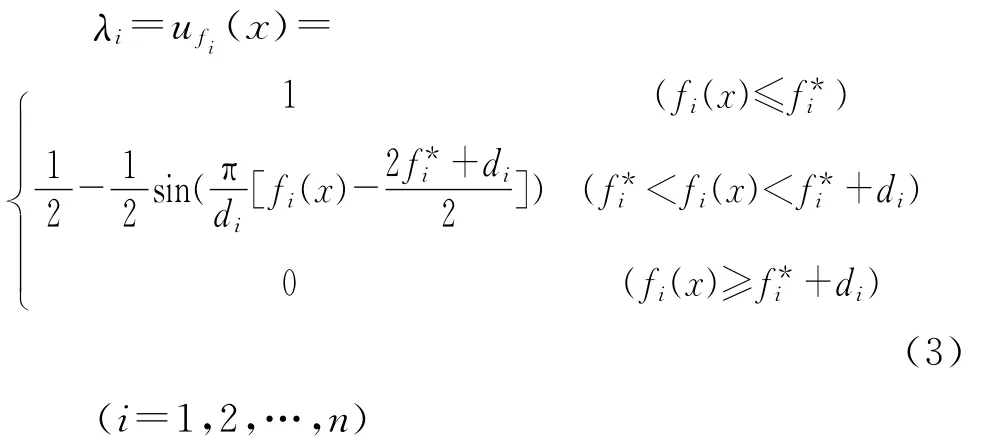
隶属函数值λi反映了目标函数fi（x）的值在该目标的模糊集中接近理想点的程度，定义λi为第i个目标的模糊满意度，表示该目标在模糊目标集的隶属程度。

1．2 基于模糊满意度的变权重多目标规划法

加权平方和方法是求解多目标优化的一种常用的方法，对于1．1节所给的多目标优化构造出加权平方和法的评价函数为：

根据式（3）的模糊满意度来确定各个子目标的权重，权重会根据子目标函数值确定，此时权系数wi是动态的。选择权系数为：

使用模糊满意度来确定加权系数，可以根据各个目标在模糊集中的满意度来动态地调整目标的权重，满意度较小的目标权重加大，使该目标可得到较好的优化。此外，子目标模糊化的伸缩指标是通过每个目标可接受最差解来确定的，这样可以控制优化后的各个目标值尽量落在自己期望的范围之内。

1．3 多目标拓扑优化

在多工况下，每个工况都对应着一个刚度最优的拓扑形状。因此，多工况刚度优化问题属于多目标拓扑优化。通常把刚度最大问题转化为柔度最小问题来处理来定义，柔度则用应变能来定义。

多工况的刚度最大化拓扑优化问题描述为：

fj为最小的第j阶模态；v为优化后的体积比，用来控制优化得到的最大体积。

每个工况的刚度最大化优化模型为：

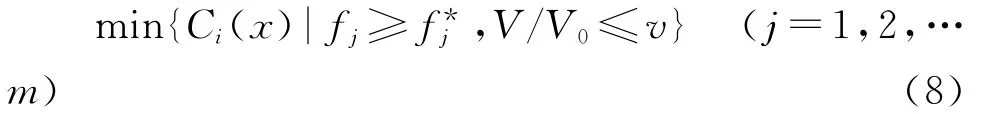
由于零件轻量化设计成为当前设计工作的一个需要考虑的因素，所以体积最小化也要作为一个设计目标。体积最小化问题一般描述为：

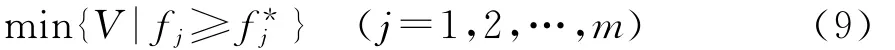
根据式（3）写出各个目标函数的隶属函数为：

在Optistruct中求解单目标优化（8）和（9），得到如表1所示的矩阵表。确定理想点和V＊，悲观点和Vmax，根据各个目标函数允许的最差解，选择合适的伸缩指标di和dV。由式（10）和式（11）得到模糊满意度的表达式，由式（4）和式（5）得到多目标拓扑优化的评价函数为：

多工况和体积的多目标拓扑优化的表达式为：

2 汽车零件优化设计

2．1 原零件分析

发动机右上中支架的原始模型如图1所示。材料参数：弹性模量E＝74 GPa，泊松比u＝0．33，弹性极限Re＝160 MPa，要求零件的质量小于680 g，第一阶模态大于650 Hz。

图1 发动机右上中支架原始设计模型

零件计算模型如图2a所示，支架底端采用5个弹簧单元模拟与之接触零件的刚度，弹簧底端固定，零件之间采用螺栓连接，螺栓使用梁单元和刚性单元进行模拟。在X和Z方向，分别受到1 800 N和3 770 N的载荷。对部件进行模态分析和2种工况下的静力学分析。得到原始零件的一阶模态为671．6 Hz，满足设计要求。由于螺栓采用梁单元和刚性单元来模拟，所以在和刚性单元连接的部分会产生相对于其他单元较大的应力，因此，在应力显示的时候，没有考虑凸台以及其他与简化螺栓相连接单元的应力，这样比较真实地反应了零件的应力水平分布。X方向载荷作用下的应力分布如图2c所示，最大应力为41．5 MPa。Z方向载荷作用下的应力分布如图2d所示，最大应力为154 MPa。在试验过程中，零件发生断裂，如图2b所示，可以看到断裂的地方刚好发生在应力过大的地方。由上述分析可知，零件在载荷作用下的应力过大而导致使用过程中的疲劳断裂。再设计过程中，需要考虑零件的刚度要足够大，同时考虑到轻量化设计，零件的体积也要足够小。即需要达到2个刚度最大化和体积最小化这3个目标，所以要用到多目标优化。

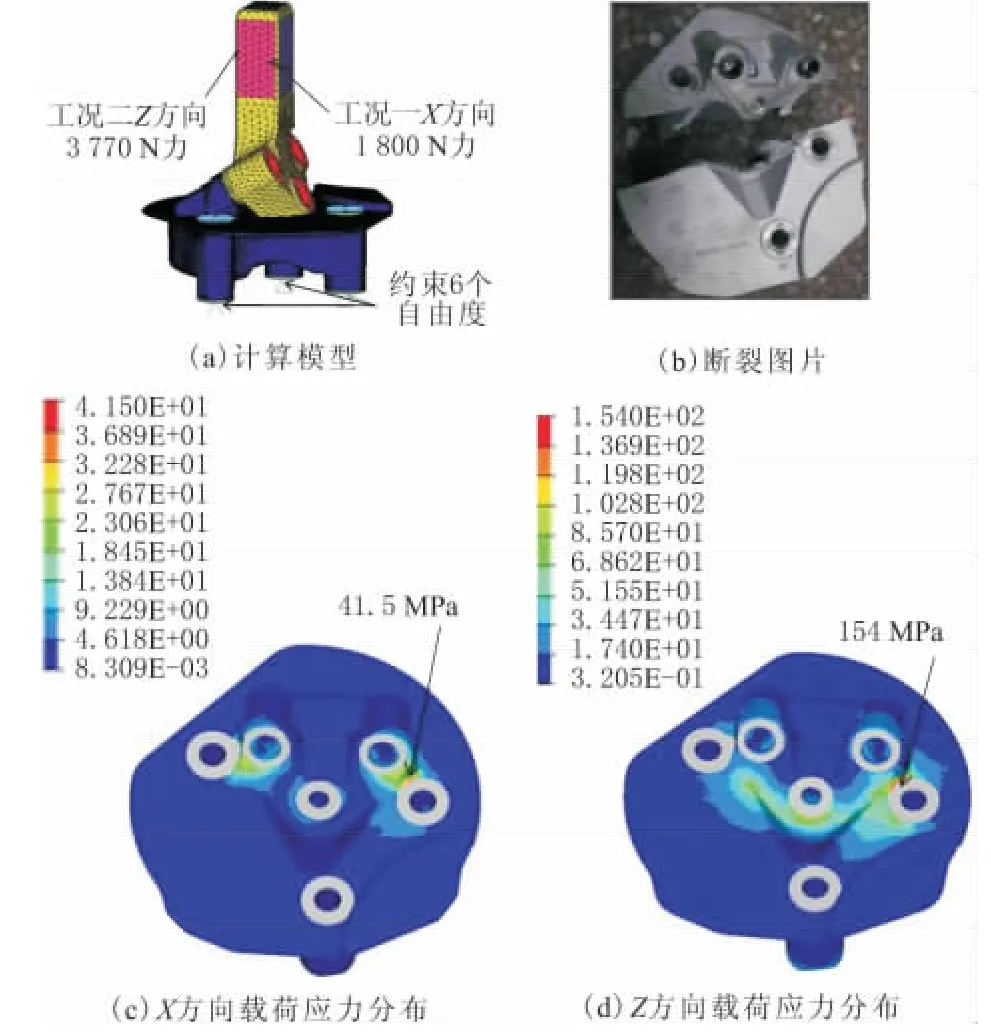
图2 原始设计应力水平分布和断裂图片

2．2 多目标拓扑优化

零件的设计区域和非设计区域如图3a所示。考虑到发动机左上中支架的装配要求，仅对下面的加强筋区域进行拓扑优化。首先将加强筋部分全部填满作为设计区域，优化约束为第一阶模态和体积比。由于设计要求最小一阶模态为650 Hz，零件最大质量为680 g，考虑到误差余量，取最小第一阶模态为660 Hz，体积比最大为0．2。对2种工况分别进行单目标拓扑优化得到各个工况柔度，优化得到的值为这2个目标的期望值。以体积最小化为目标进行单目标拓扑优化，得到体积的期望值和2种工况的柔度。计算得到表2所示的参数。

表2 计算各个工况得到的参数

根据表2选择对角线值为各个目标的理想点，各列最大值为悲观点。根据实际情况中目标允许的最差解，选择伸缩指标。理想点、悲观点和伸缩指标如表3所示。

根据表3数值和式（10）～式（13），使用 Hyper－Math编写目标函数和所需参数的表达式，将Hyper Math函数作为Optistruct进行拓扑优化的外部响应。在迭代过程中零件的材料分布变化如图3所示，材料分布不断得到优化，最终得到如图3c所示的拓扑形状。

表3 选择各个期望值和伸缩指标

图3 迭代过程中材料分布变化

优化过程中规划目标和各个子目标的迭代曲线如图4所示。规划目标和各个子目标都能很快达到收敛，各个子目标都在模糊集内，且有较好满意度。

图4 拓扑优化过程中各个目标的迭代曲线

根据最终优化的拓扑形状（图3c），在Pro／E中重新建模，得到如图5所示的发动机右上支架新设计模型。

图5 发动机右上中支架新模型

2．3 新零件的分析验证

对新零件进行分析，得到第一阶模态为704 Hz，比优化前的增加了32．4 Hz。

通过拓扑优化使得零件的刚度和动态性能都得到了改善，并且减少了零件的质量，拓扑优化前后比较如表4所示。优化后的新零件比原始零件的应力减少了47．1%，质量减少了7．9%

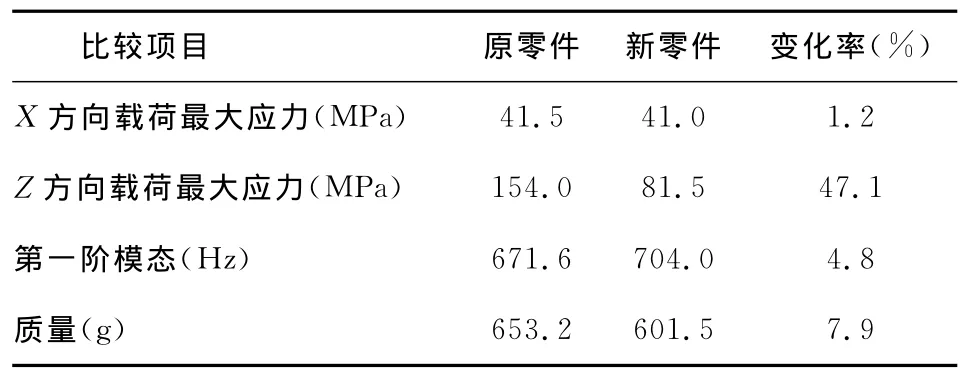
表4 优化前后的比较

3 结束语

模糊理论与加权平方和法结合的基于模糊满意度的变权重多目标规划方法，可以很好地求解多目标优化问题，通过改变权重在计算中优先优化那些远离模糊集的目标，并且使得优化的各个目标的模糊满意度尽量大，使优化后得到的目标值更靠近理想点。另外，通过模糊满意度可以控制优化的各个目标值都在自己期望的范围之内。最后，使用该方法对一个汽车零件结构进行多目标的拓扑优化，使得零件在各个工况下的应力满足要求，应力分布更加均匀，同时提高了零件一阶模态，使得零件具有了更好的动态性能。

［1］ 周克明，李俊峰，李 霞．结构拓扑优化研究方法综述［J］．力学进展，2005，35（1）：69－76．

［2］ 洪清泉，赵 康，张 攀．OptiStruct ＆ HyperStudy理论基础与工程应用［M］．北京：机械工业出版社，2012．

［3］ 朱剑锋，林 逸，陈潇凯，等．汽车变速箱壳体结构拓扑优化设计［J］．吉林大学学报（工学版），2013，42（3）：584－589．

［4］ Kaya N，Karen，ztürk F．Re－design of a failed clutch fork using topology and shape optimization by the response surface method［J］．Materials and Design，2010，31（6）：3008－3014．

［5］ Kilian S，Zander U，Talke F E．Suspension modeling and optimization using finite element analysis［J］．Tribology International，2003，36（4）：317－324．

［6］ 孙晓辉，丁晓红．结构多目标拓扑优化设计［J］．机械设计与研究，2012，28（4）：1－4．

［7］ 范文杰，范子杰，苏瑞意．汽车车架结构多目标拓扑优化方法研究［J］．中国机械工程，2008，19（12）：1505－1508．

［8］ 耿玉磊，张 翔．多目标优化的求解方法与发展［A］．福建省科协第四届学术年会——提升福建制造业竞争力的战略思考专题学术年会论文集［C］．2004．109－112．

［9］ 高济众，吕新生．交互式满意协调法——一种多目标优化方法［J］．合肥工业大学学报（自然科学版），1989，12（2）：32－39．

［10］ Luo Z，Chen L P，Yang J，et al．Fuzzy tolerance multilevel approach for structural topology optimization［J］．Computers and Structures，2006，84（3）：127－140．