一种求解不等式约束凸优化问题的内点方法
2014-07-04吴庆丰
吴庆丰
(淮北师范大学 数学科学学院,安徽 淮北 235000)
不等式约束优化问题是约束优化问题中一类重要问题,一种经典的解法是采用SUMT(sequential un⁃constrained minimization technique)技术,即把约束条件转化为某种惩罚函数加到目标函数中去,从而将约束优化转化为一系列无约束优化问题的求解.本文将采用一种新的内点算法求解,并与传统内点障碍函数法进行比较.下面介绍求解凸优化问题的IPA(inerior point algorithm)方法.
1 IPA算法
文献[1]和文献[2]中分别给出Bregman函数和Bregman-Legendre函数的定义如下:
设S为开凸集,S⊂Rn,对可微函数定义Bregman距离Dg(x,y)=g(x)-g(y)-<∇g(y),x-y>.称g为区域S上的Bregman函数,如果下列条件被满足:
(B1)g于连续且严格凸;
(B2)g于S连续可微;
(B3)Dg(x,·)及Dg(·,y)的水平集有界,
作为对Bregman 函数的扩展,在文献[2]中Bauschke 等引入了Bregman-Legendre 函数的概念.设f:RJ→(-∞,+∞)为适当的闭凸函数,其本质区域定义为这里,我们称凸函数为适当的,如果不存在x使得f(x)=-∞,且存在x满足f(x)<+∞;称适当的凸函数f为闭的,如果f是下半连续的.记Df(·,·):D×intD→[0,+∞),Df(x,z)=f(x)-f(z)-<∇f(z),x-z>,这里 intD表示D的内部,称Df(·,·)为Bregman距离.下面给出求解凸优化问题的IPA方法.
IPA算法[3]给定x0∈intD,对k=0,1,…,求xk+1满足,

这里假定每步迭代中求得的xk+1∈intD.
关于该算法的收敛性,Byrne给出了如下定理.
定理1[3]设存在.如是被唯一确定的,则由如上IPA算法产生的点列{k} 收敛于;如不能被唯一确定,但可在D中选取,则序列{Dh(,k)}和{DF(,xk)}单减.如果进一步,DF水平集有界,则{xk} 有界,且其任一聚点x*∈满足f(x*)=f(x).如h或F为 Bregman-Legendre 函数,本质区域为D,则x*∈D,且点列收敛于x*.
注1:这里DF水平集有界,是指对x∈D及 ∀a>0,集合{z|DF(,z)≤a} 有界.
2 求解不等式约束凸优化问题的内点方法
下面讨论如下不等式约束的凸优化问题的求解:

这里f(x)是Rn中连续可微的凸函数,gi(x),i=1,2,…,m是Rn中连续可微的凹函数.
对于上述问题,一种传统的方法是采用对数障碍函数法求解,即通过求解一系列无约束凸优化问题

来得到(2.1)的解,这里r>0 是罚参数.
记D={x|gi(x)>0,i=1,2,…,m},易知D为开凸集.由于gi(x),i=1,2,…,m是连续可微的凹函数,可知为D上连续可微的凸函数,又由于f(x)为连续可微凸函数,故对r>0,若问题(2.2)存在极小点,则在该点处满足

即对数障碍函数法的每步迭代中,xk+1满足

在对数障碍函数法的计算中,要求罚参数r单减并趋于0,所以当r充分小时,即使严格凸,也可能出现病态问题,使得求解难度增大.那么可否避免这一问题呢?
假设Slater条件成立,即D≠ϕ.由于我们只关心f(x)在D上的取值,不妨假定f(x)在D外的值均为+∞,则f(x)为适当的闭凸函数.令F(x)=f(x)+rh(x),取h(x)使之满足IPA 所要求的条件,基于IPA 可以得到如下算法:
求xk+1∈D使之满足 ∇F(xk+1)=r∇h(xk)或 ∇f(xk+1)+r∇h(xk+1)=r∇h(xk).
令

容易验证h(x)满足IPA所要求的条件.于是,基于IPA可以得到如下算法:
算法1取x0∈D及r>0,对k=0,1,2,…,计算xk+1∈D满足:
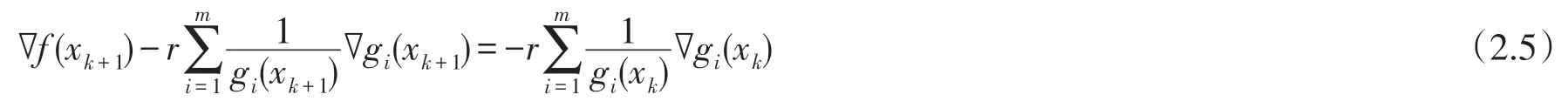
假定每步迭代中满足条件的xk+1存在.

算法1 需要假定每步迭代中xk+1可以在D中求得,也就是当求得的迭代点xk+1∉D时,算法无法实现.下面的关键问题是如何求解(2.5)式,并且保证xk+1∈D.
f(x)和h(x)都是x的凸函数,则F(x)也是x的凸函数.设F(x)是二次可微实函数,给定初始xk∈Rn,Hesse矩阵∇2F(xk)正定.我们在xk附近用二次Taylor展开,

取xk+1=x*,令 ∇F(x*)=0,得xk+1=xk-[∇2F(xk)]-1∇F(xk),此即牛顿法迭代公式.由 IPA 算法可知,∇F(x*)=r∇h(xk),则

由F(x)=f(x)+rh(x)得

此公式与牛顿法公式相似.我们将xk+dk看作(1.1)的一个近似解,这里

令xk+1=xk+dk,如果xk+1∈D,则可以作为下次迭代的初始点.若xk+1∉D,则添加步长αk(0<αk<1),使xk+1=xk+αkdk∈D.显然,当xk+1=xk+dk∈D时直接作为新的迭代点,实际上是默认步长αk=1.
借鉴阻尼牛顿法,加入线搜索技术,搜索准则采用Armijo-Goldstein 准则或Wolfe-Powell准则求步长αk,并且使目标函数值有一定的下降,当xk+1=xk+αkdk∈D时,步长保持不变;当xk+1=xk+αkdk∉D时,减小步长αk直到xk+1=xk+αkdk∈D.在计算搜索方向dk时,增广目标函数的Hesse矩阵仍然有可能奇异或者病态.这时,考虑搜索方向结合最速下降法,即当∇2F(xk)不正定时,令Hesse矩阵为单位矩阵.这时,下降方向为采用最速下降方向.下面给出如下算法.
算法2:
步一 给定终止误差 0≤ε≪1,r> 0,0<c<1,0<η<1,初始点x0∈D,k=1.
步二 若‖∇f(xk)‖≤ε,则x*=xk,算法终止;否则计算搜索方向,记

步三令xk+1=xk+αkdk,若xk+1∈D,k=k+1,转步二;否则缩小步长,令αk=cαk,直 到xk+1=xk+αkdk∈D,k=k+1,转步二.
下降方向dk结合最速下降法时可采用原目标函数负梯度或者增广目标函数的负梯度方向,线搜索可以从原目标函数或者增广目标函数考虑.其实计算的最终目的就是要原目标函数下降,当然又要保证迭代点在可行域内.显然,当迭代点靠近或超出可行域边界时,增广目标函数将趋于无穷大,根据这一点,可通过适当减少步长控制每一步迭代过程中迭代点仍为内点.
上述算法中只需事先给定一个r,不必趋于零,所以避免了传统内点障碍函数法由于rk→0,(k→∞)时,增广目标函数病态问题的出现.线搜索可以从原目标函数或者增广目标函数考虑.从数值实验中计算效果来看,线搜索直接考虑使原目标函数有充分的下降量计算时间更短.其实计算的最终目的就是要原目标函数下降,当然又要保证迭代点在可行域内.这里的内点算法给出了一种新的搜索方向,计算过程中不需要改变r,加入步长控制技术,使迭代点在可行域内部.
3 数值实验
这里给出一个不等式约束的凸优化的例子,采用算法2进行计算.本例的整体极小点容易看出,这样是为了方便与用算法2所计算的结果进行比较.
求解下面优化问题.
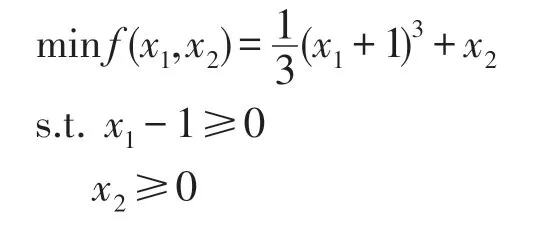
容易看出此问题的整体极小点为x*=(1,0)T.取初始点x0=(2,1)T,这里采用算法2,利用Matlab编程求解,求解结果如表1所示.

表1 算法2求解的数值结果
r的取值不必很小,从数值实验结果看,计算效果还不错.实际上,r如果取得太小,计算中就会导致病态问题的出现,这一点正是传统内点障碍函数法的一个主要缺点.从数值实验中计算效果来看,线搜索直接考虑使原目标函数有充分的下降量计算时间更短.
4 结论
本文提出的内点算法,给出了一种非精确求解IPA的方法,从而便于将算法在计算机上实现,并且还解决了IPA对迭代点在可行域内部的假定.算法中只需事先给定一个r,不必趋于零,所以避免了传统内点障碍函数法由于rk→0,(k→∞)时,增广目标函数病态问题的出现.这里的内点算法给出了一种新的搜索方向,计算过程中不需要改变r,加入步长控制技术,使迭代点在可行域内部.关于算法的收敛性证明将是另一重要内容.
[1]BREGMAN L M.The relaxation method of finding the common point of convex sets and its application to the solution of problems in convex programming[J].USSR Computational Mathematics and Mathematical Physics,1967,7(3):200-217.
[2]BAUSCHKE H H,BORWEIN J M.Legendre functions and the method of random Bregman projections[J].Journal of Con⁃vex Analysis,1997,4(1):27-67.
[3]BYRNE C.Block-iterative interior point optimization methods for image reconstruction from limited data[J].Inverse Prob⁃lems,2000,16(5):1405-1419.
