二维晶格色散关系和态密度的紧束缚模型计算

王妮娜，路洪艳，魏梦俊，徐慧，刘晓静，张娇娇，胡新春

（淮北师范大学 物理与电子信息学院，安徽 淮北 235000）

利用紧束缚模型计算晶体的色散关系比较简单，既易于计算、又便于理解，对理解不同晶格的电学性质提供理论基础.随着计算机科技的高速发展，将理论计算结果与计算机软件结合起来，能将结果可视化，图形化，便于建立清晰的物理图像.因此，本文拟采用紧束缚模型计算二维正方、三角、六角格子晶体的电子色散关系，并进一步计算相应的态密度，为理解这3种晶格的电学性质提供一定的理论基础.

1 紧束缚模型求正方、三角格子色散关系和态密度

如果考虑到电子在最近邻和次近邻格点的跳跃，相应的紧束缚模型哈密顿量为

式中，i为晶格上的格点，δ和δ′分别代表最近邻和次近邻的键，Ci和分别代表在i格点电子的湮灭和产生算符，h.c代表复共轭，t和t′分别代表电子在最近邻和次近邻上的跳跃积分能量，μ代表化学势.做傅里叶变换

可得紧束缚模型的哈密顿量为：

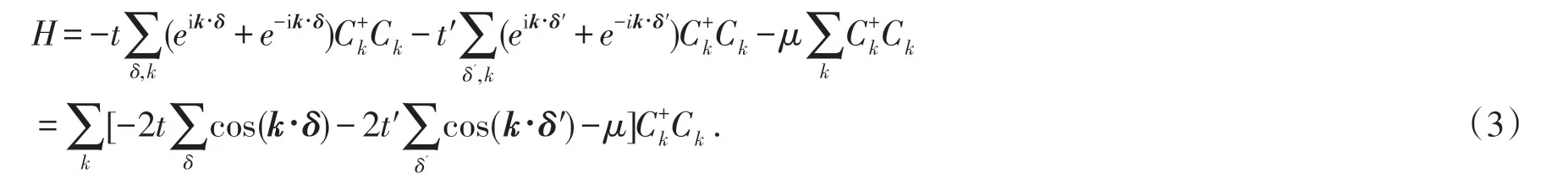
可知，色散关系为：

本文中令最近邻格点之间的距离a=1，对于正方格子，δ的坐标为（0，±1）和（±1，0），δ′的坐标为（±1，±1），同时考虑到正方格子原胞中每个键为两个原胞所共用，所以正方格子的色散关系为：

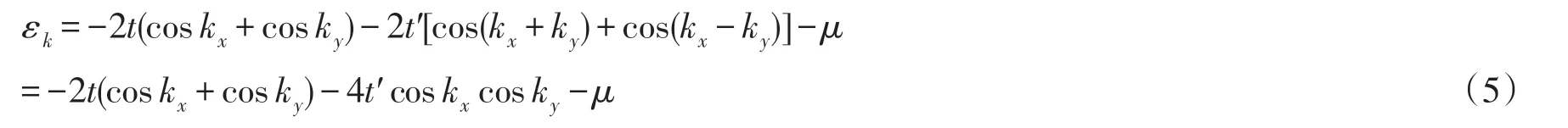
式中的kx，ky是k在（x，y）上的分量，若只考虑电子在最近邻格点上的跳跃，则t′=0.设μ=0，则正方格子的色散关系变为：

可以用Matlab软件［1］将正方格子色散关系表达式进行图形化，结果如图1a所示.

态密度表达式为：

式中k为第一布里渊区中的点，η为无穷小量，计算时取η=0.01.用Fortran 软件［2］编程计算对应的态密度，计算结果可以用Origin软件画图，结果如图1b所示.

图1 正方格子的色散关系

由图1a可知，色散关系图是关于k=0 对称，但关于E=0不对称，能带对应能量的取值范围[-4t，4t]，带宽为8t.图1b 为态密度曲线，态密度的峰值在E=0 处，这个峰称为范霍夫奇异峰，态密度图关于E=0对称.

对于三角格子，δ的坐标为（±1，0）和δ′的坐标为借助（4）式可计算出三角格子的色散关系为

如果只考虑电子在最近邻格点上的跳跃，则三角格子的色散关系为：

用Matlab软件将三角格子的色散关系表达式进行图形化，结果如图2a所示.

同样可以利用（7）式计算三角格子的态密度，然后用Fortran软件进行编程计算，最后用Origin作图，结果如图2b所示.

图2 三角格子的色散关系

由图2a可知，色散关系图是关于k=0 对称，但关于E=0不对称，能带对应的能量取值范围是［-6 t，3 t］，带宽为9 t.图2b为态密度曲线，态密度的峰值在E=2 t处，这个峰也是范霍夫奇异峰，且态密度图不关于E=0对称.

2 紧束缚模型求解六角格子的色散关系和态密度

对于六角格子，现以石墨烯为例.石墨烯（Graphene）是由碳原子以sp2杂化形成的二维六角蜂窝状结构［3］，理论上认为石墨烯不可能二维存在.2004年，英国曼彻斯特大学的Geim首先用微机械剥离法制备出了石墨烯［4］，并于2010年获得诺贝尔物理学奖，引起人们的广泛关注.不再像前面所讲的正方、三角格子是简单格子，六角格子是由A、B两套子格套构而成的复式格子.对应的紧束缚模型哈密顿量为：

式中，i和j分别代表六角格子中最近邻和次近邻的格点，ai和分别代表在a子格i格点电子的湮灭和产生算符，bj和分别代表在b子格j格点电子的湮灭和产生算符.做傅里叶变换，可得紧束缚模型的哈密顿量为：

可令上式中

对于六角格子，上式中δ的坐标为（0，-1）和则：

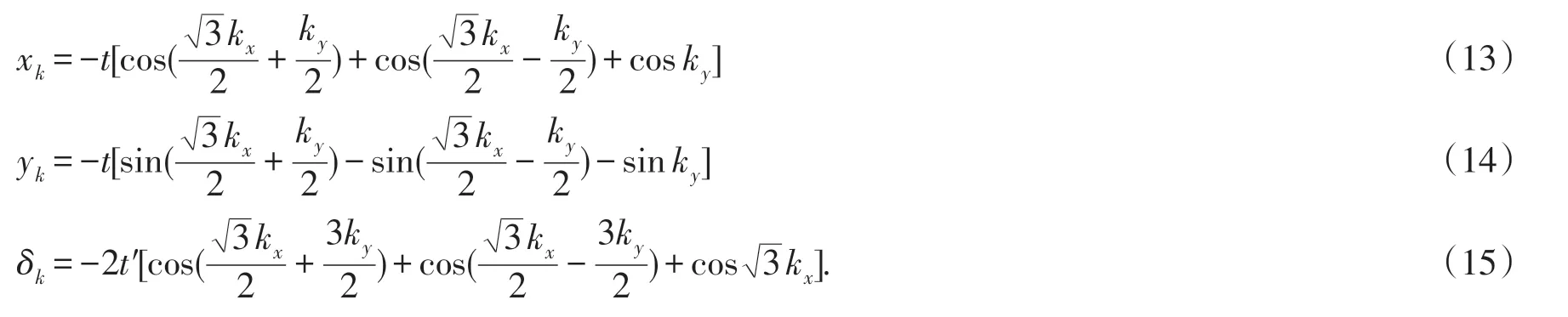
按照（12）式替换后，哈密顿量（11）式可以化简成：

可以进一步写成矩阵形式，即

色散关系可通过下式得到：

求行列式，可得

把（13）-（15）式带入（19）式可得六角格子的色散关系为

若只考虑电子在最近邻格点上的跳跃，色散关系为：

以上结果是从二次量子化后的哈密顿量得到的，与从波函数角度出发理论计算的结果［5］一致.若同时考虑电子在次近邻格点上的跳跃，则（20）式中的t′=0.2t［6］.同时，我们在计算中都设μ=0.

用Matlab软件将六角格子的色散关系表达式进行图形化，只考虑电子在最近邻格点上的跳跃和考虑到电子在次近邻格点上的跳跃的色散关系结果分别如图3a和3b所示.

六角格子的态密度表达式为：

式（22）中ε1和ε2分别对应于（20）式中εk取正号和负号的值，按照（22）式，用Fortran软件编程计算对应的态密度，然后用Origin作图，结果如图3c和图3d所示.

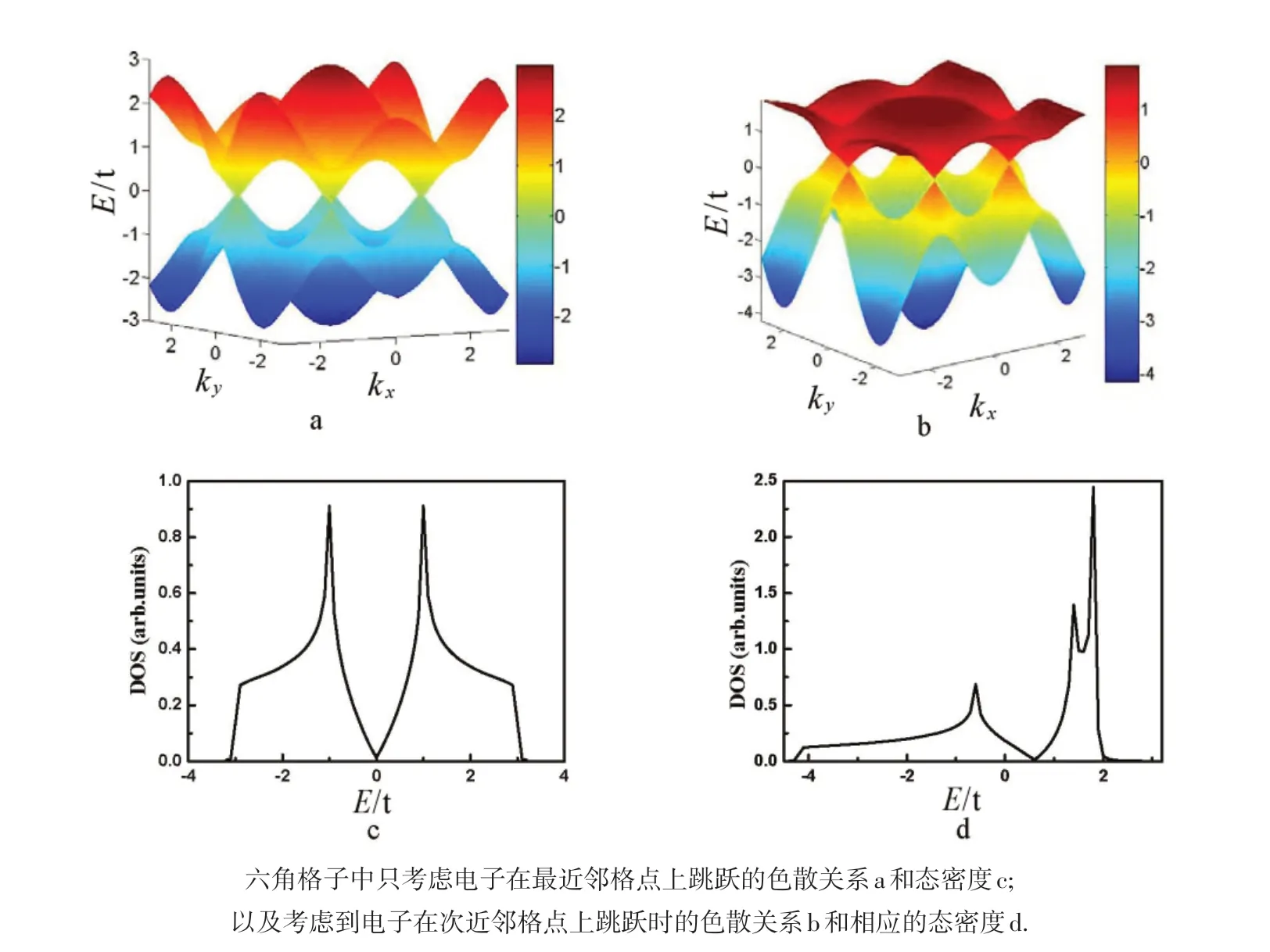
图3 六角格子的色散关系

由图3a可知，只考虑电子在最近邻格点上跳跃，上、下两带是对称的，相交于第一布里渊区的6个顶点，也被称为Dirac点.Dirac点附近能带具有线性色散关系.能带对应能量的取值范围为［-3 t，3 t］，带宽为6 t.费米面刚好处于价带和导带相交的顶点处，可知，石墨烯是带隙为零的半导体.由图3c可以看出，在Dirac点附近，态密度具有线性关系，而且态密度关于E=0对称.如果考虑到电子在次近邻格点上的跳跃，由图3b可知，上、下两带是不对称的，这是因为电子-空穴对称性被破坏.能带对应能量的取值范围为［-4.2 t，1.85 t］，带宽为6.05 t.由图3d可以看出，价带和导带的态密度也不再关于Dirac 点对称.这些结果与文献中的一致［7，8］.

3 结论

本文详细介绍了利用紧束缚模型求解二维正方、三角、六角格子的色散关系和态密度.然后根据色散关系和态密度的表达式，用Matlab 软件并借助Fortran 软件编程，作出了色散关系图和态密度图，可以更容易建立清晰的物理图像.对结果进行了分析和讨论，这些结果对理解不同晶格的电学性质提供了理论基础.

［1］王永龙，张兆忠，张桂红.MATLAB 语言基础与应用［M］.北京：电子工业出版社，2010:70-79.

［2］谭浩强，田淑清.FORTRAN 语言［M］.北京：清华大学出版社，1981:25-40.

［3］KOTOV V N，UCHOA B，PEREIRA V M，et al.Electron-electron interactions in graphene：Current status and perspectives［J］.Reviews of Modern Physics，2012，84（3）：1068-1070.

［4］NOVOSELOV K S，GEIM A K，MOROZOV S V，et al.Electric field effect in atomically thin carbon films［J］.Science，2004，306：666-669.

［5］梁先庆.石墨烯能带结构的紧束缚近似计算［J］.广西物理，2011，32（1）：7-10.

［6］NETO A H C，GUINEA F，PERES N M R，et al.The electronic properties of graphene［J］.Reviews of Modern Physics，2009，81（1）：110-114.

［7］LU Hongyan，CHEN San，XU Yuehua，et al.Electronic Raman spectra in superconducting graphene：A probe of the pairing symmetry［J］.Physical Review B，2013，88（8）：085416.

［8］LU Hongyan，WANG Qianghua.Electronic Raman scattering in graphene［J］.Chinese Physics Letters，2008，25（10）：3746-3749.