分析负反馈放大电路的等效解析法
2014-07-04张知群
张知群
(中国海洋大学信息科学与工程学院山东青岛,266100)
我们可以用传统的四种反馈类型来描述负反馈放大电路[1]。本文介绍的等效解析法可把所有的负反馈放大电路归结为同一个母体等效电路来硏究,並从中定义一组结构参数AoLFoL,用电路分析法来解析电路。
1 母体等效电路和三种输入方式
用分立件组成的外部无反馈的放大电路都能归结为和运算放大器一样的等效电路图1。A0和A0L是不接和接负载电阻RL时受控源的电压增益,其中


图1 外部无反馈的放大电路
图2的电路在无输入时,即是所有负反馈放大电路的母体等效电路。其负反馈的结构性判据是,反馈电阻RF桥接在输出和反相输入点之间。母体等效电路本身就是个负反馈系统。它有三种可用的输入方式:①反相输入;②同相输入;③桥上输入。以前无人注意到桥上输入,本文将证明它是一种新颖的电压跟随器。

图2 负反馈放大等效电路的三种输入方式
2 节点方程组解读出的A0L和F0L
我们可以写出图2的节点方程组为

上式等号右侧是三个垂直竖列①、②和③,是由上述三种输入方式的输入源形成的。它们与等号左侧的电导行列式构成三种输入方式下的节点电位方程组。
当把方程组等号左侧的电导行列式计算出来并写成 c[1+AF]的形式时,可以发现[1+AF]是:

显然,A0L就是真正的开环增益,与A0L相乘的因子则应是负反馈系数F0L。此时,把图2(b)所示的母体电路受控源用输入电压V'0代替,则在净输入处就会产生反馈电压从分压比即可算出
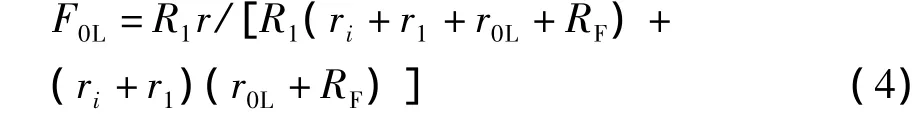
以上定义的唯一的一组结构参数A0L和F0L,不仅与输入和输出无关,而且也易于计算和测量,既能反映母体电路固有的结构特征,又揭示了受控源是负反馈的动力源。
3 闭环增益定理
本文中定义:①增益和闭环增益是指电路中节点电位或支路电流与输入信号电压或电流之比;②零受控状态是指受控电压源短路、受控电流源开路的状态,在这个状态下的增益、输入或输出电阻称为零受控增益AZC或零受控输入或输出电阻;③接近因子Near能反映闭环增益接近理想增益的程度。其定义为

3.1 闭环增益定理
可以证明,对于图2所示的负反馈放大电路,不论是哪种输入方式,各节点电位及各支路电流的闭环增益AF,与相应的零受控增益AZC、理想增益Aid、反馈深度D=(1+A0LF0L)和接近因子Near,都可以用一个通式表示出来,即
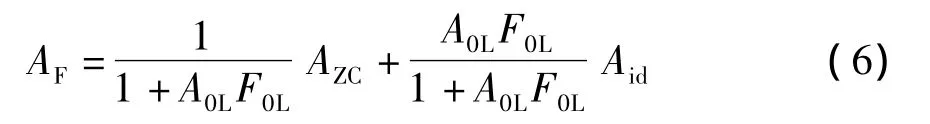
这就是闭环增益定理。为说明详情,可把它改写为叠加原理的形式:

从上式可知:AZC是输入通过RF的传输作用所产生的;后项是受控源所产生的,-AZCNear是受控源通过RF所产生的的反馈项,其略小于AZC而使AZC削弱D倍,而NearAid是受控源产生的近理想增益。
可见,闭环增益的完全解由两项组成:①闭环零受控增益,等于zZC被削弱了D倍;②近理想增益,等于理想增益Aid乘以接近因子Near。当然,这些闭环增益中,有的含有这两项,有的却只有其中的一项。
3.2 闭环增益定理的证明
从方程组(3)来看,任何节点电位的闭环增益都等于两个行列式之比。式中分母都是含有因子[1+A0LF0L]的电导行列式;而分子行列式中必有一列是垂直竖列①,②或③。当垂直竖列中的独立电流源与它的余因式相乘时,可能产生不含因子A0L的项和含因子A0L的项。因此,节点电位的闭环增益的形式应是
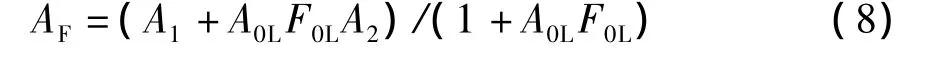
其中,A1和A2待定。当A0L=0时,即零受控时,AF=A1=AZC;而当A0LF0L≫1时,即深度负反馈时有AF=A2=Aid。由此就证明了上式就是节点电位的闭环增益的通式(6)。
由于支路电流的闭环增益等于两个节点电位之差除以支路电阻,证明了式(6)也是它们的通式。
4 闭环增益实用定理
从闭环增益定理通式(6)看出,对于那些Aid≠0的闭环增益而言,当它们的理想增益和零受控增益为同量级时,近理想增益比闭环零受控增益大了约A0LF0L倍,所以实用上可只取近理想增益为其闭环增益,即

这就是闭环增益实用定理。
我们略去闭环零受控增益,实质上是黙认了准虚短是成立的:即(Vp-Vn)→0,且Iri→0(比虚短Vp-Vn=0且Iri=0的说法更確切)。这样,利用准虚短求出的理想增益和电路的接近因子相乘就可直接写出如图2(a)所示的反相输入、同相输入和桥上输入之下的恒压和恒流输出。

从式(10)~(14)来看,V0与 RL无明显关系,RL的改变仅对Near有很小的影响。可见,不管是何种输入方式,输出电压V0都有很好的稳压特性。
从式(11)~(15)来看,Ir0与r0无明显关系。如果把负载R!L与r0串联,则(r0+RL)的改变仅对Near有很小的影响。可见,不管是何种输入方式,受控源支路电流都有很好的稳流特性。
另外,从式(14)可知,桥上悬浮输入是一种新颖的电压跟随器,由于反馈环能对伩号源两极的共模干扰有削弱作用,所从它很适用于某些传感电路的输入级。
5 三个闭环输入电阻和二个输出电阻
用电路分析法求输入电阻和输出电阻较为麻烦,考虑到Aid=0时的V=D-1VZC或 I=D-1IZC,求解就特别简单[2,3]。
5.1 同相输入处的输入电阻
零受控输入电流与零受控输入电阻的关系是

由于闭环输入电流也是净输入电流Ir1=Iri=D-1IriZC,所以图2②所示的同相输入处的闭环输入电阻是

这说明,同相输入处的闭环输入电阻相当于把其零受控输入电阻[ri+r1+R1‖(RF+r0L)]提高了D倍。
5.2 桥上输入处的输入电阻
零受控输入电流与零受控输入电阻的关系是

因反相输入点n构成准虚地,闭环输入电流IRF的理想增益为零,IRF=D-1IRFZC。所以,图2③所示的桥上输入处的闭环输出电阻是

这说明,桥上输入处的闭环输入电阻相当于把其零受控输入电阻提高了D倍。
5.3 反相输入处的输入电阻
因IR1包含有近理想增益,所以此时要另找方法。我们可先求Vn,再求IR1和这个输入电阻。根据弥尔曼定理,此时反相输入点n的零受控电位是
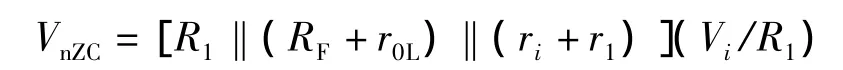
因为n点构成准虚地,它的闭环电位应是Vn=D-1VnZC,则有
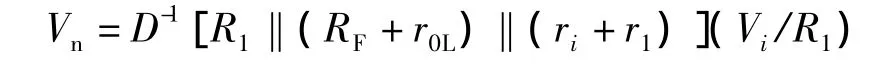
可见,图2①所示的反相输入处的输入电阻应该是
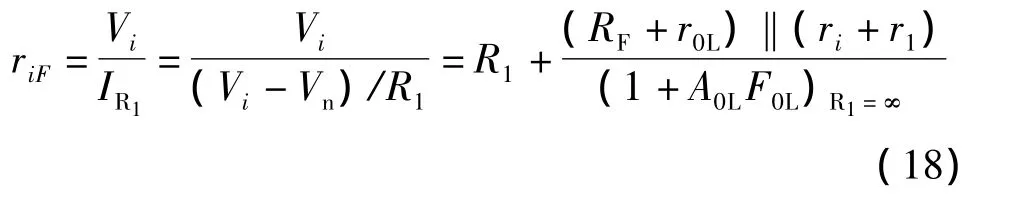
这说明,反相输入处的闭环输入电阻由两项组成:第一项R1不因负反馈而改变;第二项是从反相输入点n看进去的闭环输入电阻,它等于把这里的零受控输入电阻降低了(1+A0LF0L)R1=∞倍。在深度负馈之下,反向输入的闭环输入电阻趋于R1。所以,对于RC耦合的反向输入的负反馈放大器,並不能展宽低频端的带宽,传统的推论是不正確的。
5.4 穏压输出处的输出电阻
用准虚短可以证明,图3和图4这种组态电路的所有的理想增益都为零,而AF=D-1AZC。

图3 求恒压处输出电阻 图4求恒流处输出电阻
图3输出处的零受控输出电压与零受控输出电阻的关系是
VOZC=I{ro‖[RF+R1‖(ri+r1)]},而闭环输出电压VO=VOZC/(1+AOFO),所以穏压输出处的闭环输出电阻是
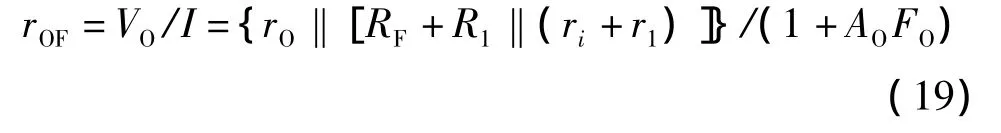
上式表明,负反馈使得Vo处的闭环输出电阻只是零受控下的输出电阻rO‖[RF+R1‖(ri+r1)]的(1+A0F0)分之一。在深度负反馈之下,這一输出电阻趋于零,所以是恒压源。
5.5 穏流支路断开处的输出电阻
图4所示的穏流支路的零受控输入电流与零受控输入电阻的关系是
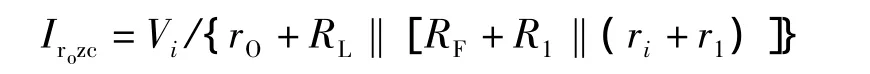
而闭环输入电流IrO=D-1IrOZC,所以穏流支路断开处的闭环输出电阻是

可见,受控源支路断开处的输出电阻等于把零受控的闭环输出电阻rO+RL‖[RF+R1‖(ri+r1)]增大了D倍。显然,受控源支路在三种输入方式之下都具有穏流特性。
6 负反馈放大电路实例计算
[例1]图5(a)是由一只晶体三极管组成的负反馈电路,试计算它的 AFO=VO/Vi,riF和 rOF。
已知:R1=10kΩ,RF=40kΩ,RC=RL=5kΩ,rbc=1kΩ,β =50。
解:断开RF后可求得A0=βRC/rbe=250,A0L=β(RC‖RL)/rbe=125,ri=rbe=1kΩ。由此可得到图5(b)的等效电路。由式(4)和式(19)可求得F0L=0.0209,AOLFOL=2.613,(1+A0LF0L)R1=∞=3.875,D=3.613,Near=0.723。

图5 单管反相输入负反馈放大电路
由闭环输入电阻式(18)及闭环输出电阻式(19)得:riF=10.252kΩ,rOF=1.282kΩ。由式(3)解出的闭环输出电压增益的全解式可得
AFO=D-1[F0Lr0L(ri+r1)/R1ri]+Near(-RF/R1)=0.0015+(-2.892)
可见,即使反馈深度不大,也可略去第一项,从而验证了闭环增益实用定理的实用性。
[例2]图6(a)是μA741组成的运算电路,其参数是:A0≥50000,ri≤500kΩ,ro≫0.2kΩ。试计算负载RL=1.8kΩ之下,集成运放参数不理想会造成的误差。
解:由图6(b)等效电路可得,RL=1.8kΩ时有:
A0L≥45000,FOL=0.08760,AOLFOL=3942,Near=0.9997,AFO=-9.997。
可见,按理想运放计算所产生的误差小于(10-9.997)/10=0.03% 。
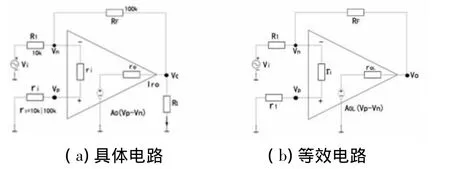
图6 用μA741接成的反相比例运算电路
下面,我们来求证接近准虚短的程度。如果输入信号Vi=1V,则有
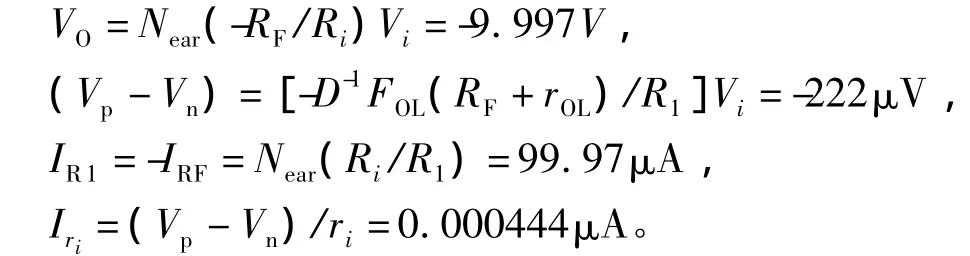
从上面四个数据的比较来看,“准虚短”的条件是滿足的。
7 等效解析法与传统分析法比较
7.1 不同的起点
传统分析法忽视了电路中电压和电流之间的相互依存和相互制约的关系,从而把输入方式与输出电压和电流一起搭配成四种反馈类型,使分析有些复杂化了。
等效解析法把母体电路的结构特征(內因)看成是变化的根据,把不同的输入(外因)看成是变化的条件,把由此产生的具有共性、个性的闭环响应和闭环输入、输出电阻,看成是必然呈现的规律。
7.2 不同的方法得出不同的內涵
传统法是用框图引入四种闭环输出公式,从具体电路中剝离出四种基本放大电路和反馈网络。四种闭环输出公式及有关的闭环输入和输出电阻,都是以基本放大电路和反馈网络作为参考来讨论的。
本文的等效解析法是用电路分析的方法去分析母体电路在三种可用输入之下的响应。从节点方程组(3)的电导行列式中解读出唯一的一套与输入、输出无关的结构参数AOL和FOL,并从解出所有的闭环电压和电流增益中总结和证明了等效解析法的核心结论—闭环增益定理式(6)。
对于Aid=0的那些闭环增益,从闭环增益定理推证出更简单的闭环增益实用公式。对于Aid=0的那些闭环增益AF=D-1AZC,推证出求解闭环输入电阻和输出电阻的简易方法。
等效解析法导出的闭环特性,直接与电路本身的特定状态(零受控和理想状态)以及电路特性参数(反馈深度和接近因子)有关。
7.3 闭环增益实用公式和传统增益公式
式(9)所示的闭环增益实用公式AF=A0LF0L·Aid/(1+A0LF0L)和传统的增益公式AF=A/(1+AF)都是在忽略了信号源通过RF的传输作用条件下导出的,所以具有可比性。
两式非常类似,差别只是多了常数F0LAid。所以等效解析法也能象传统分析法那样去证明稳定性和频带展宽等那些正確的结论。
两个表述式代表的功能相差很大:传统的四种类型的闭环输出公式,仅用于讨论负反馈电路的输出特性;而闭环增益实用公式,可比较確切地求出电路在三种输入下的各节点电位及各支路电流的闭环增益。
8 结语
本文介绍的等效解析法采用新思路和新方法,形成了比较完备的分析方法。由此分析方法得出的结论,不仅能覆盖传统方法得出的全部正確的结论,而且还有所创新。这种更加理性化的分析方法,可以深化我们对负反馈放大电路的认识。
[1]王成华,电子线路基础[M].北京:清华大学出版社,2008.11
[2]张知群,关于负反馈放大器的一种新的分析方法的探讨[J].济南:山东电子,1985年第2期
[3]张知群,负反馈放大电路的等效解析法分析[J].南京;电气电子教学学报,2010﹙6)-34
