矢量叉积运算满足分配率的一种简单证明

焦重庆

(华北电力大学电气与电子工程学院，北京102206)

0 引言

矢量分析与场论是学习“电磁场”课程的基本数学工具。在矢量分析中，叉积运算则是两个矢量之间的基本运算之一。叉积教学时，一般要先讲其几何定义:

其中，A、B为矢量，A、B分别为其模。θ为A、B之间的夹角。en是与A、B都垂直的单位矢量，且A、B、en三者呈右手螺旋关系。

然后，介绍叉积在直角坐标系下的计算公式:

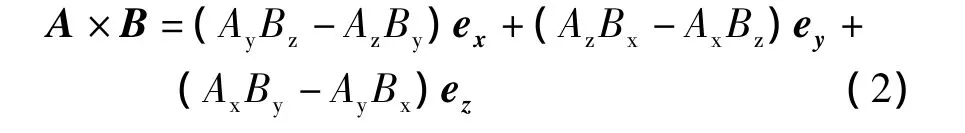
式中，ex，ey和ez分别为x，y和z方向的单位矢量。

从式(1)到式(2)，其关键是承认叉积运算满足分配率，即

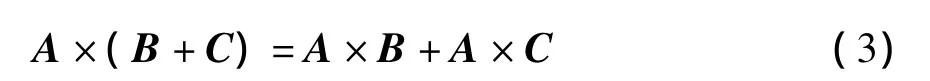
上式根据式(1)给出的几何定义，并根据以下六个等式直接导出:

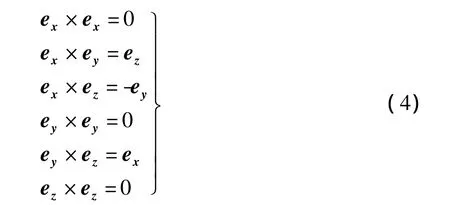
在电磁场教材中，一般对叉积运算的分配率性质没有给出证明[1-4]。实际上，这一性质的得出并非显而易见，由于涉及到方向的旋转问题，具有一定的难度，特别是对于初学的本科生。在美国麻省理工学院教材中，特意在附录部分用约1页的篇幅，对这一性质进行了证明，但过程稍显复杂[5]。

本文则借助于矢量之间的标量三重积等式，给出了叉积运算满足分配率的一种非常简单的证明。

1 标量三重积

矢量A、B、C之间的标量三重积定义为A·(B×C)，它满足如下等式

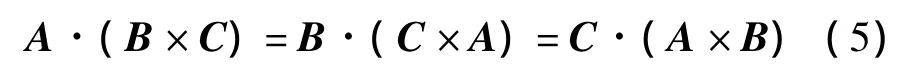
上式证明见图1。A·(B×C)代表了图1中平行六面体的体积，同理，B·(C×A)和C·(A×B)均代表了该平行六面体的体积。不难理解，式(5)的得出并不需要用到叉积运算满足分配率性质。

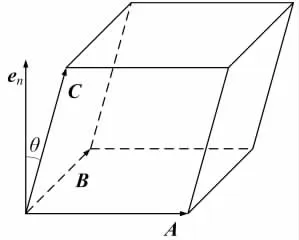
图1 标量三重积的几何意义示意图

2 叉积运算满足分配率的证明

借助式(5)，有

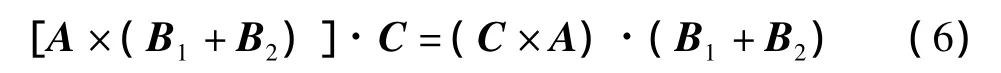
由于点积运算满足分配率，进而从上式可得:

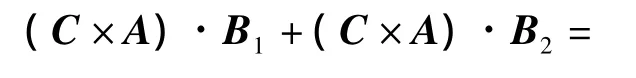
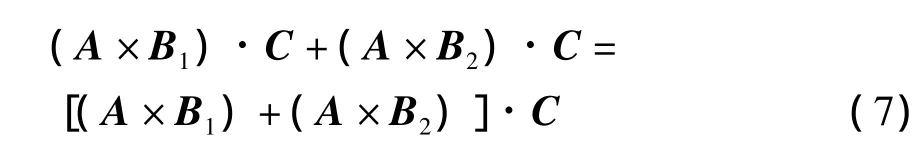
上式第二步的导出用到了式(5)。综合式(6)和式(7)，有

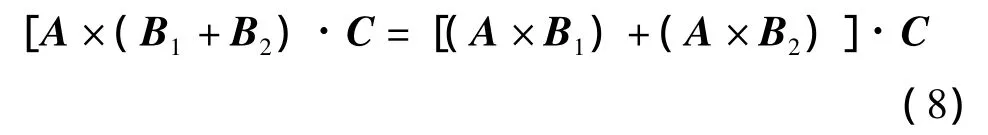
由于C的任意性。从式(8)导出

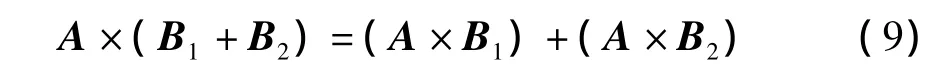
叉积运算满足分配率由此得证。

3 结语

矢量之间的叉积运算满足分配率是推导直角坐标系下叉积计算公式的基础。叉积运算满足分配率的证明过程在一般电磁场教材中很少涉及。本文提出了一种证明叉积运算满足分配率的方法，该方法基于矢量之间标量三重积的循环等式，具有思路新颖且简单易懂的特点，对电磁场理论部分教学有参考意义。其中，标量三重积的循环等式的证明依据了平行六面体的体积公式，属于一般电磁场教材上的常规内容，几何意义明确且便于学生理解和接受。

[1]倪光正.工程电磁场原理[M].北京:高等教育出版社，2009.

[2]冯慈璋，马西奎.工程电磁场导论[M].北京:高等教育出版社，2000.

[3]王泽忠，全玉生，卢斌先.工程电磁场[M].北京:清华大学出版社，2011.

[4]雷银照.电磁场[M].北京:高等教育出版社，2008.

[5]Markus Zahn.Electromagnetic Field Theory:A Problem Solving Approach[M].Krieger Pub Co，2003.