关于电容电压和电感电流跃变的讨论
2014-07-04田社平
田社平,孙 盾,张 峰
(1.上海交通大学电子信息与电气工程学院,上海200240;2浙江大学电气工程学院,浙江杭州310027)
0 引言
由电路中电容、电感元件的电压—电流关系可知,如果冲激电流流过电容,则电容电压是可以跃变的;如果冲激电压出现于电感的两端,电感电流也是可以跃变的。在“电路分析”课程和“电路理论”课程的教学中,往往将电容电压和电感电流的跃变作为教学内容之一。
一个动态电路,在什么样的情况下会出现电容电压和电感电流的跃变呢?一般的观点认为有两种情况可能会出现冲激电压和冲激电流:①外施电源本身就是冲激电源;②外施电源并非冲激电源时,而电路中存在纯电容和(或无)电压源构成的回路或存在纯电感和(或无)电流源构成的割集[1]。
笔者在教学时,学生常常提出这样的问题:除去上述两种情况,是否存在其它引起电容电压和电感电流跃变的电路?问题的答案是肯定的。下面就结合笔者的教学实际对此进行讨论。
1 引起电路参数改变的实例
1.1 电感电流改变例一
图1为一个含全耦合电感的电路。图1(a)中,已知i1(0-)=i2(0-)=0A。图1(b)为该电路的s域模型。我们可采用拉普拉斯变换方法来求电路中的i1和i2。

图1 一个含全耦合电感的电路
我们采用网孔法列写图1(b)电路的电路方程,可以得到

由上式求得

对上式求拉普拉斯逆变换,得到时域解为

由上式看出:i1(0+)=0.5A,i2(0+)=-0.5A,说明电流i1、i2在换路时都有跃变。如果简单地认为耦合电感的原边是一个电感,因它与电阻串联,就会得出电感电流连续,即i1(0+)=i1(0-)=0A的结论,从而与式(3)的结论矛盾。
图1(a)电路中,既不存在冲激电源,也不存在纯电感和(或无)电流源构成的割集,这说明一般认为可能会出现冲激电流、冲激电压的两种情况并未包括全部。
值得指出的是,在外电源上没有冲激源的情况下,图1(a)电路电感电流产生突变的原因是由于自感产生的冲激电压被互感冲激电压抵销了的缘故,这也说明有电感时的电感与独立电感是不同的。
1.2 电感电流跃变例二
图2是另一种出现电感电流跃变的电路例子。这里假设uC(0-)=10V,iL(0-)=0A。初看电路,可能认为电路包含RLC串联支路,电路不可能出现电容电压和电感电流的跃变。事实并非如此,下面采用时域方法加以分析。

图2 含串联RLC的电路
列写t≥0时的电路方程为

由式(4)可知,尽管图2电路包含LC两个动态元件,但其电路方程却是一阶的,因此图2电路是一个退化了的一阶电路。
由初始条件uC(0-)=10V和式(4)中的第一式即可解得电容电压为

进一步,得到

由上式可知,iL(0+)=-30A≠iL(0-)=0A。这说明电路中电感电流发生了跃变,即电感两端出现了冲激电压。图2电路也可采用拉氏变换分析,结果相同。
值得指出的是,图2电路中尽管包含LC两个动态元件,但电路中仅出现冲激电压,而不出现冲激电流,这是由电路拓扑结构所决定的。对于图2电路,如果回路中电感两端出现冲激电压,由于受控电流源两端的电压为任意值,并不违反KVL定律。
如图3所示,该电路是图2电路的对偶电路。通过分析不难发现,电路中存在冲激电流而不存在冲激电压。这里不再赘述。
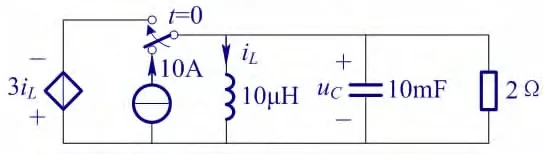
图3 与图2电路的对偶电路
2 进一步的讨论
2.1 与换路定律的关系
在实际电路中,如果包含电容或电感元件,则这两种元件不消耗能量,只是存储能量并与外电路交换能量。当电路换路时,电容或电感从外电路吸取能量或向外电路释放能量都必须经过一段时间才能完成。否则,这就意味着电容、电感所存储的能量发生跃变,那么能量交换的速率(即功率)将为无穷大,这在实际情况下是不可能的[2,3]。
假设电容C两端的电压为uC,流经电感L的电流为iL,则电容存储的能量为Cu2C/2,电感存储的能力Li2L/2。它们吸收的功率分别为CuC(duC/dt)和LiL(duC/dt)。假设换路发生在t=0时刻,由于能量不能发生跃变,因此在换路瞬间,电容两端的电压和

上式所表达的内容亦称为换路定律。
显然,电容电压和电感电流的跃变是违反换路定律的。这说明应用换路定律是有条件的,即必须保证电路在换路瞬间电容电流、电感电压为有限值。
在教学实践中,时常有学生提出这样的困惑:既然有换路定律成立,为何又有违反换路定律的电容电压和电感电流跃变呢?笔者认为应该处理好两者之间的关系:针对实际电路,换路定律成立,它是一个普适的定律;而电路模型是对实际电路的理想抽象化,在电路模型中允许违反换路定律的情况存在。从这一点而言,换路定律和电容电压和电感电流的跃变提供了一个廓清(实际)电路和电路模型之间区别与联系的生动而具体的例子。
2.2 对电路分析的作用
电容电压和电感电流的跃变是电路理论中的一个客观存在,利用它能帮助我们更方便地分析实际的电路。下面举例加以说明。
图4为电工电子技术中常遇到的补偿分压器。其中电容C2为输出端的等效电容,C1为有意加入的补偿电容。现在要求补偿电容C1取何值为合适?图4(a)电路是一个二阶电路,分析较为复杂。电感中的电流应该保持不变,而不会发生跃变
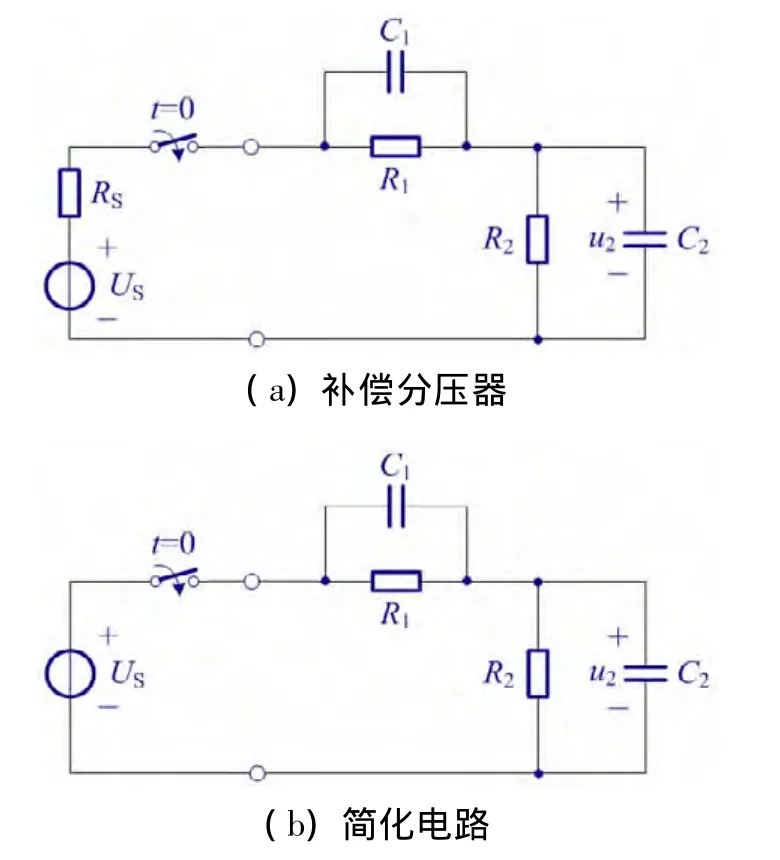
图4 补偿分压器电路
考虑到直流电源的内阻RS一般较小,可将图4(a)电路简化为图4(b)电路。对图4(b)电路进行分析要比图4(a)电路分析简单得多。我们运用三要素法,不难得出有
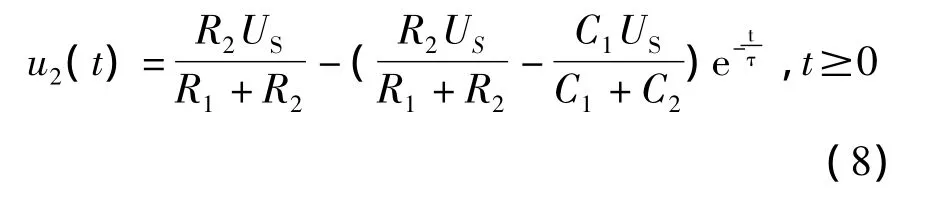
式中,τ=R1R2/(R1+R2)(C1+C2)。由上式可以看出,补偿电容 C1应满足 R2US/(R1+R2)=C1US/(C1+C2),亦即R1C1=R2C2。当调节C1使之满足R1C1=R2C2,则分压器表现如同一个纯电阻分压器。
值得注意的是,由于图4(b)电路中存在纯电容和电压源构成的回路,因此电容中出现了冲激电流。而在图4(a)电路中则不存在冲激电流。出现这种矛盾情况是由于图4(b)电路过于理想化的缘故。尽管如此,利用图4(b)电路进行分析,计算简便,而且也能较好地近似反映实际情况[1]。
3 结语
(1)本文通过举例说明,电容电压和电感电流的跃变可以在多种情况下发生,而不仅限于一般教科书所指出的两种情形。值得注意的是,采用时域法分析动态电路时,分析的起点是t=0+时刻,此时应注意电容电压和电感电流的跃变问题;而采用拉氏变换分析动态电路时,分析的起点是t=0-时刻,分析过程避开了电容电压和电感电流的跃变问题。因此,采用拉氏变换分析动态电路更有优势。
(2)对实际电路而言,换路定律成立。电容电压和电感电流的跃变是对实际电路理想化建模所出现的情况。在教学中应正确认识两者之间的关系。
(3)正确理解电容电压和电感电流的跃变,有助于简化电路的分析。
[1]李瀚荪.简明电路分析基础[M].北京:高等教育出版社.2002
[2]陈希有.电路理论教程[M].北京:高等教育出版社.2013
[3]孙玉坤,陈晓平.电路原理[M].北京:机械出版社.2006
