基于GLC-KSVD的稀疏表示人脸识别算法

封 睿，李小霞

(西南科技大学 信息工程学院，四川 绵阳 621010)

自动人脸识别技术一直是计算机视觉、机器学习和生物识别领域中具有挑战性的研究课题。2009 年Wright 等［1］提出将稀疏表示理论应用到人脸识别技术中，该方法对光照、遮挡、伪装有较好的鲁棒性。基于稀疏表示的图像分类(sparse representation classification，SRC)首先用训练样本构造一个超完备字典，将待测样本用字典原子的稀疏线性组合来表示，然后通过待测样本的稀疏编码系数实现分类。

稀疏编码的效果取决于字典的质量。Wright 等用整个训练样本集构造字典，在实践中为了获得好的分类效果通常需要大规模的训练样本集，导致计算量很大。近年来，国内外学者基于字典学习的思想，提出许多能够表示给定信号的更加紧凑的小型字典学习算法，取得了较好的分类效果。2006 年Aharon 等［2］提出K-SVD 字典学习算法，得到的新字典能够很好地表示训练样本，但是没有考虑字典的判别性。文献［3-6］将稀疏系数作为图像的特征，在字典学习的基础上训练分类器，这些方法将字典学习和分类器设计分开进行，得到的新字典对于分类不是最优的。另外，一些学者通过增加字典的约束条件，得到判别性字典和分类器。2008 年Pham 等［7］在K-SVD 算法中增加了分类误差约束条件，该算法将字典更新和预测分类器设计过程交替迭代，得到了更利于分类的新字典，但是只能得到一个局部最优解。2010 年张等［8］提出判别性KSVD(DKSVD)算法，同时得到全局最优的判别性字典和线性预测分类器，但是在字典较小的情况下不能保证稀疏系数的判别性。2010 年杨等［9］对每一个类别分别进行字典学习和分类器设计，但是该算法在类别多的情况下十分耗时。2013 年胡等［10］通过Fisher 判别准则约束稀疏系数，得到具有判别性的新字典，但是不适于类别多的情况。

为了减小稀疏编码的计算量，通常需要通过特征提取对原始图像进行降维，常采用下采样、Eigenface、Fisherface 及随机投影等方法来提取图像的整体特征。文献［1］表明在特征维数足够高的情况下，SRC 算法对整体特征不敏感，即使是随机投影都能达到较好的识别效果，但是实践中训练样本的数量往往是有限的，而整体特征容易受到光照、表情、姿态、局部变形等影响，不能很好的表示样本。Gabor 滤波器能够有效地提取图像在多个方向、多个尺度上的局部特征，并被成功的应用到人脸识别技术中［11-14］，从图像的局部区域提取的Gabor 特征对光照、表情和姿态等都有更强的鲁棒性。

考虑字典学习在稀疏表示图像识别中的作用以及Gabor特征对光照、表情和姿态的鲁棒性，本文提出一种基于Gabor特征和标签一致字典学习的GLC-KSVD 稀疏表示人脸识别算法。首先提取样本多尺度多方向的Gabor 特征，将训练样本的Gabor 特征矩阵作为初始特征字典，然后通过字典学习同时得到全局最优的判别性字典和线性分类器。学习到的新字典能够很好的对信号进行稀疏表示，并且对于任意大小的字典，编码系数都具有很强的判别性，来自同一类别的样本具有相似的稀疏系数，通过一个简单的线性分类器就能达到较好的识别性能，同时也减小了计算代价。

1 字典学习

字典学习是为了从样本中学习一个能够更好地表示或编码给定信号的一组基。令Y=［y1…yN］∈Rn×N表示N 个n维输入信号，则字典学习模型表示为:

式(1)中，D =［d1，d2，…，dk］∈Rn×k是学习到的字典，X =［x1，x2，…，xN］∈Rk×N是输入信号Y 的稀疏系数矩阵，T 是稀疏约束因子，‖Y-DX‖表示重构误差。

K-SVD 算法通过迭代求解式(1)，同时得到重构字典D和稀疏系数矩阵X，但是仅考虑了对给定信号的重构性，不利于分类。

2 基于GLC-KSVD 的人脸识别算法

2.1 Gabor 纹理特征集

Gabor 核函数表示为

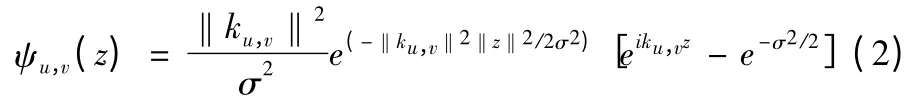
式(2)中，μ 和ν 分别是滤波器的方向和尺度因子，z =(x，y)表示像素，kμ，ν=kνeiφμ，kν=kmax/fν，φμ=πμ/8，kmax是最大采样频率，f 是采样步长，σ 是高斯函数方差。

选取5 个尺度和8 个方向构造Gabor 滤波器组，然后分别与人脸图像进行卷积提取Gabor 特征。令I(x，y)表示人脸图像，将其与Gabor 核函数进行卷积可得:

式(3)中，Gu，v(z)是复数，其幅值包含了图像局部能量的变化，用来描述图像的特征。每幅图像分别与40 个Gabor 滤波器进行卷积，然后对每个幅值矩阵进行下采样、向量化，最后将这40 个列向量连接起来，构成增广Gabor 纹理特征向量:

2.2 GLC-KSVD 算法

基于GLC-KSVD 的人脸识别算法用训练样本的Gabor特征向量χ 代替公式(1)中的原始训练样本Y，构成Gabor 纹理特征集G=χ(Y)=［χ(y1)，χ(y2)，…，χ(yN)］。GLC-KSVD算法在字典学习模型中加入标签一致约束条件，再通过KSVD 算法得到一个同时具有重构性和判别性的字典。下面分别在式(1)中加入标签一致正则项(GLC-KSVD1)及结合标签一致和分类误差的正则项(GLC-KSVD2)。

2.2.1 GLC-KSVD1 算法

一个线性分类器的性能取决于输入的稀疏系数的判别性。为了在字典D 上得到具有判别性的稀疏系数，在式(1)中加入标签一致正则项，GLC-KSVD1 字典学习模型为

式(5)中，α 是正则化参数，Q=［q1，q2，…，qN］∈RK×N是输入信号G 的判别式稀疏系数矩阵，A 是线性变换矩阵，‖Q-AX‖表示判别式稀疏编码误差。假设G =［χ1，χ2，…，χ6］，D =［d1，d2，…，d4］，其中χ1、χ2、χ3、d1、d2属于类别1，χ4、χ5、χ6、d3、d4属于类别2，那么

稀疏编码误差项使编码系数在任意字典大小下都具有很强的判别性，来自同一类别的信号具有相似的稀疏表示，不需要对每个类别进行分类器学习，只需要一个简单的线性分类器就能达到良好的分类性能，同时减小了计算成本。

2.2.2 GLC-KSVD2 算法

为了得到更好的分类性能，在式(5)中加入分类误差项，GLC-KSVD2 字典学习模型为

式(6)中，α、β 是正则化参数，H 是输入信号G 的类别矩阵，W 是线性分类器参数，‖H-WX‖22 表示分类误差，它使分类器更利于分类。

2.2.3 GLC-KSVD 最优化问题

下面介绍GLC-KSVD2 的最优化求解方法，GLC-KSVD1可以使用相似的方法，GLC-KSVD2 最优化求解模型表示为

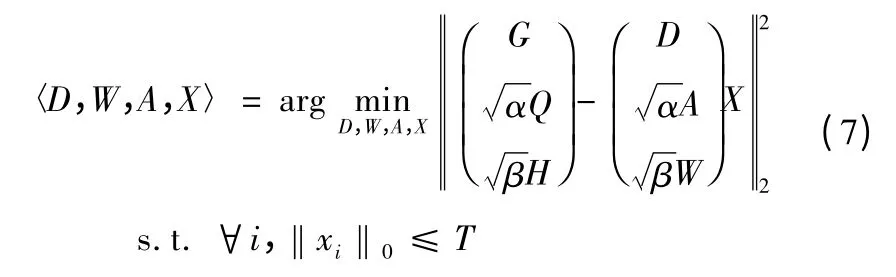
然后，通过K-SVD 算法求得Dnew和X，从而得到D、A、W。GLC-KSVD 算法同时求得D、A、W 的值，解决了局部最优的问题，适用于小字典、类别多的情况，也便于加入其他的判别项。

图1 显示了两个不同的人脸库中，某一类测试样本在不同字典上的稀疏系数，X 轴表示稀疏系数的维度，Y 轴表示这类测试样本的稀疏系数的绝对值之和。第一列曲线对应Extended YaleB 人脸库的第2 个人(含32 个测试样本)，第二列曲线对应AR 人脸库的第89 个人(含6 个测试样本)。图1(f)和(g)颜色条中的每种颜色代表字典原子的一个类。

不同于K-SVD 和DKSVD，在GLC-KSVD 和SRC、SRC*算法中字典原子和类别标签相对应，由图1(f)和图1(g)可以看出GLC-KSVD 使来自同一类别的样本具有相似的稀疏表示，与测试样本同一类别的字典原子对其稀疏编码的贡献显著高于其他的字典原子。稀疏系数的这种判别性对于提高线性分类器的性能十分重要。

2.3 初始化

在GLC-KSVD 算法中，首先需要初始化参数D0、A0和W0。对每一类别分别进行K-SVD 字典学习，然后合并所有学习到的字典来初始化D0，其中每一类字典原子的数目是一致的，每个原子dk的类别标签被初始化为相应的类别号，且在整个算法中保持不变。初始化D0后，求解G 的稀疏系数矩阵X，然后通过多元回归模型来初始化A0和W0，计算公式为

图1 采用不同稀疏编码方法的稀疏系数示例

2.4 分类

通过K-SVD 算法求得Dnew，从而得到D = {d1，d2，…，dK}、A={a1，a2，…，aK}、W={w1，w2，…，wK}，因为Dnew的每一列是归一化的，所以在测试过程中需要对D、A、W 进行转化:

对于测试图像yi，首先计算出χ(yi)相应的稀疏系数xi:

然后通过线性预测分类器来估计yi的类别:

3 实验仿真

为了检验本文算法的有效性，在Extended YaleB 人脸库和AR 人脸库上分别进行实验，实验平台为酷睿2 双核处理器，主频2.93 GHz，2 GB 内存。为了保证结果的准确性，实验结果为独立运行10 次后的平均识别率和运行时间。

3.1 Extended YaleB 数据库

Extended YaleB 人脸库共有38 个人，每个人有64 幅正面人脸图像，包括光照和表情变化。对于每个人，随机选择32 幅用于训练，其余的用于测试。所有图像的尺寸归一化到192 ×168 像素，经随机投影后特征维数降到504 维，学习到的字典包含570 个原子，每人15 个。不同于K-SVD 和DKSVD，GLC-KSVD 和SRC 一样，其字典原子和类别标签相对应，对于SRC 实验选择全体训练样本和每人15 幅图像两种不同的字典，所有的方法使用相同的学习参数。

表1 列出了本文算法和K-SVD、DKSVD、SRC 及采用相同字典大小的SRC* 的识别率。大多数的错误识别是因为图片的光线太暗，参照文献［11］剔除质量很差的图片(每人约10 幅)，进行了另外一组实验，实验结果列在表1 第3 行。

表1 Extended YaleB 上不同方法的识别率 %

由表1 可以看出本文算法的识别率高于K-SVD、DKSVD，且明显高于采用相同字典大小的SRC* ，GLC-KSVD2 的识别率高于GLC-KSVD1。在原图库上GLC-KSVD 达到了96.3%的最高识别率，略低于SRC 的识别率。剔除质量很差的图片后，GLC-KSVD 达到了99.2%的最高识别率，略高于SRC 的识别率。

表2 列出了本文算法和SRC、SRC*识别一个样本的平均运行时间，可以看出采用小字典的SRC*、GLC-KSVD1 及GLC-KSVD2 的运行速度比SRC 快，并且本文算法的运行速度比SRC 提高11.9 倍，比选择相同字典大小的SRC*提高6 倍。

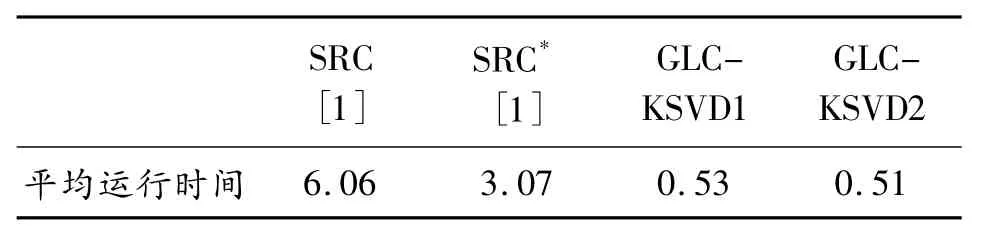
表2 Extended YaleB 上不同方法的平均运行时间 ms

3.2 AR 数据库

AR 人脸库共有126 个人，每个人有26 幅正面人脸图像，包括光照、表情和伪装变化。从中选取50 名男性和50名女性的2 600 幅图像用于实验，对于每个人，随机选择20幅用于训练，另外6 幅用于测试。所有图像的尺寸归一化到165 ×120 像素，经随机投影后特征维数降到540 维，学习到的字典包含500 个原子，每人5 个。对于SRC 实验选择两种不同大小的字典。

表3 列出了本文算法和K-SVD、DKSVD、SRC 及采用相同字典大小的SRC* 的识别率。由表3 可以看出本文算法的识别率明显高于K-SVD、DKSVD 及SRC* ，并且由于AR库中人脸图像存在光照、表情、伪装等变化，GLC-KSVD 的识别率高于单纯采用随机投影的SRC，达到了97.7%。

表3 AR 库上不同方法的识别率 %

表4 列出了本文算法和SRC、SRC* 识别一个样本的平均运行时间，可以看出SRC*、GLC-KSVD1 及GLC-KSVD2 的运行速度比SRC 快，并且本文算法的运行速度比SRC 提高41.9 倍，比采用相同字典大小的SRC*提高11.4 倍。

表4 AR 库上不同方法的平均运行时间 ms

由实验结果看出对于一个包含大量训练样本的数据库，与用整个训练样本集作字典相比，学习一个小字典可以节省很多时间。GLC-KSVD 算法使稀疏系数具有判别性，只用一个简单的线性分类器就达到了最好的识别率，同时大大提高了运行速度，尤其是在类别多的情况下，运行速度提高更多。

4 结论

本文提出基于Gabor 特征和标签一致字典学习的GLCKSVD 稀疏表示人脸识别算法，提取训练样本的Gabor 特征来构建初始特征字典，对光照、表情、姿态、伪装等有更强的鲁棒性。GLC-KSVD1 通过综合重建误差、稀疏编码误差，使编码系数在任意字典大小下都具有很强的判别性，来自同一类别的信号具有相似的稀疏表示，不需要对每个类别分别进行复杂的分类器学习，通过一个简单的线性分类器就达到了良好的分类性能，也减小了计算成本。GLC-KSVD2 通过综合重建误差、稀疏编码误差和分类误差，使稀疏系数更利于分类。GLC-KSVD 还通过最优化求解方法，得到了全局最优的判别性字典和线性分类器，也便于加入其他的判别项。实验结果表明，本文算法达到了较好的识别效果，适用于小字典，对表情、伪装、姿态变化等有更强的鲁棒性，且运行速度大大提高，尤其是在类别多的情况下，运行速度提高更多。

［1］WRIGHT J，YANG A Y，GANESH A，et al. Robust face recognition via sparse representation［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，2009，31（2）:210-227.

［2］AHARON M，ELAD M，BRUCKSTEIN A.K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation［J］. IEEE Transactions on Signal Processing，2006，54（1）:4311-4322.

［3］MAIRAL M，LEORDEANU M，BACH F，et al.Discriminative sparse image models for class-specific edge detection and image interpretation［C］//Proceedings of the 10th European Conference on Computer Vision. Marseille，France:Springer，2008:43-56.

［4］ZHANG W，SURVE A，FEM X，et al.Learning non-redundant codebooks for classifying complex objects［C］//Proceedings of the 26th Annual International Conference on Machine Learning. New York，USA: ACM，2009: 1241-1248.

［5］BOUREAU Y L，BACH F，LECUM Y，et al.Learning midlevel features for recognition［C］//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco，CA，USA: IEEE Computer Society，2010:2559-2566.

［6］MAIRAL J，BACH F，PONCE J，et al.Discriminative learned dictionaries for local image analysis［C］//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Anchorage，AK，USA: IEEE Computer Society，2008:1-8.

［7］PHAM D，VENKATESH S. Joint learning and dictionary construction for pattern recognition［C］//proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Anchorage，AK，USA: IEEE Computer Society，2008:1-8.

［8］ZHANG Q，LI B X. Discriminative K-SVD for dictionary learning in face recognition［C］//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. San Francisco，CA，USA: IEEE Computer Society，2010:2691-2698.

［9］YANG J，YU K，HUANG T.Supervised translation-invariant sparse coding［C］//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition.San Francisco，CA，USA: IEEE Computer Society，2010:3517-3524.

［10］胡正平，徐波，白洋.Gabor 特征集结合判别式字典学习的稀疏表示图像识别［J］.中国图象图形学报，2013，18（2）:189-194.

［11］JIANG Z L，LIN Z，DAVIS L S.Learning a discriminative dictionary for sparse coding via label consistent K-SVD［C］//Proceedings of IEEE Computer Society Conference on Computer Vision and Pattern Recognition. Providence，RI，USA:IEEE Computer Society，2011:1697-1704.

［12］张文超，山世光，张洪明，等.基于局部Gabor 变化直方图序列的人脸描述与识别［J］.软件学报，2006，17（12）:2508-2517.

［13］YANG M，ZHANG L.Gabor feature based sparse representation for face recognition with Gabor occlusion dictionary［C］//Proceedings of the 11th European Conference on Computer Vision.Crete，Greece:Springer，2010:448-461.

［14］张娟，占永照，毛启容，等.基于Gabor 小波和稀疏表示的人脸表情识别［J］. 计算机工程，2012，38（6）: 207-212.