带有反馈控制的单种群系统的持久性与一致渐近稳定性

杨永燕，付宏睿

（安阳师范学院人文管理学院数学与信息工程系，河南安阳455000）

带有反馈控制的单种群系统的持久性与一致渐近稳定性

杨永燕，付宏睿

（安阳师范学院人文管理学院数学与信息工程系，河南安阳455000）

研究带有反馈控制的离散单种群系统的持久性，并通过构造一个李雅普诺夫函数来证明这个系统是一致渐近稳定的.

反馈控制；持久性；一致渐近稳定性

0 引言

最近许多学者把单种群系统应用到了经济领域，［1—3］作者Belair和Mackey假设市场价格的相对变化是由方程＝f（P，P）来决定的.DS在这个模型中，PD和PS分别表示商品的需求和供给价格，它的一个特例为其中a，b，c，d，τ，m∈（0，∞），n∈［1，∞）.在［4］中，作者研究了这个系统的解的存在唯一性、有界性及振荡性.

如果n＝0，方程（1.1）可转换为

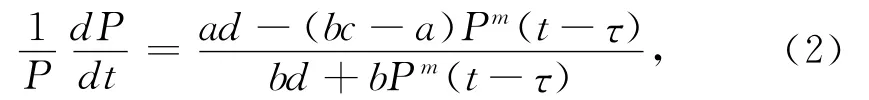
当ad＝bd＝K和bc—a＝A是常数时，方程（2）称为食物有限的种群模型，在文章［5］、［6］中作者研究了这个模型的正解的振荡性、全局吸引性.

但事实上，生态系统会由于外界的干扰使种群生存率产生变化，即模型中的参数会改变.所以，研究控制变量即干扰函数的模型是很有必要的.近年来，不少学者研究了差分方程在种群模型中的应用.［7—8］带有反馈控制的单种群和多钟群模型的动态学行为也是许多学者的研究方向.［9—10］

许多学者认为，由差分方程产生的离散时间模型比连续的模型更实际，而且也能为连续模型提供有效的计算模型.因此，离散系统的动态学成了许多学者的研究对象.［10—11］在文献［12］的启发下，得到了带有反馈控制的离散系统如下：

（H1）c（n），α（n），β（n）是有界非负概周期序列，

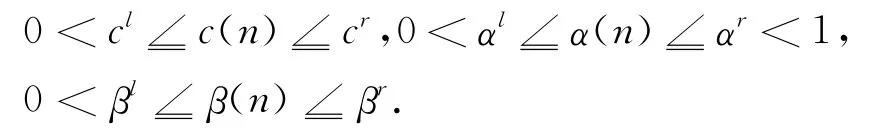
根据对现实的考虑，只研究这个系统的正解.所以系统（3）的初始条件为

不难看出，对于所有的n∈ℤ+，系统（3）的解是良定义的，且满足x（n）＞0，u（n）＞0.

1 预备知识

定义1.1［13］一个序列x：ℤ→ℝ称为概周期序列，如果x的ε移位数集有以下性质：

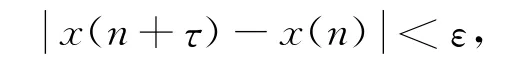
则τ称为x（n）的ε概周期.

定义1.2［13］令f：×D→ℝ，其中D是ℝ上的开集，f（n，x）对于x∈D关于n是一致概周期的，如果对于任给的ε＞0和D中任意的紧集S，存在一个正整数l（ε，S），使得ℝ的长度为l的任意区间l（ε，S）内总有τ使

引理1.1［13］x（n）是一个概周期序列当且仅当对于任意的⊂都存在一个子序列hk⊂使得当n∈且k→∞时，x（n+hk）一致收敛.且这个有限序列也是一个概周期序列.

定理1.1［14］假设存在一个定义在n∈上的李雅普诺夫函数V（n，x，y），‖x‖＜B，‖y‖＜B，满足以下条件：

（c）ΔV（2.2）（n，x，y）≤—λV（n，x，y），其中0＜λ＜1是一个常数，ΔV（2.2）（n，x，y）＝V（n+1，f（n，x），f（n，y）—V（n，x，y）.

2 系统的持久性与一致渐近稳定性

引理2.1 假设条件（H1）成立且f（n，x）关于x是非增的，）是有界的.同时假设）是系统（3）的正平衡点，且

那么存在M1，M2＞0使得每个解x（n）和u（n）满足

证明：由系统（3），可证得当x（n）存在时，下面的式子成立：

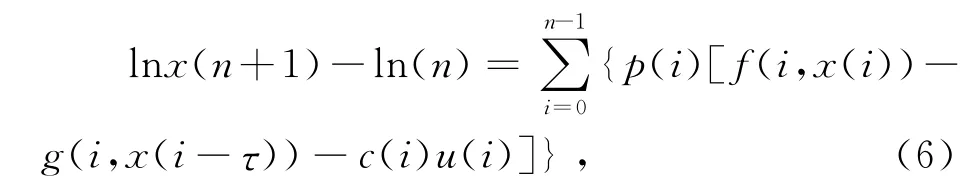
其中i∈ℤ+，并且只要x（i）存在，则是被唯一定义且是正的.

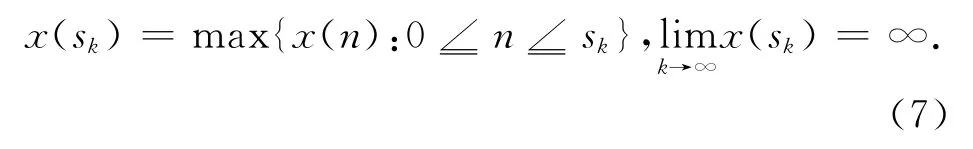
由系统（3），可以得到f（sk，x（sk））—g（sk，x（sk—τ））—c（sk）u（sk）≥0，因此可以导出f（sk，x（sk））≥g（sk—τ，x（sk—τ））+c（sk）u（sk）.由方程（7）易知x（sk—τ）≤x（sk）.因为f是非增的，所以可得出

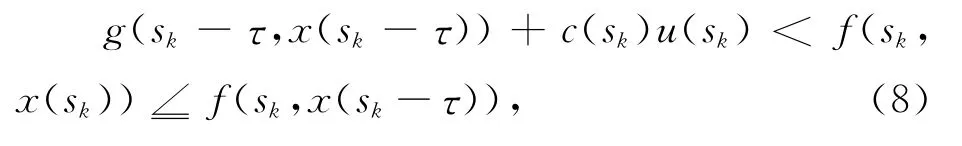
结合（5）可得x（sk—τ）≤，n＝0，1，…，进而由系统（3）可得

显然，当k→∞时，上式的左侧趋于无穷，根据f的非增性质，不等式的右侧是有界的.所以产

生矛盾.因此，存在M1＞0使得M1.显然，同样可以证明对于任意的n∈，系统（3）的解x（n），n∈是存在的.接下来证明存在M2＞0使得

对于任意的ε＞0，存在一个足够大的整数n0∈使得x（n）≤M1+ε，n≥n0.

因为0＜αl＜1，我们可以找到一个正数d使得1—αl＝e—d，应用Stolz’s定理可以得到

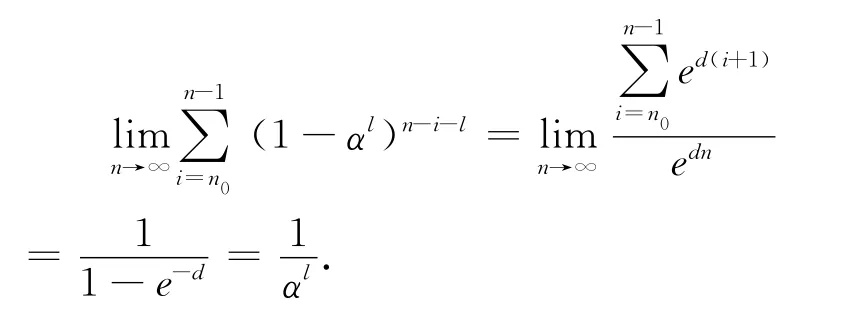
引理2.2 假设条件（H1）成立，并且满足引理2.1的条件，那么存在m1，m2＞0使得成立.

证明类似于引理2.1的证明.

定理2.1 如果引理2.1与引理2.2成立，则系统（3）是持久的.

注：由定理2.1可以直接看出反馈控制对于商品模型或者生物模型的持久性是没有危害的.

定义Ω为系统（3）包含所有解（x（n），u（n））的集合，即Ω＝｛（x（n），u（n））|m1≤x（n）≤M1，m2≤u（n）≤M2，n∈｝.从引理2.1、引理2.2及定理2.3可知，Ω是系统（3）的不变集.

定理2.2 假设引理2.1的条件成立，并且f和g关于n是概周期的，（x，u）是关于n的有界周期解，那么Ω≠.

证明：由f（n，x），g（n，x），c（n），α（n），β（n），p（n）的概周期性，存在一个整数序列τξ，τξ→∞，ξ→∞，使得

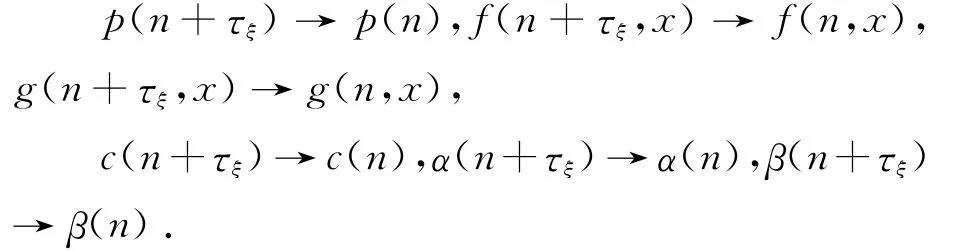
令ε是任意小的正数，由引理2.1和引理2.2可知，存在一个正整数N0，使得

当n≥N0—τξ，（ξ＝1，2，…）时，记xξ（n）＝x（n+τξ），uξ（n）＝u（n+τξ）.对于任意的正整数q，很容易知道，存在序列｛xξ（n）：ξ≥q｝和｛uξ（n）：ξ≥q｝使得在任意一个的有限区间上，当ξ→∞时，序列xξ（n）和uξ（n）存在子序列，xξ（n）和uξ（n）收敛.因此，有序列y（n）和v（n）使得任意的n，当p→∞时，xξ（n）→y（n），uξ（n）→v（n）.结合下式

可得

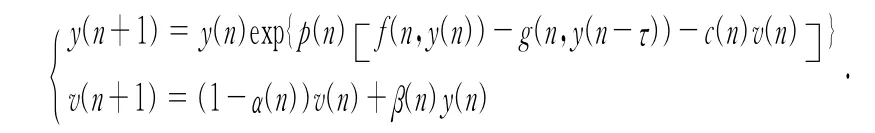
因此（y（n），v（n））是系统（3）的一个解，且m1—ε≤y（n）≤M1+ε，m2—ε≤v（n）≤M2+ ε，n∈.因为ε是任意小的正数，有m1≤y（n）≤M1，m2≤v（n）≤M2，n∈成立.故Ω≠.

定理2.3 假设条件（H1）成立，且f，g是L—利普希兹的，且利普希兹系数分别是L1，L2，对于任意的n∈ℤ+，p（n）≤p0，且满足

（H2）0＜Θ＜1，其中Θ＝min｛Θ1，Θ2｝，且

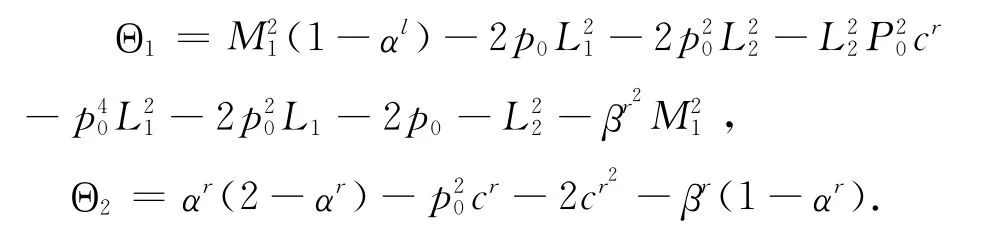
那么存在唯一一个一致渐近稳定的概周期解集X＝（x（n），u（n）），使得当n∈时，m1≤x（n）≤M1，m2≤u（n）≤M2.

证明：令y（n）＝lnx（n），由系统（3）可知

由定理2.2可知系统（10）存在一个有界解lnm1≤y（n）≤lnM1，m2≤u（n）≤M2，n∈ℤ+.因此，，其中A＝

对于（y，u）∈ℝ2，我们定义范数‖（y，u）‖假设X＝（y（n），u（n）），Y＝（z（n），v（n））是系统（10）定义在ℤ+×Ω＊×Ω＊的任意两个解，那么‖X‖≤C，‖Y‖≤C，其中C＝A+B，

考虑系统（10）的积系统

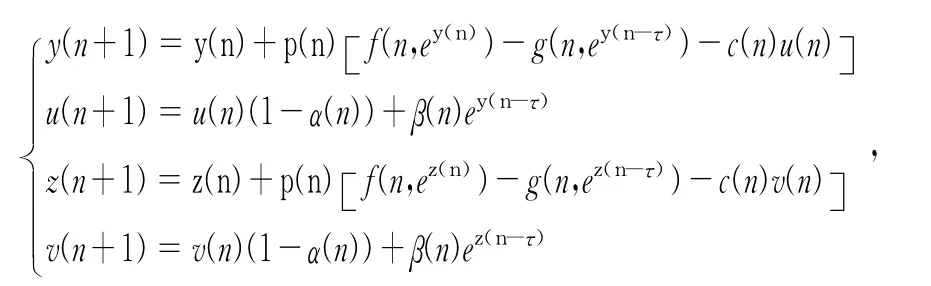
可以在ℤ+×Ω＊×Ω＊上定义李雅普诺夫函数V（n，X，Y）＝（y（n）—z（n））2+（u（n）—v（n））2.容易验证范数‖X—Y‖＝|y（n）—z（n）|+| u（n）—v（n）|与‖X—Y‖＊＝［（y（n）—z（n））2+（u（n）—v（n））2］是等价的，即存在两个常数C1＞0，C2＞0使得C1‖X—Y‖≤‖X—Y‖＊≤C2‖X—Y‖，因此（C1‖X—Y‖）2≤V（n，X，Y）≤（C2‖X—Y‖）2.

令a，b∈C（ℝ+，ℝ+），a（x）＝x2，b（x）＝x2，所以定理1.1的条件（a）是成立的.此外，

ΔV（n，X，Y）＝V（n+1，X，Y）—V（n，X，Y）（u（n）—v（n））2］＝—ΘV（n，X，Y）.对于0＜Θ＜1，定理1.1中的条件（c）成立，即定理1.1中所有条件都成立，所以系统（10）存在唯一一个一致渐近稳定的概周期解，故系统（3）存在一个一致渐近稳定的概周期解X＝（x（n），u（n）），当n∈时满足m1≤x（n）≤M1，m2≤u（n）≤M2.

［1］C.Qian.Global attractivity in a delay differential equation with application in a commodity model［J］.Appl. Math.Lett，2010（5）：127—136.

［2］J.Beiair，M.C.Mackey.Consumer memory and price fluctuations in a commodity market：an integrodifferential model［J］.J.Dynam.Diff.Equation，1989（3）：299—325.

［3］M.C.Mackey.Commodity price fluctuations：price dependent delays and nonlinearities as explanatory factors［J］.Econ.Theory，1989（48）：497—508.

［4］A.M.Farahani，E.A.Grove.A simple model for price fluctuations in a single commodity market［J］.Contemp，Math，1992（31）：97—103.

［5］K.Gopalsamy，M.R.S.Kulenovic，G.Ladas.Time lags in a foodlimited population model［J］.Appl.Anal，1988（31）：225—237.

［6］E.A.Grove，G.Ladas，C.Qian.Global attractivity in a“food—limited”population model［J］.Dynam Systems Appl，1993（2）：243—250.

［7］P.Cull.Local and global stability for population models［J］.Biol.Cybernet，1986（54）：141—149.

［8］E.M.Elabbasy，S.H.Saker.Periodic solutions and oscillation of discrete nonlinear delay population dynamics mod—el with external force［J］.IMAJ.Appl.Math，2005（70）：753—767.

［9］X.X.Chen，F.D.Chen.Stable periodic solution of a discrete periodic Lotka—Volterra competition system with a feedback control［J］.Appl Math Comput，2006（181）：1446—1454.

［10］X.Li，M.Fan，Wang Ke.Positive periodic solution of single species model with feedback regulation and infinite delay［J］.Appl Math J Chinese Univ Ser A，2002（1）：13—21.

［11］Li YK，Lu LH.Positive periodic solutions of discrete n—species food—chain systems［J］.Appl.Math.Comput，2005（167）：324—44.

［12］Li YK.Global stability and existence of periodic solutions of discrete delayed cellular neural networks［J］.Phys Lett A，2004（333）：51—61.

［13］Zhang TW，Li YK，Ye.Persistence and almost periodic solutions for a discrete fishing model with feedback control［J］.Commun Noninear Sci Numer Simulat，2010（2）：97—101.

［14］David C，Cristina M.Invariant manifolds，global attractors and almost periodic solutions of nonautonomous deffer—ence equations［J］.Nonlinear Anal，2004（44）：465-484.

［15］X.JB，Zhidong Teng.Permanence for a nonautonomous discrete single—species system with delays and feedback control［J］.Appl.Math.Lett，2010（11）：949—954.

［责任编辑 范 藻］

Permanence and Uniformly Asymptotic Stability in a Discrete Single—Species System with Feedback Control

YANG Yong—yan，FU Hong—rui

（HumanisticManagement College of Anyang Normal University，Anyang Henan455000，China）

In this thesis，firstly consider the following discrete single—species system with delay and feedback control. We establish the sufficient conditions for the persistence and by constructing a Lyapunov function to prove the uniformly asymptotic stability of the above system.

feedback control；permanence；asymptotic stability

O175

A

1674—5248（2014）05—0010—05

2014—03—25

杨永燕（1985—），女，河南安阳人.助教，硕士，主要从事微分方程研究.